每日一题：1483. 树节点的第 K 个祖先

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

• TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
• getKthAncestor(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

示例 1：

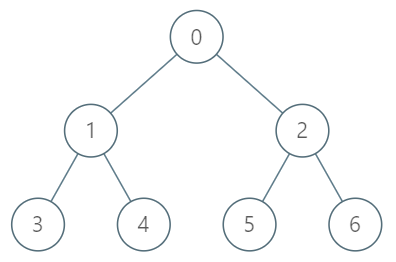
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

思路：开始以为很简单，只要在parent数组上不停回溯就好了，但最终在n=5000时超时了……

class TreeAncestor {
public:
    vector<int> p;
    TreeAncestor(int n, vector<int>& parent) {
        p.resize(n);
        for(int i=0;i<n;i++){
            p[i]=parent[i];
        }
    }
    
    int getKthAncestor(int node, int k) {
        for(int i=1;i<=k;i++){
            if(p[node]!=-1)node=p[node];
            else return -1;
        }
        return node;
    }
};

超时原因是每次只能一步一步跳，如果能优化成一次跳两步或是四步，就能快很多了，而如何维护一个节点的第2ⁱ个节点呢？这里用一个新学到的倍增（Binary Lifting）的方法：

class TreeAncestor {
    vector<vector<int>> pa;
public:
    TreeAncestor(int n, vector<int> &parent) {
        int m = 32 - __builtin_clz(n); // n 的二进制长度
        pa.resize(n, vector<int>(m, -1));
        for (int i = 0; i < n; i++)
            pa[i][0] = parent[i];
        for (int i = 0; i < m - 1; i++)
            for (int x = 0; x < n; x++)
                if (int p = pa[x][i]; p != -1)
                    pa[x][i + 1] = pa[p][i];                //eg：若x的第2个祖先节点是p，则p的第2个祖先节点是x的第4个祖先节点
    }

    int getKthAncestor(int node, int k) {
        int m = 32 - __builtin_clz(k); // k 的二进制长度
        for (int i = 0; i < m; i++) {
            if ((k >> i) & 1) { // k 的二进制从低到高第 i 位是 1
                node = pa[node][i];
                if (node < 0) break;
            }
        }
        return node;
    }

    // 另一种写法，不断去掉 k 的最低位的 1
    int getKthAncestor2(int node, int k) {
        for (; k && node != -1; k &= k - 1) // 也可以写成 ~node
            node = pa[node][__builtin_ctz(k)];
        return node;
    }
};

作者：灵茶山艾府
链接：https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/solutions/2305895/mo-ban-jiang-jie-shu-shang-bei-zeng-suan-v3rw/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。