每日一题： 2192. 有向无环图中一个节点的所有祖先

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

示例 1：

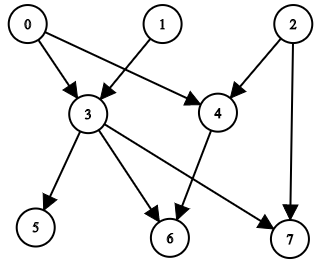
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。

本题是一个图论问题，本质是拓扑排序，我还以为要用并查集来做，事实上这个思路是不完全正确的。该问题必须用已知答案来推出未知答案，而我最开始默认0一定是入度为0的点，即父节点是确定的（没有父节点），但通过样例发现并非这样，因此就陷入如何选择起点的问题，当我试图再找一个入度为0的点作为起点时，发现仅靠发现一个起点并不能解决所有问题，因为无论从哪里出发，我的思路都不能保证递归做合并父节点集合的时候父节点集合是确定的，因此也只是通过了部分样例。

class Solution {
public:
    void merge(const vector<vector<int>>& fa,set<int>& son,int index){    //将查找i节点的父节点
        son.insert(index);
        for(int i:fa[index]){
            son.insert(i);
            merge(fa,son,i);
        }
    }
    void print(const set<int>& tmp,vector<int>& result){                //将集合set并入对应i节点的父节点集合
        for(int i:tmp)result.push_back(i);
    }                                        
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
        vector<vector<int>> result(n);
        int start=0;
        for(int k=0;k<n;k++){                                        //尝试寻找一个入度为0的作为起点
            int flag=0;
            for(int i=0;i<edges.size();i++)if(edges[i][1]==k){flag=1;break;}
            if(!flag){
                start=k;break;
            }
        }
        set<int> tmp;
        int flag=1;
        for(int i=start;flag||i%n!=start;i+=1,i%=n){
            flag=0;
            for(int j=0;j<edges.size();j++){
                if(edges[j][1]==i)merge(result,tmp,edges[j][0]);
            }
            print(tmp,result[i]);
            tmp.clear();
        }
        return result;
    }
};

 正确做法，利用拓扑序列的思路，先处理入度为0的，然后是将处理过的“删除”，继续处理新的入度为0的节点：

class Solution {
public:
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n, vector<int>());
        vector<set<int>> ans(n);
        vector<int> in(n, 0);
        for(auto e : edges){
            int x = e[0], y = e[1];
            g[x].push_back(y);
            in[y]++;
        }
        queue<int> q;
        for(int i = 0; i < n; i++){
            if(in[i] == 0) q.push(i);
        }
        while(!q.empty()){
            int u = q.front();
            q.pop();
            for(auto v : g[u]){
                ans[v].insert(u);
                for(auto x : ans[u]) ans[v].insert(x);
                if(--in[v] == 0) q.push(v);
            }
        }
        vector<vector<int>> res(n);
        for(int i = 0; i < n; i++) res[i] = vector<int>(ans[i].begin(), ans[i].end());
        return res;
    }
};

作者：实名吃香菜
链接：https://leetcode.cn/problems/all-ancestors-of-a-node-in-a-directed-acyclic-graph/solutions/2723576/tuo-bu-pai-xu-by-xinpengq-2132/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。