Day 1
A. fibonacci
题目描述
令 \(S_0=\tt a\),\(S_1=\tt b\),定义斐波那契串 \(S_i=S_{i-1}+S_{i-2}\),加号表示拼接。
给定一个字符串 \(t\),仅由字母 \(\tt ab\) 构成,求 \(S_{\infty}\) 最短的一个子串满足 \(t\) 是该子串的子序列,输出该子串长度。
\(1\le|t|\le1.5\times10^5\)。
题目分析
首先答案一定不超过 \(3n\),因为生成的串不存在超过 \(2\) 个的连续相同字符,其次这个串也不需要生成很长,\(10^6\) 量级足矣。
然后考虑一件很厉害的事情,将 \(S\) 按照拼接方式劈开,得到一个类似线段树的结构:
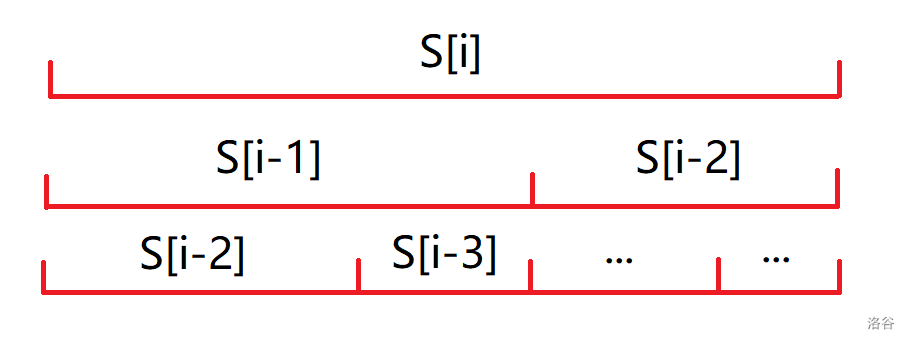
预处理 \(f[i][j]\) 表示当前 \(t\) 已经匹配了 \(i\) 位,再拿去和 \(S_j\) 匹配之后能匹配到第几位,处理方式和倍增类似。
然后我们就得到了一个 \(O(\log n)\) 判断 \(t\) 是否是 \(S\) 某个子串的子序列的方法:类似线段树那样拆成 \(O(\log n)\) 段小的 \(S_i\),每段利用上面预处理的那个数组向后匹配。
直接双指针扫描所有极短的 \(t\) 可匹配的子区间即可,时间复杂度 \(O(n\log n)\)。
代码
B. tap
题目描述
平面上有 \(n\) 条线段,第 \(i\) 条线段两个端点分别为 \((l_i,h_i)\) 和 \((r_i,h_i)\),且每个线段中点上方 \(0.5\) 个单位处有个水龙头。
打开某个线段的水龙头后,水会沿着这条线段两端流下去,流到地板或下一条线段,且流到下一条线段后会继续流。
按随机顺序打开水龙头,每次在没有水的线段中等概率选一个打开,问期望打开几次使所有线段有水。
\(1\le n\le 5\times 10^5\),\(\{l_i,r_i\}\) 构成 \(1\) 到 \(2n\) 的排列,\(h_i=i\)。
题目分析
考虑 \(O(n^2)\) 做法,我们将每个线段与两个端点向下延长第一个碰到的线段分别连边,这样会连出来一个 DAG。
转化下期望,根据期望的线性性等于求每个点被选到的概率之和,而一个点如果被选那么此时所有能到达该点的其他点一定都没有被选,也就是设算上点 \(i\) 能到达 \(i\) 的点有 \(C_i\) 个,那么答案就是 \(\sum\frac{1}{C_i}\),可以类比一道叫 Game on Tree 的题。
继续优化需要一个观察,上一下课件里的图:
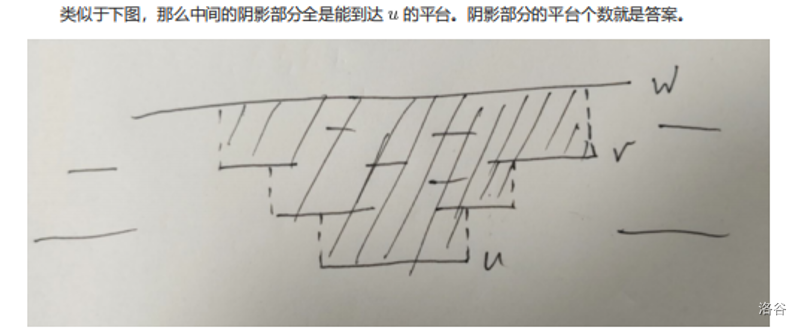
我们称连向点 \(i\) 左端点的点为 \(i\) 的左父亲,连向点 \(i\) 右端点的点为 \(i\) 的右父亲,为了方便我们在 \(n+1\) 的高度添加一条无限长的线段。
那么图中 \(w\) 这种线段就相当于,从 \(u\) 开始一直跳左父亲和右父亲,最后跳到的同一个点就是 \(w\) 了。
先考虑些琐碎的东西:
- 建图的优化,从高到低扫描线线段树做区间覆盖。
- 求左右父亲,从低到高扫描线线段树做区间覆盖。
然后考虑如何计算阴影中的线段数量,对于每条上下的边我们维护其左边有多少线段,右链左边的总数减去左链左边的总数就能算出来了,这个东西显然可以差分一下,然后扫描线树状数组维护。
至于最后的统计答案,倍增维护左右父亲和链上的左侧线段数量和,直接跳即可。
时间复杂度 \(O(n\log n)\),注意空间常数。
代码
C. polygon
题目描述
有 \(n\) 个实数 \(x_{1},x_{2},\ldots,x_{n}\),\(x_i\) 从 \((0,2^{a_i})\) 的实数中等概率随机,问不存在一个 \(x_i\) 超过 \(\sum x_i\) 的一半的概率。
\(1\le n\le 5\times 10^4\),\(0\le a_i\le 50\)。
题目分析
有一说一,这题真不难。
但是需要多重积分和 NTT,不想写了,有空回来把前一半步骤写了。
标签:子串,le,题目,log,线段,NOI2024,端点,集训,省队 From: https://www.cnblogs.com/los114514/p/18113692