P1484 种树

有 \(n\) 个坑。第 \(i\) 个坑种树的价值是 \(c_i\)，相邻坑不能同时种。可以种 \(k\) 颗树，求最大价值。

模拟费用流，建图类似这样：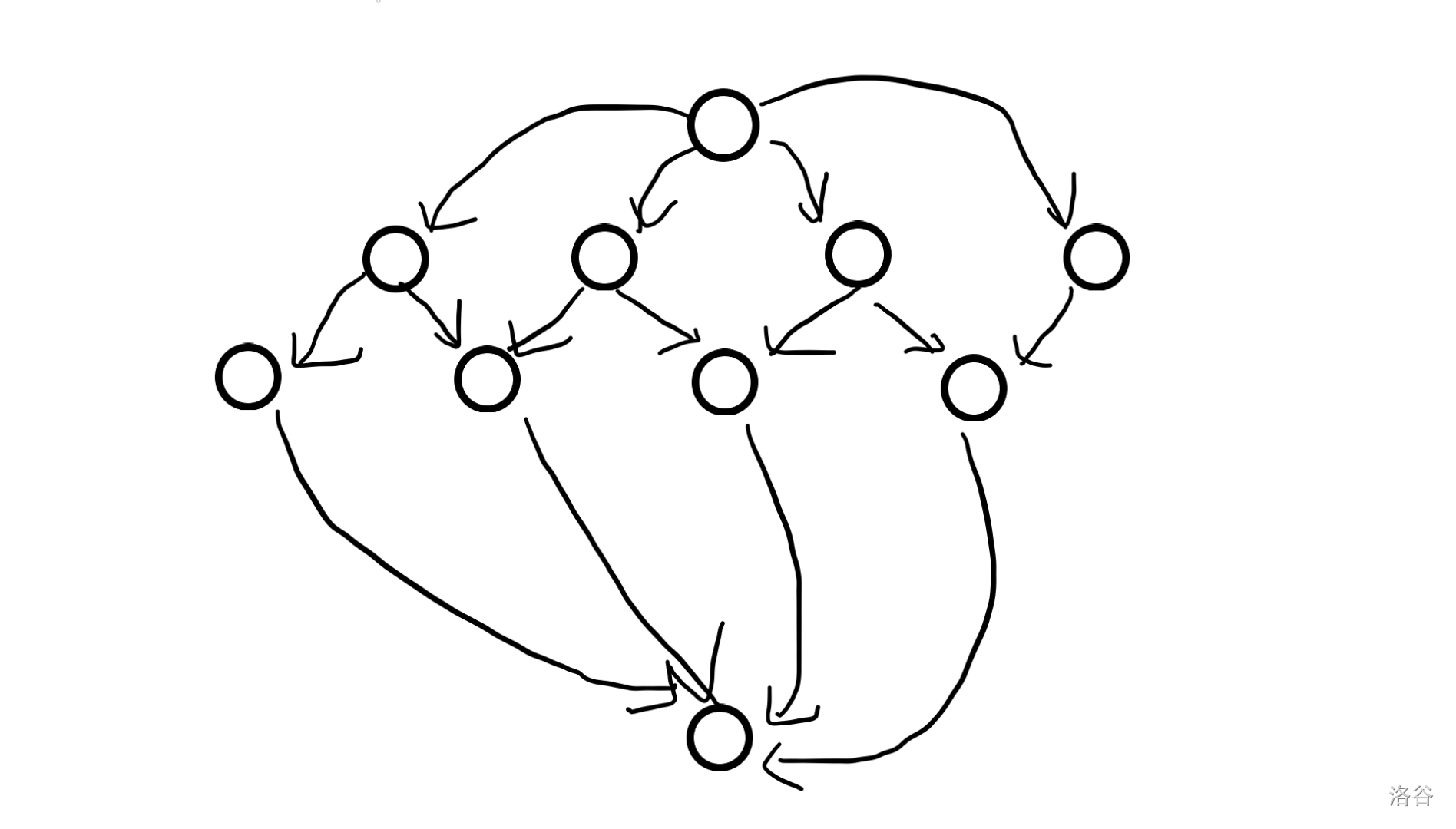

中间两层结点之间有 \(7\) 条边，表示 \(n=7\) 的情况。相邻两条边，例如 \(1,2\) 总流入量为 \(1\)，\(2,3\) 总流出量为 \(1\)，也不可能出现相邻两条边同时流的情况，对应相邻两个坑不能同时种树。

在上面的图里找增广路的时候，我们发现增广路上每条边的流量有特征：源点流出和汇点流入的边流量都是 \(0\)，其余边 \(0,1\) 不断交替且 \(0\) 开头 \(0\) 结尾：例如 0 1 0 1 0 就是一种可能的情况。

对应到原问题里，初始每个坑位都是 \(0\)。种了树就会变 \(1\)。一个区间如果开头结尾为 \(0\)、\(0,1\) 交替且区间左边一个和右边一个都是 \(0\)，这就对应一个增广路。

可见一开始每个坑位都对应一个区间，也对应一个增广路。

而更新一条增广路，会使路径上的 \(0\) 变 \(1\)，\(1\) 变 \(0\)；对应到原问题里就是区间内 \(0\) 变 \(1\)，\(1\) 变 \(0\)。

发现将区间翻转后，因为规定了一个区间左边一个右边一个为 \(0\)，且开头结尾为 \(0\)，所以反转后刚好和左右拼成一个更大的区间。

那我们可以用链表来维护这些区间。同时搞一个堆，这个堆用来每次找最大价值的区间。一个区间的价值定义为其中 \(1\) 的价值减去 \(0\) 的价值。

每次挑出一个价值最大的且未被标记为不可选的区间 \(d\)，统计其价值，同时通过链表找到它相邻的两个区间 \(d_1,d_2\)，将 \(d,d_1,d_2\) 合并为一个大区间，价值为 \(v_{d_1}+v_{d_2}-v_d\)，然后把原本的 \(d_1,d_2\) 标记为不可选。

一直挑，挑到够了 \(k\) 个就结束。