什么是人工智能
人工智能是计算机科学的一个重要分支. 也是一门正在发展中的综合性前沿学科,它是由计算机科学、控制论、信息论、神经生理学、哲学、语言学等多种学科相互渗透而发展起来的,目前正处于发展阶段尚未形成完整 休系。
人工智能三大学派——符号、连接、行为
合取析取
最简单记忆法
- 例:LIKE(I,MUSIC)∧LIKE(I,PAINTING)
- (我喜爱音乐和绘画。)
所以合取就是∧
蕴涵(Implication):“→”表示“如果—那么”(IF—THEN)关系
连词的优先级 :
¬, ∧, ∨ (\(\exists, \forall\)) , →, ↔
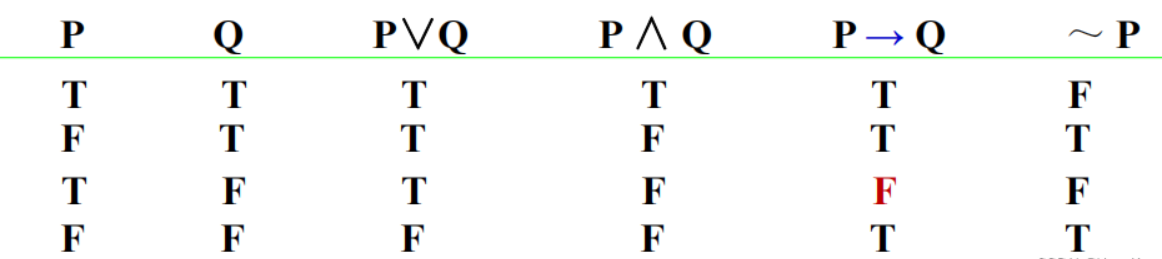
~A V B 等价于 A→B
产生式规则
什么是产生式?产生式规则的语义是什么?
产生式规则的基本形式:P->Q 或者 IF P THEN Q
P是产生式的前提(前件),用于指出该产生式是否可用的条件
Q是一组结论或操作(后件),用于指出当前提P所指示的条件满足时,应该得出的结论或应该执行的操作
产生式规则的语义:如果前提P被满足,则可推出结论Q,或执行Q所规定的操作
自然演绎推理
置换
\(\theta=\{t_{1}/x_{1},t_{2}/x_{2},\cdots,t_{n}/x_{n}\}\)
\(\lambda=\{u_{1}/y_{1},u_{2}/y_{2},\cdots,u_{m}/y_{m}\}\)是两个置换
\(\theta_{\circ}{{\lambda}}\)记作\({}^{\{}t_{1}\lambda/x_{1},\,t_{2}{\lambda}/x_{2},\,\cdots,\,t_{n}\lambda/x_{n},\,u_{1}/y_{1},\,u_{2}/y_{2},\,\cdots,\,u_{m}/y_{m}\}\)
要满足规则1:\(t_{i}{\lambda}=x_{i}\)时候,删掉\(t_{i}\lambda/x_{i}\;\;(\;i=1,\,2,\,**,\,n)\)
规则2:\(y_{j}\in\{x_{1},x_{2},\cdots,x_{n}\}\)的时候,删掉\(u_{j}/y_{j}\ (j=1,2,\ ...,m)\)
简单的例子:
\(\theta=\{f(y)/x,z/y\}\,,\,\,\,\lambda=\{a/x,\,b/y,y/z\}\)求两个的合成
\(\{f(b/y)/x,(y/z)/y,\,a/x,\,b/y,y/z\}=\{f(b)/x,y/y,\,a/x,\,b/y,y/z\}\)
然后根据规则
去掉y/y和重复的
只留下\(\theta\circ\lambda=\{f(b)/x,y/z\}\)
合一
合一就是F1,F2,F3....如果有一个\(\theta\)
符合\(F_{1}\theta=F_{2}\theta=\cdots=F_{n}\theta\)
就称\(\theta\)是F的一个合一
最一般合一:设σ是谓词公式集F的一个合一,如果对F的任意一个合一θ都存在一个置换λ,使得 θ= σ· λ,则称σ是一个最一 般(或最简单)合一
消解原理
消解 : 对谓词演算公式进行 分解、化简,消去一些符号 , 以求得导出 子
句 ,又称 归结 。
消解原理 :
(1) 一种用于 子句公式集 的重要推理规则
(2) 子句 是由文字的析取组成的公式
(3) 一个原子公式、原子公式的否定叫作 文字
注意: 不含任何文字的子句称为 空子句 。
由 子句、空子句 所构成的集合称为 子句集
消解过程 :消解规则应用于 母体子句对 , 以便产生导出子句
举例: { E1 ∨ E2 , ~ E2 ∨ E3 } 消解导出 E1 ∨ E3
两边扣掉互补的,剩下的部分析取
归结式


两边提取两个互补的子句
L1 L2 再C12=剩下的部分析取
主义 \({\cal L}_{1}=\ -\,{{Q}},{\cal L}_{2}=Q\,\)归结完得到\(C_{12}=\mathrm{NIL}\)
对于一阶谓词逻辑,若子句集是不可满足的,则必存在一个从该子句集到空子句的归结演绎整理到最后是NIL
不可满足就是指永假式 是不可满足的

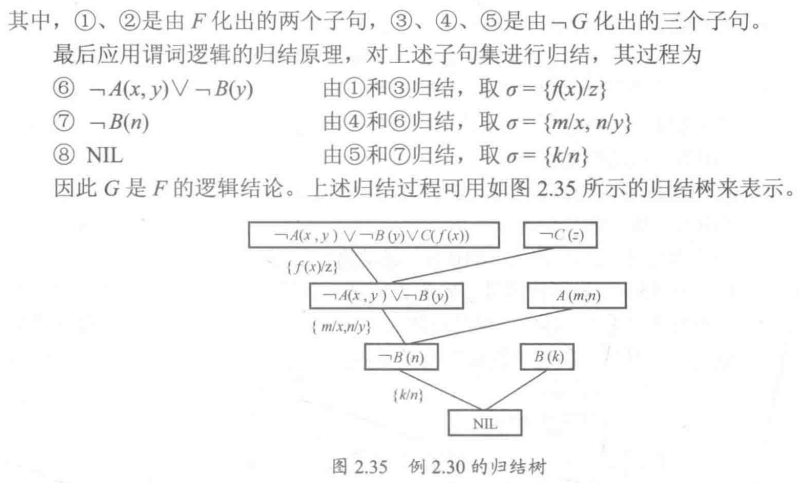
9步法求取子句集
(1)消去蕴涵符号
(2)缩小否定符号的辖域(狄·摩根定律)
(3)变量标准化(哑元唯一)
(4)消去存在量词()
(5)化为前束形
(6)化为合取范式(∧)
(7)消去全称量词()
(8)消去连词符号(∧)
(9)更换变量名(同一变量名不出现在一个以上子句)




在做题时先将F和¬G化成子句集s,如果s归结为NIL,那么就说明G是F的结论
设已知
(1)如果x是y的父亲,y是z的父亲,则x是z的祖父
(2)每一个人都有一个父亲
使用归结演绎推理证明:对于某人u,一定存在一个人v,v是u的祖父也就是下面的G
先定义谓词
F(x,y): x是y的父亲
GF(x,z): x是z的祖父
P(x):x是一个人
F1可表示为:(∀x)(∀y)(∀z)( F(x,y) ∧ F(y,z) ->GF(x,z) )
F2可表示为:(∀y)(∃x)( P(x) ->F(x,y) )
G可表示为:(∃u)(∃v)(P(u) -> GF(v,u)
将F1,F2,¬G化为子句集,S = { ¬F(x,y) v ¬F(y,z) v GF(x,z) , ¬P(a) v F(x,y),
P(u) , ¬GF(v,u) }
推理规则
IF E1 THEN (a,b) H1 P(H1)= c
P(H1 | E1) = a * c /(a-1) *c+1
P(H1|~E1)= b * c/ (b-1) * c +1
单层感知器完成逻辑与运算的学习过程
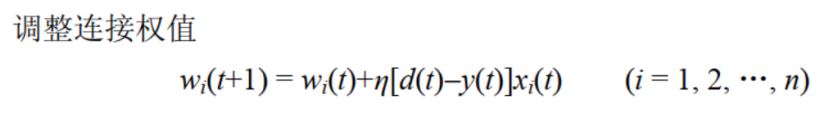
与运算的逻辑关系为:
| x1 | x2 | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
\(设w_1(0)=0.5,w_2(0)=0.7,\theta(0)=0.6,\eta=0.4\)
\(w_{1号或2号}(第几次迭代)——w的定义,\eta类似学习率\)
第一个数据为0V0=0写作\(x_1(0)=0,x_2(0)=0,期望值d(0)=0\),这里括号内的数都是迭代次数
实际值\(y(0)=f(w_1*x_1+w_2*x_2-\theta)\)
\(y(0)=f(0.5*0+0.7*0-0.6)=f(-0.6)=0\)这里的f为阶跃函数——小于0为0,大于0为1
得到的结果与期望相同,则可以继续
下一组为0V1=0—— \(x_1(0)=0,x_2(0)=1,期望0\)
\(y=f(0*0.5+1*0.7-0.4)=f(0.3)=1\)不符合期望
这个时候要更改w1和w2和theta
\(\theta(1)=\theta(0)+\eta*(期望值-实际值)*(-1)\)
\(w_1(1注意这里的1就是从0迭代到1)=w_1(0)+\eta*(期望值-实际值)*(x_1的值)\)
\(w_2(1)=w_2(0)+\eta*(期望值-实际值)*(x_1的值)\)
\(\theta(1)=原本的0.6+0.4*(0-1)*(-1)=1\)
\(w_1(1)=原本的0.5+0.4*(0-1)*(输入的0)=0.5\)
\(w_2(1)=原本的0.7+0.4*(0-1)*(输入的1)=0.3\)
这是更新完的参数
上述总结为:
设置w1,w2,theta,eta
放入x1,x2,得到y与期望d对比
没出入就继续,有出入更新设置的参数
上面验证完0V0=0,0V1=0,更新完参数直接进入下一个验证,然后下面只需重复步骤即可
当0V0,0V1,1V0,1V1全部走完或者更新之后,还要从头看0V0
当所有输入得到的输出满足期望时,才可以结束
当一步一步更新得到
\(\theta(3即更新了三次)=1\)
\(w_1(3)=0.9\)
\(w_2(3)=0.3\)时候,
对输入:“0 0”有y=f(0.90+0.30-1)=f(-1)=0
对输入:“0 1”有y=f(0.90+0.30.1-1)=f(-0.7)=0
对输入:“1 0”有y=f(0.91+0.30-1)=f(-0.1)=0
对输入:“1 1”有y=f(0.91+0.31-1)=f(0.2)=1
满足题意即可结束
hopfield网络
特点:单层全互联的对称反馈网络模型
给定v1,v2,v3,v4,\(\theta_1\),\(\theta_2\),\(\theta_3\),\(\theta_4\)
\(w_{12},w_{13},w_{14},w_{23},w_{24},w_{34}\)
公式为\(E=-\frac{1}{2}(w_{12}*v_1*v_2...就是w做排列组合加一遍)+(v_1*\theta_1....就是v和\theta组合一遍)\)
可信度推理模型CF(Certainty Factor)

给定
IF \(E_1\) THEN H (CF(H,\(E_1\)))
IF \(E_2\) THEN H (CF(H,\(E_2\)))
算出
\(CF_1(H)=CF(H,E_1)*max\{0,CF(E_1)\}\)
\(CF_2(H)=CF(H,E_1)*max\{0,CF(E_2)\}\)
然后带入公式
\(C F(H)=\)
当\(C F_{1}(H)\geq0\),\(C F_{2}(H)\geq0\)(两个都大于等于0)
\(C F_{1}(H)+C F_{2}(H)-C F_{1}(H)\times C F_{2}(H)\)
当\(C F_{1}(H)<0\),\(C F_{2}(H)<0\)(两个都小于0)
\(C F_{1}(H)+C F_{2}(H)+C F_{1}(H)\times C F_{2}(H)\)
当\(C F_{1}(H)与C F_{2}(H)异号\)
\(\frac{C F_{1}(H)+C F_{2}(H)}{1-\operatorname*{min}\{|C F_{1}(H)|,|C F_{2}(H)|\}}\)
模糊集
大多数情况下隶属度是在0---1的范围内,就接近1表示隶属度越高。
F=0.9/u1+0.7/u2+0.5/u3+0.3/u4+0/u5
G=(0/u1+0/u2+)0.6/u3+0.8/u4+1/u5
合取:∧ ——和,and,取min( ) 合取优先级>析取
析取:∨——与,or,取max( )
F∩G=(0.9∧0)/ u1+(0.7∧0)/ u2+(0.5∧0.6)/u3+(0.3∧0.8)/u4+(0∧1)/u5取两个数之小
=0/ u1+0/ u2+0.5/u3+0.3/u4+0/u5
=0.5/u3+0.3/u4
F∪G=(0.9∨0)/ u1+(0.7∨0)/ u2+(0.5∨0.6)/u3+(0.3∨0.8)/u4+(0∨1)/u5
=0.9/ u1+0.7/ u2+0. 6/u3+0.8/u4+1/u5取两个数之大
﹁F=(1-0.9)/ u1+(1-0.7)/ u2+(1-0.5)/u3+(1-0.3)/u4+(1-0)/u5
取1的补数=0.1/ u1+0.3/ u2+0.5/u3+0.7/u4+1/u5
R1与R2的合成R1οR2
\(R_{1}=\left[\begin{array}{c c c}{{0.3}}&{{0.7}}&{{0.2}}\\ {{1}}&{{0}}&{{0.4}}\\ {{0}}&{{0.5}}&{{1}}\end{array}\right]\)\(R_{2}={\left[\begin{array}{l l}{0.2}&{0.8}\\ {0.6}&{0.4}\\ {0.9}&{0.1_{}}\end{array}\right]}\)
类似与矩阵相乘(相对应的位置进行合取,不同的位置进行析取)
R(1,1)=(0.3∧0.2)∨(0.7∧0.6)∨(0.2∧0.9)= 0.2∨0.6∨0.2= 0.6
R(1,2)=(0.3∧0.8)∨(0.7∧0.4)∨(0.2∧0.1)= 0.3∨0.4∨0.1= 0.4
R(2,1)=(1∧0.2)∨(0∧0.6)∨(0.4∧0.9)= 0.2∨0∨0.4= 0.4
R(2,2)=(1∧0.8)∨(0∧0.4)∨(0.4∧0.1)= 0.8∨0∨0.1= 0.8
R(3,1)=(0∧0.2)∨(0.5∧0.6)∨(1∧0.9)= 0.2∨0.6∨0.9= 0.9
R(3,2)=(0∧0.8)∨(0.5∧0.4)∨(1∧0.1)= 0∨0.4∨0.1= 0.4
\(R_{1}\circ R_{2}={\left[\begin{array}{l l}{0.6}&{0.4}\\ {0.4}&{0.8}\\ {0.9}&{0.4}\end{array}\right]}\)
请用模糊关系Rm求出模糊结论。
模糊结论就是用另一个模糊集的隶属度与(Rm)关系进行合成操作。
模糊结论的求法:
第一步:先计算"少"与"多"这两个模糊集的Rm关系;
第二步:用较少这个模糊集与前面得到的Rm关系进行一个合成操作就可以得到模糊结论。
设U=V={1,2,3,4}
且有如下推理规则:
IF x is 少 THEN y is 多
其中,“少”与“多”分别是U与V上的模糊集,设
少=0.9/1+0.7/2+0.4/3(+0/4)
多=(0/1+)0.3/2+0.7/3+0.9/4
已知事实为
x is 较少
“较少”的模糊集为
较少=0.8/1+0.5/2+0.2/3(+0/4)
请用模糊关系Rm求出模糊结论。
设F和G分别是论域U和V上的两个模糊集
\(R_{\mathrm{m}}=\int_{u×v }\ (\mu_{F}(u)\wedge\mu_{G}(v))\vee(1-\mu_{F}(u))/(u,v)\)
"×"表示模糊集的笛卡尔乘积
先用模糊关系Rm求出规则
IF x is 少 THEN y is 多
所包含的模糊关系Rm
R(1,1)=(0.9∧0)∨(1-0.9)=0.1
R(1,2)=(0.9∧0.3)∨(1-0.9)=0.3
R(1,3)=(0.9∧0.7)∨(1-0.9)=0.7
R(1,4)=(0.9∧0.9)∨(1-0.9)=0.9
R(2,1)=(0.7∧0)∨(1-0.7)=0.3
R(2,2)=(0.7∧0.3)∨(1-0.7)=0.3
R(2,3)=(0.7∧0.7)∨(1-0.7)=0.7
R(2,4)=(0.7∧0.9)∨(1-0.7)=0.7
R(3,1)=(0.4∧0)∨(1-0.4)=0.6
R(3,2)=(0.4∧0.3)∨(1-0.4)=0.6
R(3,3)=(0.4∧0.7)∨(1-0.4)=0.6
R(3,4)=(0.4∧0.9)∨(1-0.4)=0.6
R(4,1)=(0∧0)∨(1-0)=1
R(4,2)=(0∧0.3)∨(1-0)=1
R(4,3)=(0∧0.7)∨(1-0)=1
R(4,4)=(0∧0.9)∨(1-0)=1
得到\(R_m\)
计算Y'=\(\{0.8,0.5,0.2,0\}{\circ}\)\(\left[\begin{array}{l l l l}{{0.1}}&{{0.3}}&{{0.7}}&{{0.9}}\\ {{0.3}}&{{0.3}}&{{0.7}}&{{0.7}}\\ {{0.6}}&{{0.6}}&{{0.6}}&{{0.6}}\\ {{1}}&{{1}}&{{1}}&{{1}}\end{array}\right]\)
=\(\{0.3,0.3.0.7,0.8\}\)
贝叶斯网络
联合概率公式:\(P(x_{1},x_{2},\cdots,x_{n})=\prod_{i=1}^{n}P(X_{i}\mid\mathrm{par}(X_{i}))\)
其实就是\(\mathsf{P(x1,x2,x3,x4)=p(x1)^{*}p(x2|x1)^{*}p(x3|x1,x2)^{*}p(x4|x1,x2,x3)}\)
机试记忆点
每个数字保留5个位宽:printf("%5d",i);
多组输入用
whlie(cin>>n)
{
}
或者
while(scanf("%d",&n)!=EOF)
{
}
质数筛问题,复杂度为O(n)级别的
for(int i=2;i<maxn;i++)//对2到maxn所有的数,打表判断是否为素数
{
if(!isComposite[i])//如果这个数字已经标记为素数
prime.push_back(i);//放入素数数组
for(int j=0;j<prime.size();j++)
{
if(i*prime[j]>Maxn)//超出打表范围,不能标记
break;
isComposite[i*prime[j]]=1;//当前i和数组中的数相乘,对这些数标记为合数
if(i%prime[j]==0)//继续的话重复标记,所以break
break;
}
}
加入maxn为1e5
则prime数组里的就是小于1e5的所有素数
1不是素数!!!!!
质数是在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。因此,1的因数只有1和它本身,不符合质数的定义
函数来比较绝对值大小
bool abs_cmp(const int &x,const int &y)
{
return abs(x) > abs(y);
}
去重+排序用stl容器set
#include<set>
set<int> s;
s.insert(x);//插入的时候有重复的就不会插入
//默认从小到大排序
遍历直接用
for(auto n : s)
cout<<n;
set<int> s1; // 默认从小到大排序
set<int, greater<int> > s2; // 从大到小排序
//逆序对问题专解——用归并排序
void Merge(int left,int middle,int right){
int i = left;
int j = middle + 1;
int k = left;
while(i <= middle && j <= right){
if(arr[i] <= arr[j]){
temp[k++] = arr[i++];
}else{
number += middle + 1 - i; //前半段是有序,都可以与后面这个数构成逆序对
temp[k++] = arr[j++];
}
}
while(i<=middle) temp[k++] = arr[i++];
while(j <= right) temp[k++] = arr[j++];
for(k = left;k <= right; k++){
arr[k] = temp[k];
}
}
//归并排序求解逆序对数
void mergeSort(int left, int right){
if(left < right){
int middle = left + (right - left)/2;
mergeSort(left, middle);
mergeSort(middle + 1, right);
Merge(left,middle,right);
}
}
//dijkstra算法标准模板
#include <iostream>
#include <algorithm>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int maxn = 100005;
struct Edge{
int to;
int weight;
bool operator<(const Edge &other) const
{
return other.weight <weight;
}
};
int dist[maxn];
vector<Edge> adj_list[maxn];
bool visit[maxn];
void dijkstra(int start)
{
memset(dist,0x3f,sizeof(dist));
priority_queue<Edge> queue;
dist[start]=0;
queue.push(Edge{start,0});
while(!queue.empty())
{
Edge edge = queue.top();
queue.pop();
int u=edge.to;
if(visit[u]) continue;
visit[u] = true;
for(Edge &e:adj_list[u])
{
int v = e.to;
int u_to_v_weight = e.weight;
if(dist[v] >= dist[u] + u_to_v_weight)
{
dist[v] = dist[u] +u_to_v_weight;
queue.push(Edge{v,dist[v]});
}
}
}
}
int main()
{
int n,m,s;
cin>>n>>m>>s;
for(int i=0;i<m;i++)
{
int u,v,w;
cin>>u>>v>>w;
adj_list[u].push_back(Edge{v,w});
}
dijkstra(s);
for(int i=1;i<=n;i++)
cout<<dist[i]<<" ";
}
//并查集
int getroot(int a) //并查集 ,并返回a的根节点
{
while(arr[a]!=a)
{
a=arr[a];
}
return a;
}
if(z==2) //判断是否是同一个根下
{
if(getroot(x) == getroot(y)) cout<<'Y'<<endl;
else cout<<"N"<<endl;
}else //z==1
{
int p_x=getroot(x);
int p_y=getroot(y);
if(p_x>p_y) arr[p_x] = p_y; //连接两个根
else arr[p_y]=p_x;
}
//prim模板
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MaxInt=1e9+7;
const ll MaxLL=1e18+7;
const int Maxn =2e3+7;
int n,m;
bool vis[Maxn]; //标记数组
int arr[Maxn][Maxn];
ll lowc[Maxn]; //每个点加入最小生成树的代价
void Init()
{
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
arr[i][j]=arr[j][i]=MaxInt;
}
}
ll Prim()
{
vis[1]=1;//假设选定1号点加入最小生成树
ll ans=0;
for(int i=2;i<=n;i++)
lowc[i]=arr[i][1];
for(int i=1;i<n;i++)
{
ll Min=MaxLL;//找最小代价先初始化大的值
int node=-1;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&lowc[j]<Min)
{
Min=lowc[j];
node=j;
}
}
ans+=Min;//答案加上最小代价
vis[node]=1;
for(int j=1;j<=n;j++)
{
if(!vis[j] && lowc[j]>arr[node][j])
lowc[j]=arr[node][j];
}
}
return ans;
}
int main() {
cin>>n>>m;
Init();
int x,y,value;
for(int i=0;i<m;i++)
{
cin>>x>>y>>value;
arr[x][y] = arr[y][x]=min(arr[x][y],value);
}
ll ans=Prim();
cout<<ans<<endl;
return 0;
}
//dfs解决全排列问题——用vis数组
bool vis[maxn];
int ans[maxn];
void arrange(int t,int n)
{
if(t>n)
{
for(int i=1;i<=n;i++)
{
cout<<ans[i];
}
cout<<endl;
}
else
{
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
ans[t]=i;
vis[i]=true;
arrange(t+1,n);
vis[i]=false;
}
}
}
}
int main()
{
int n;
cin>>n;
arrange(1,n);
return 0;
}
//回溯法解决全排列
int list[maxn];
void Perm(int list[],int i,int n)
{
if(i==n)
{
for(int i=1;i<=n;i++)
cout<<list[i];
cout<<endl;
}
for(int t=i;t<=n;t++)
{
swap(list[t],list[i]);
Perm(list,i+1,n);
swap(list[t],list[i]);
}
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>list[i];
Perm(list,1,n);
return 0;
}
//经典n皇后问题
#include<iostream>
#include<algorithm>
using namespace std;
int column[13];
bool col_visit[13];
bool row_visit[13];
bool diag1_visit[30];
bool diag2_visit[30];
int ans = 0;
void dfs(int n,int i)
{
if(i == n)
{
if(ans < 3)
{
for(int j=0;j<n;j++)
{
cout<<column[j]<<" ";
}
cout<<endl;
}
ans++;
return;
}
for(int j=0;j<n;j++)
{
if(row_visit[i] || col_visit[j] || diag1_visit[i+j] || diag2_visit[j-i+13])
continue;
row_visit[i] = true;
col_visit[j] = true;
diag1_visit[i+j] = true;
diag2_visit[j-i+13] = true;
column[i] = j+1;
dfs(n,i+1);
row_visit[i] = false;
col_visit[j] = false;
diag1_visit[i+j] = false;
diag2_visit[j-i+13] = false;
}
}
int main()
{
int n;
cin>>n;
dfs(n,0);
cout<<ans<<endl;
return 0;
}
vector数组初始化
vector<int> dp(n,0);
表示为长度为n,所有值为0
或者vector<int> vect{ 10, 20, 30 };
//最大字段和问题新解法
//遇到负数的就变掉current
//遇到正数就在current的基础上+这个数
//期间不断维护ans值
int main()
{
int n;
cin>>n;
int ans = INT_MIN;
int current = INT_MIN;
for(int i=0;i<n;i++)
{
int temp;
cin>>temp;
if(current<0)
current = temp;
else
current+=temp;
ans = max(ans,current);
}
cout<<ans<<endl;
return 0;
}
动态规划爬楼梯问题
dp[i] = dp[i-1] + dp[i-2]
你要爬到第10层楼梯,只需要把爬到第8层的方法和爬到第9层的方法加起来就行了
不过注意dp[1]=1、dp[2]=1
贪心问题中找零钱张数最小问题
无敌找钱策略
其中coins[]必须从大到小找钱。
int calculate(int num)
{
int sum=0;
for(int i=0;i<6;i++)
{
sum+=num/coins[i];
num=num%coins[i];
}
return sum;
}