扫描线

是什么 & 矩形面积并

本质上可以理解为，对一个二维（或多维）平面上的问题，通过扫描一维，并且用数据结构动态维护另一位的增减性。

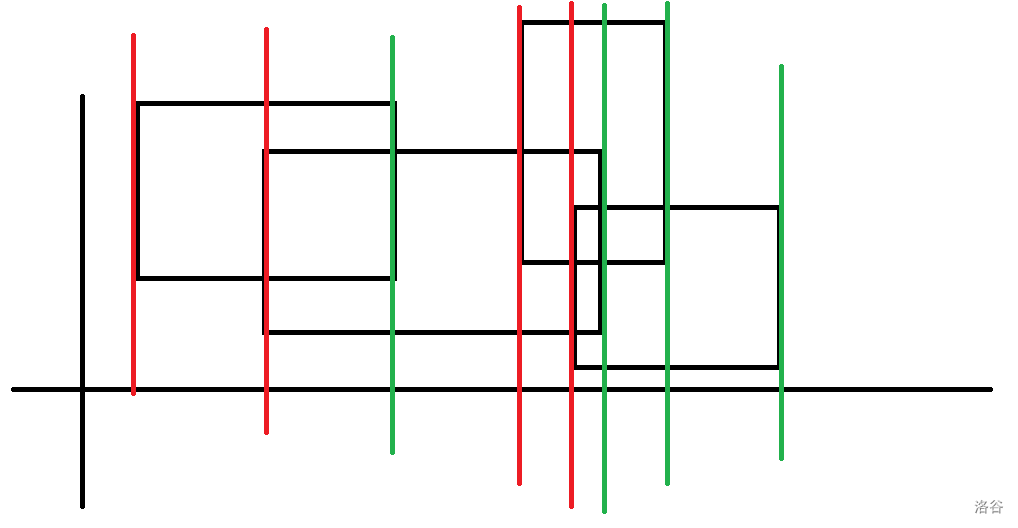
我们对于 \(x\) 轴扫描，那么会对面积构成影响的 \(y\) 显然只有红色的几条和绿色的几条。

容易发现，这样的线的数量是 \(2n\) 的（\(n\) 为矩形个数）。

所以可以理解为如下的问题：

有 \(2n\) 次操作，维护一个数组，有如下两种操作。

• 对一个区间 \([l,r]\) 加上 \(\Delta\)。
• 求 \(\sum [a_i>0]\)。

满足 \(n\le 10^5,\Delta \in \{1,-1\},l\le r\le 10^9\)。

这个问题看起来就很可以用数据结构维护，但是我们需要先把 \([l,r]\) 做离散化（实际上 \(a_i\) 极长连续段个数是 \(\mathcal O(n)\) 的），维护这些段的左右端点即可。

然后我们令一个节点的 \(len\) 表示这个节点的管辖范围内，\([a_i>0]\) 的个数。显然有 \(len_u=len_{lson_u}+len_{rson_u}\)。最后答案是 \(len_1\)。

所以我们只需要考虑前一个问题如何维护即可。再维护一个数 \(cover\)，表示 \(u\) 所管辖的范围内，被完整覆盖了几次。

如果被完整覆盖了，那么 \(len_u\) 必然是 \(u\) 管辖的左右端点离散化以前的数。否则，\(len_u=len_{lson_u}+len_{rson_u}\) 即可。这样就形成了完整的 pushup 和 pushdown ，构建好了线段树。

矩形周长并

首先，我们发现垂直于 \(x\) 轴和平行于 \(x\) 轴的边是类似的，所以我们分别处理即可。因此，下文只考虑平行于 \(x\) 轴的边。

还是像上文那样切成若干条线。一条线 \(ln\) 对于周长的贡献是 \(|(原周长 \cup ln)-原周长|\)​。所以我们像上文那样维护目前覆盖的长度即可，把两个方向的线段的答案加起来即可，和面积并的代码差别极小。

其他例题

[NOI2023] 方格染色

先考虑不同寻常的操作三。这玩意只会有 \(5\) 次，显然每次操作对 \(\mathcal O(n)\) 个格子有影响，然后 \(n,q\) 在前 \(95\) 分同阶，所以稍加转换就变成了典中典矩形面积并，时间复杂度 \(\mathcal O ((n+q)\log q)\)，期望得分 \(95\) 分。

然后，我们考虑最后 \(5\) 分怎么做：

我们考虑一个斜率为 \(1\) 的一次函数，它与任何一条在这个平面直角坐标系内的直线都至多有一格相交。我们先把所有前两种操作带来的线处理后，再将斜线与每一条直线相交的位置用 map 记录下，考虑这样的交点有几个，用总覆盖面积减去这样的交点个数即可，代码不好写。时间复杂度 \(O(q\log q)\)。

P1908 逆序对

这玩意显然你用树状数组/归并排序啥的都可以做。

那么我们来考虑怎么转化成扫描线模型。

考虑将 \((a_i,i)\) 放在一个平面直角坐标系中，则对于每一个点，我们计算 \([(1,n),(a_i,i)]\) 内点的个数即可。

P1972 [SDOI2009] HH的项链

显然，这是一道莫队典题，可以在 \(O(n\sqrt m)\) 的时间复杂度内做完这道题，期望得到 \(60\) 分，显然你实现的精细一点的话也是可以过的。

不考虑莫队做法，将这道题转化到平面直角坐标系上，问题可以转化成 将 \((i,a[i])\) 放在一个平面直角坐标系中，对于 \([l,r]\) 的答案极为，在 \([(l_0,0),(r_0,A)]\)​ 中点的不同纵坐标有几个。这玩意你用树状数组稍微维护一下就可以了，甚至不需要线段树。

总结

总而言之，扫描线的思路就是数据结构维护一维，暴力模拟另一维。所有数组和下标都对答案有影响的题目，都可以把数组的每一项转化成 \((\text{值},\text{下标})\)。