学了分块,感觉这玩意好难啊,怎么听起来这么简单?【】【】分块!
先推荐一个东西:loj 分块全家桶!
首先,把一整个数组劈成 \(\sqrt n\) 块是最优的!(当然如果你想写一个 \(114514\) 块的分块也没问题但他不优啊!)
长这样:
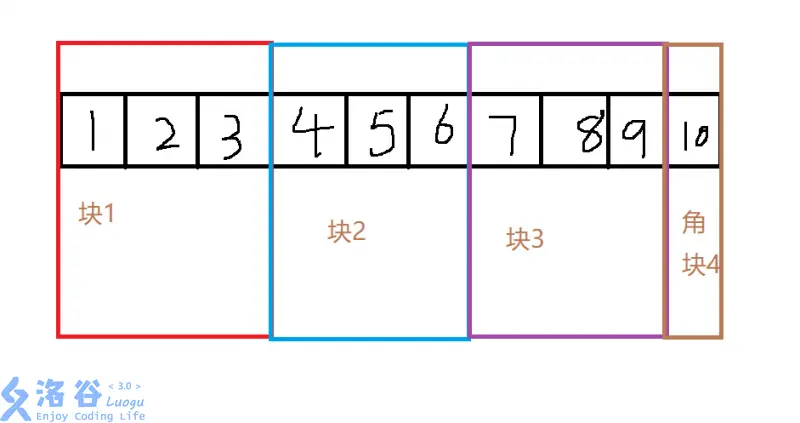
这样它的复杂度是:
- 预处理:\(O(n\sqrt n+q)\)
- 在线处理:\(O(q\sqrt n+n)\)
分块其实就是三层的树,每个非叶子结点的节点有 \(\sqrt n\) 个子节点。
像这样:
(第一层:整个大区间,第二层:每个块,第三层:每个位置)
然后呢?
没了。
你问咋处理?每个块的处理,两边的“散块”就暴力啊!
分块的思路很简单。
但某些毒瘤题的代码不做评价。
T1
模板。只放代码注释不放解析。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 __int128
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,a[50010],lz[50010],op,l,r,c,kc;
//kc:块长(根号n),lz:类似lazytag,给整个块的标记
LL q(LL x)
{
return lz[x/kc]+a[x];
}
void ud(LL l,LL r,LL c)
{
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
a[i]+=c;
}
}
else
{
rep(i,l,(l/kc+1)*kc-1,1)a[i]+=c;
rep(i,r/kc*kc,r,1)a[i]+=c;
//两边的散块
repn(i,l/kc+1,r/kc,1)lz[i]+=c;
//中间的整块
}
}
int main()
{
cin>>n;
kc=sqrt(n);
rep(i,1,n,1)cin>>a[i];
rep(i,1,n,1)
{
cin>>op>>l>>r>>c;
if(!op)
{
ud(l,r,c);
}
else
{
cout<<q(r)<<endl;
}
}
return 0;
}
T2
这道题目的基础是咋求一个数 \(c\) 在 \(\left [l,r\right ]\) 的排名。
咋办?肯定二分啊!排个序!
void px(LL x)
{
rep(i,max(1LL,x*kc),min(n,kc*(x+1)-1),1)b[i]=a[i];
sort(b+max(1LL,x*kc),b+min(n+1,(x+1)*kc));
}
为什么排序用
b[i]而不是用a[i]?
两边的散块:你这么说,我不存在?
你排序,和原来不一样了,散块表示:你【】【】!
剩下的有手就行。
有个坑点,记得及时排序。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,a[50010],b[50010],lz[50010],op,l,r,c,kc;
LL q(LL l,LL r,LL c)
{
LL sum=0;
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
if(a[i]+lz[i/kc]<c)sum++;
}
}
else
{
rep(i,l,min(n,(l/kc+1)*kc-1),1)
{
if(a[i]+lz[i/kc]<c)sum++;
}
rep(i,r/kc*kc,r,1)
{
if(a[i]+lz[i/kc]<c)sum++;
}
repn(i,l/kc+1,r/kc,1)
{
LL l=i*kc-1,r=(i+1)*kc,mid;
while(l+1<r)
{
mid=l+r>>1;
if(b[mid]+lz[i]<c)l=mid;
else r=mid;
}
sum+=l-i*kc+1;
}
}
return sum;
}
void px(LL x)
{
rep(i,max(1LL,x*kc),min(n,kc*(x+1)-1),1)b[i]=a[i];
sort(b+max(1LL,x*kc),b+min(n+1,(x+1)*kc));
}
void ud(LL l,LL r,LL c)
{
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
a[i]+=c;
}
px(l/kc);
}
else
{
rep(i,l,min(n,(l/kc+1)*kc-1),1)a[i]+=c;
rep(i,r/kc*kc,r,1)a[i]+=c;
px(l/kc);
px(r/kc);
repn(i,l/kc+1,r/kc,1)lz[i]+=c;
}
}
int main()
{
cin>>n;
kc=sqrt(n);
rep(i,1,n,1)
{
read(a[i]);
}
rep(i,0,n/kc,1)
{
px(i);
}
rep(i,1,n,1)
{
read(op);
read(l);
read(r);
read(c);
if(!op)
{
ud(l,r,c);
}
else
{
write(q(l,r,c*c));
puts("");
}
}
return 0;
}
T3
和上一题几乎一样。
就是维护排好序的序列。
对了我上题写的太石山了就重新写了一遍&改了自己的模板。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 100010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void writing(i128 x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(i128 x)
{
if(x<0)
{
cout<<'-';
x=-x;
}
writing(x);
}
LL n,a[N],b[N],add[N],st[N],ed[N],pos[N],op,l,r,c,x,num;
vector<LL>sum[N];
void build()
{
x=sqrt(n);
num=n/x;
if(n%x)num++;
rep(i,1,num,1)
{
st[i]=(i-1)*x+1;
ed[i]=x*i;
}
ed[num]=n;
rep(i,1,n,1)
{
pos[i]=(i-1)/x+1;
sum[pos[i]].push_back(a[i]);
}
rep(i,1,num,1)sort(sum[i].begin(),sum[i].end());
}
void change(LL l,LL r,LL k)
{
LL p=pos[l],q=pos[r];
if(p==q)
{
rep(i,l,r,1)
{
a[i]+=k;
}
sum[p].clear();
rep(i,st[p],ed[p],1)
{
sum[p].push_back(a[i]);
}
sort(sum[p].begin(),sum[p].end());
return;
}
repn(i,p+1,q,1)
{
add[i]+=k;
}
rep(i,l,ed[p],1)
{
a[i]+=k;
}
sum[p].clear();
rep(i,st[p],ed[p],1)
{
sum[p].push_back(a[i]);
}
sort(sum[p].begin(),sum[p].end());
rep(i,st[q],r,1)
{
a[i]+=k;
}
sum[q].clear();
rep(i,st[q],ed[q],1)
{
sum[q].push_back(a[i]);
}
sort(sum[q].begin(),sum[q].end());
}
LL ask(LL l,LL r,LL k)
{
LL ans=-1,p=pos[l],q=pos[r];
if(p==q)
{
rep(i,l,r,1)if(a[i]+add[p]<k)ans=max(ans,a[i]+add[p]);
return ans;
}
repn(i,p+1,q,1)
{
LL tt=lower_bound(sum[i].begin(),sum[i].end(),k-add[i])-sum[i].begin();
if(tt==0)continue;
ans=max(ans,add[i]+sum[i][tt-1]);
}
rep(i,l,ed[p],1)if(a[i]+add[p]<k)ans=max(ans,a[i]+add[p]);
rep(i,st[q],r,1)if(a[i]+add[q]<k)ans=max(ans,a[i]+add[q]);
return ans;
}
int main()
{
cin>>n;
rep(i,1,n,1)
{
read(a[i]);
}
build();
rep(i,1,n,1)
{
read(op);
read(l);
read(r);
read(c);
if(!op)
{
change(l,r,c);
}
else
{
write(ask(l,r,c));
puts("");
}
}
return 0;
}
T4
水题,维护一段块的和。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,a[50010],lz[50010],ss[50010],op,l,r,c,kc;
LL q(LL l,LL r,LL c)
{
LL sum=0;
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
sum+=a[i]%c+lz[i/kc]%c;
sum%=c;
}
}
else
{
rep(i,l,(l/kc+1)*kc-1,1)
{
sum+=a[i]%c+lz[i/kc]%c;
sum%=c;
}
rep(i,r/kc*kc,r,1)
{
sum+=a[i]%c+lz[i/kc]%c;
sum%=c;
}
repn(i,l/kc+1,r/kc,1)
{
sum+=ss[i];
sum%=c;
}
}
return sum;
}
void ud(LL l,LL r,LL c)
{
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
a[i]+=c;
ss[i/kc]+=c;
}
}
else
{
rep(i,l,(l/kc+1)*kc-1,1)
{
a[i]+=c;
ss[i/kc]+=c;
}
rep(i,r/kc*kc,r,1)
{
a[i]+=c;
ss[i/kc]+=c;
}
repn(i,l/kc+1,r/kc,1)
{
lz[i]+=c;
ss[i]+=c*kc;
}
}
}
int main()
{
cin>>n;
kc=sqrt(n);
rep(i,1,n,1)read(a[i]);
rep(i,1,n,1)ss[i/kc]+=a[i];
rep(i,1,n,1)
{
read(op);
read(l);
read(r);
read(c);
if(!op)
{
ud(l,r,c);
}
else
{
write(q(l,r,c+1));
puts("");
}
}
return 0;
}
T5
啊?根号可以用分块吗?——刚开题的时候的我beeeeeeeeeee like
直到我想起一道题,但是忘了是哪道。
你想啊,就这么点数据范围(也许 \(a_i\) 范围上到 LONG_LONG_MAX 都可以做!),根号不是几下就废了吗?(变成 \(1\) 或者 \(0\))
没算是几下,应该是不超过 \(10\) 下,够了。
所有部分,包括两头散块和中间整块,都可以用一个 sol 函数解决。
这个函数干嘛呢?
把需要处理的块内部还可以开方的开方。
好了就是这么简单。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void writing(i128 x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(i128 x)
{
if(x<0)
{
cout<<'-';
x=-x;
}
writing(x);
}
LL n,a[50010],ss[50010],op,l,r,c,kc;
vector<LL>b[50010];
LL q(LL l,LL r)
{
LL sum=0;
if(l/kc==r/kc)
{
rep(i,l,r,1)
{
sum+=a[i];
}
}
else
{
rep(i,l,(l/kc+1)*kc-1,1)
{
sum+=a[i];
}
rep(i,r/kc*kc,r,1)
{
sum+=a[i];
}
repn(i,l/kc+1,r/kc,1)
{
sum+=ss[i];
}
}
return sum;
}
void sol(LL l,LL r)
{
LL po=l/kc;
repn(i,0,b[po].size(),1)
{
LL j=b[po][i];
if(j>=l&&j<=r)
{
ss[po]-=a[j];
a[j]=sqrt(a[j]);
ss[po]+=a[j];
if(a[j]<=1)
{
b[po].erase(b[po].begin()+i--);
}
}
}
}
void ud(LL l,LL r)
{
if(l/kc==r/kc)
{
sol(l,r);
}
else
{
sol(l,(l/kc+1)*kc-1);
sol(r/kc*kc,r);
repn(i,l/kc+1,r/kc,1)
{
sol(i*kc,(i+1)*kc-1);
}
}
}
int main()
{
cin>>n;
kc=sqrt(n);
rep(i,1,n,1)read(a[i]);
rep(i,1,n,1)
{
b[i/kc].push_back(i);
ss[i/kc]+=a[i];
}
rep(i,1,n,1)
{
read(op);
read(l);
read(r);
read(c);
if(!op)
{
ud(l,r);
}
else
{
write(q(l,r));
puts("");
}
}
return 0;
}
T6
我【】【】【】【】【】【】【】【】【】【】【】【】【】【】【】分块跑链表玩你【】【】【】【】【】【】——刚开题的我beeeeeeeeeeee like
结果口胡了个算法后来发现是正解?
是这样的,如果我们每个块内用其它数据结构,是能够支持其它不一样的操作的,比如这题是 vector,每次插入时先找到位置所在的块,再暴力插入,把块内的其它元素直接向后移动一位。
当然你想用链表也是可以的。
等会,万一复杂度炸了咋办?比如某个块你疯狂往里面插入。
那就重构我们的分块啊!
每 \(\sqrt n\) 次插入后,重新把数列分一下块(像最开始那样),重构需要的复杂度为 \(O(n)\),重构的次数最多 \(\sqrt n\),所以复杂度没有问题。
结果,脑子:哇真的可以!手:怎么玩?!
好吧,菜就多练(对自己说)。
对了我换了个机子结果把原来的模板忘了所以叕重构了代码。
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 200010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL int
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
i128 read()
{
i128 f=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
return x;
}
void writing(i128 x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(i128 x)
{
if(x<0)
{
cout<<'-';
x=-x;
}
writing(x);
}
LL n,m,bl,a[100005],s[200005],tp;
vector<LL>v[1005];
pll q(LL b)
{
LL x=1;
while(b>v[x].size())
{
b-=v[x].size();
x++;
}
return mkp(x,b-1);
}
void reb()
{
tp=0;
rep(i,1,m,1)
{
for(vector<LL>::iterator j=v[i].begin();j!=v[i].end();j++)s[++tp]=*j;
v[i].clear();
}
LL blo=sqrt(tp);
rep(i,1,tp,1)v[(i-1)/blo+1].push_back(s[i]);
m=(tp-1)/blo+1;
}
void ins(LL a,LL b)
{
pll t=q(a);
v[t.first].insert(v[t.first].begin()+t.second,b);
if(v[t.first].size()>20*bl)reb();
}
int main()
{
cin>>n;
bl=sqrt(n);
rep(i,1,n,1)cin>>a[i];
rep(i,1,n,1)v[(i-1)/bl+1].push_back(a[i]);
m=(n-1)/bl+1;//最开始这里写成(n-1)*bl+1了,直接爆炸!
rep(i,1,n,1)
{
LL op,a,b,c;
cin>>op>>a>>b>>c;
if(!op)ins(a,b);
else
{
pll t=q(b);
cout<<v[t.first][t.second]<<endl;
}
}
return 0;
}
T9
教练讲了这题所以我先做T9诶嘿
这题可以用莫队,但是他的双倍经验P4168不行。
这里我的思路是P4168一篇题解的,感谢其作者。
解析我觉得他说的很好了我就不打了(
本题代码
#include<stdio.h>
#include<bits/stdc++.h>
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
i128 read()
{
i128 f=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
return x;
}
void writing(i128 x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(i128 x)
{
if(x<0)
{
cout<<'-';
x=-x;
}
writing(x);
}
const LL N=100010,M=100010,K=1010;
LL n,m,tot,len,l,r,ans;
LL a[N],b[N],p[N],s[K][N],L[K],R[K],pp[K][K],bok[N];
LL cnt;
void lsh()
{
len=sqrt(n);
memset(L,0x3f,sizeof(L));
rep(i,1,n,1)
{
p[i]=(i-1)/len+1;
L[p[i]]=min(L[p[i]],i);
R[p[i]]=max(R[p[i]],i);
a[i]=read();
b[i]=a[i];
}
sort(b+1,b+1+n);
tot=unique(b+1,b+1+n)-b-1;
rep(i,1,n,1)a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
}
void ycl()
{
rep(i,1,n,1)rep(j,p[i],p[n],1)s[j][a[i]]++;
rep(i,1,p[n],1)
{
memset(bok,0,sizeof(bok));
rep(j,i,p[n],1)
{
pp[i][j]=pp[i][j-1];
rep(k,L[j],R[j],1)
{
bok[a[k]]++;
if((bok[a[k]]>bok[pp[i][j]])||(bok[a[k]]==bok[pp[i][j]]&&a[k]<pp[i][j]))pp[i][j]=a[k];
}
}
}
memset(bok,0,sizeof(bok));
}
LL q(LL l,LL r)
{
if(p[r]-p[l]<=2)
{
LL res=0;
rep(i,l,r,1)
{
bok[a[i]]++;
if(bok[a[i]]>bok[res]||(bok[a[i]]==bok[res]&&a[i]<res))res=a[i];
}
rep(i,l,r,1)bok[a[i]]=0;
return res;
}
LL res=0;
rep(i,l,R[p[l]],1)if(!bok[a[i]])bok[a[i]]+=s[p[r]-1][a[i]]-s[p[l]][a[i]];
rep(i,L[p[r]],r,1)if(!bok[a[i]])bok[a[i]]+=s[p[r]-1][a[i]]-s[p[l]][a[i]];
rep(i,l,R[p[l]],1)
{
bok[a[i]]++;
if(bok[a[i]]>bok[res]||(bok[a[i]]==bok[res]&&a[i]<res))res=a[i];
}
rep(i,L[p[r]],r,1)
{
bok[a[i]]++;
if(bok[a[i]]>bok[res]||(bok[a[i]]==bok[res]&&a[i]<res))res=a[i];
}
LL k=pp[p[l]+1][p[r]-1];
LL lxl=s[p[r]-1][k]-s[p[l]][k];
rep(i,l,R[p[l]],1)lxl+=(a[i]==k);
rep(i,L[p[r]],r,1)lxl+=(a[i]==k);
if(lxl>bok[res]||(lxl==bok[res]&&k<res))res=k;
rep(i,l,R[p[l]],1)bok[a[i]]=0;
rep(i,L[p[r]],r,1)bok[a[i]]=0;
return res;
}
int main()
{
cin>>n;
lsh();
ycl();
m=n;
rep(i,1,m,1)
{
l=read();
r=read();
if(l>r)swap(l,r);
cout<<(ans=b[q(l,r)])<<endl;
}
return 0;
}
T7
感谢@Lixiang_is_potato和她的大号@MinimumSpanningTree(请勿在没有事的情况下向其大号发送任何私信或@)提供的思路,我要给她发——奖——状!
想不到 yeeeeeeee 点怎么做
她改完错以后还把原贴删了,我好感动啊
帮她改了错后突然发现这玩意好简单...
I have a problem(可以借鉴这题 tag 的思路),
I have a 分块!
A————————C!
好了不闹了正经的。
搞俩 tag:T1 那种加的,和乘的。
处理乘修改的时候,乘标记要乘,记得把加的也乘了。
加法只有加标记要加。
然后对于散块,我们可以不管直接暴力更新!
同学的代码,简洁、明了
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=100100,M=1100;
const ll MOD=10007;
int n,op,x,y,block,nk,st[M],ed[M],p[N];
ll a[N],sum[M],add[M],c;
void build()
{
block=sqrt(n);
nk=n/block;
if(n%block!=0) nk++;
for(int i=1;i<=nk;i++) st[i]=(i-1)*block+1,ed[i]=st[i]+block-1,sum[i]=1;
ed[nk]=n;
for(int i=1;i<=n;i++) p[i]=(i-1)/block+1;
}
void hy(int k)
{
for(int i=st[k];i<=ed[k];i++) a[i]=(a[i]*sum[k]+add[k])%MOD;
sum[k]=1,add[k]=0;
}
void update_j(int l,int r,ll num)
{
int kl=p[l],kr=p[r];
if(kl==kr)
{
hy(kl);
for(int i=l;i<=r;i++) a[i]+=num,a[i]%=MOD;
}
else
{
for(int i=kl+1;i<=kr-1;i++) add[i]+=num,add[i]%=MOD;
hy(kl);
for(int i=l;i<=ed[kl];i++) a[i]+=num,a[i]%=MOD;
hy(kr);
for(int i=st[kr];i<=r;i++) a[i]+=num,a[i]%=MOD;
}
}
void update_c(int l,int r,ll num)
{
int kl=p[l],kr=p[r];
if(kl==kr)
{
hy(kl);
for(int i=l;i<=r;i++) a[i]*=num,a[i]%=MOD;
}
else
{
for(int i=kl+1;i<=kr-1;i++) sum[i]*=num,sum[i]%=MOD,add[i]*=num,add[i]%=MOD;
hy(kl);
for(int i=l;i<=ed[kl];i++) a[i]*=num,a[i]%=MOD;
hy(kr);
for(int i=st[kr];i<=r;i++) a[i]*=num,a[i]%=MOD;
}
}
ll query(int l)
{
int k=p[l];
ll ans=(a[l]*sum[k]+add[k])%MOD;
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),a[i]%=MOD;
build();
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%lld",&op,&x,&y,&c);
c%=MOD;
if(!op) update_j(x,y,c);
else if(op==1) update_c(x,y,c);
else printf("%lld\n",query(y));
}
return 0;
}
我的石山唐诗代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 100010
#define M 1010
#define MOD 10007
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pLL pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void writing(i128 x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(i128 x)
{
if(x<0)
{
cout<<'-';
x=-x;
}
writing(x);
}
LL n,op,x,y,kc,ks,L[M],R[M],whe[N];
LL a[N],mu[M],ad[M],c;
LL q(LL l)
{
return (a[l]*mu[whe[l]]+ad[whe[l]])%MOD;
}
void baoli(LL k)
{
rep(i,L[k],R[k],1)a[i]=(a[i]*mu[k]+ad[k])%MOD;
mu[k]=1;
ad[k]=0;
}
void bui()
{
kc=sqrt(n);
ks=n/kc;
if(n%kc!=0)ks++;
rep(i,1,ks,1)
{
L[i]=(i-1)*kc+1;
R[i]=L[i]+kc-1;
mu[i]=1;
}
R[ks]=n;
rep(i,1,n,1)whe[i]=(i-1)/kc+1;
}
void add(LL l,LL r,LL num)
{
LL kl=whe[l],kr=whe[r];
if(kl==kr)
{
baoli(kr);
rep(i,l,r,1)
{
a[i]=(a[i]+num)%MOD;
}
}
else
{
baoli(kl);
baoli(kr);
repn(i,kl+1,kr,1)
{
ad[i]=(ad[i]+num)%MOD;
}
rep(i,l,R[kl],1)
{
a[i]=(a[i]+num)%MOD;
}
rep(i,L[kr],r,1)
{
a[i]=(a[i]+num)%MOD;
}
}
}
void tim(LL l,LL r,LL num)
{
LL kl=whe[l],kr=whe[r];
if(kl==kr)
{
baoli(kr);
rep(i,l,r,1)
{
a[i]=(a[i]*num)%MOD;
}
}
else
{
repn(i,kl+1,kr,1)
{
ad[i]=(ad[i]*num)%MOD;
mu[i]=(mu[i]*num)%MOD;
}
baoli(kl);
baoli(kr);
rep(i,l,R[kl],1)
{
a[i]=(a[i]*num)%MOD;
}
rep(i,L[kr],r,1)
{
a[i]=(a[i]*num)%MOD;
}
}
}
int main()
{
cin>>n;
rep(i,1,n,1)
{
read(a[i]);
a[i]%=MOD;
}
bui();
rep(i,1,n,1)
{
read(op);
read(x);
read(y);
read(c);
c%=MOD;
if(op==0)add(x,y,c);
if(op==1)tim(x,y,c);
if(op==2)
{
write(q(y));
puts("");
}
}
return 0;
}
T8
推平操作咋实现?
用 tag 记录这块被推平的数是啥
两头的不完整块暴力下放 tag 并暴力修改。
查询的话不完整块还是暴力,整块的话拿一个 map 当作桶,记录每个数出现的次数。
推平时把整块的桶清空就行,然后再把推平的值的桶赋值为块长。
本题代码
#include<map>
#include<cmath>
#include<cstdio>
#define rep(i,a,b,g) for(int i=a;i<=b;i+=g)
#define repn(i,a,b,g) for(int i=a;i<b;i+=g)
using namespace std;
int read()
{
int f=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
return x;
}
void writing(int x)
{
if(x>=10)writing(x/10);
putchar(x%10+'0');
}
void write(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
writing(x);
}
int n,ooo,a[100010],whe[100010],L[400],R[400],tg[400],vv[400];
map<int,int>mp[400];
int baoli(int l,int r,int k)
{
int in=whe[l],ans=0;
if(vv[in])
{
vv[in]=0;
rep(i,L[in],R[in],1)a[i]=tg[in];
}
rep(i,l,r,1)
{
mp[in][a[i]]--;
mp[in][k]++;
ans+=(a[i]==k);
a[i]=k;
}
return ans;
}
int sol(int l,int r,int k)
{
int lin=whe[l],rin=whe[r],ans=0;
if(lin==rin)return baoli(l,r,k);
ans+=baoli(l,R[lin],k)+baoli(L[rin],r,k);
repn(i,lin+1,rin,1)
{
ans+=mp[i][k];
vv[i]=1;
tg[i]=k;
mp[i].clear();
mp[i][k]=R[i]-L[i]+1;
}
return ans;
}
int main()
{
n=read();
ooo=sqrt(n);
rep(i,1,n,1)a[i]=read();
rep(i,1,ooo,1)
{
L[i]=R[i-1]+1;
R[i]=i*ooo;
}
R[ooo]=n;
rep(i,1,ooo,1)
{
rep(j,L[i],R[i],1)
{
whe[j]=i;
mp[i][a[j]]++;
}
}
int l,r,k;
rep(i,1,n,1)
{
l=read(),r=read(),k=read();
write(sol(l,r,k));
puts("");
}
return 0;
}