标签：map 队列遍历 int 非线性 include chapter10 元素数据结构

机试中考查的一些非线性数据结构，包括二叉树、二叉排序树、优先队列和散列表。

1.二叉树(Binary Tree)

对于二叉树来说，机试中常考的是其各种遍历方法，分为前序、中序、后序遍历，以及层次遍历。

1.2 二叉树遍历

题目描述+输入输出

题目描述：
二叉树的前序、中序、后序遍历的定义。前序遍历:对任意一棵子树，首先访问根，然后遍历其左子树，最后遍历其右子树;中序遍历:对任意一棵子树，首先遍历其左子树，然后访问根,最后遍历其右子树;后序遍历:对任意一棵子树，首先遍历其左子树，然后遍历其右子树，最后访问根。给定一棵二叉树的前序遍历和中序遍历，求其后序遍历(提示:给定前序遍历与中序遍历能够唯一地确定后序遍历)。

输入：
两个字符串,其长度n均小于等于26。第一行为前序遍历,第二行为中序遍历。
二叉树中的结点名称以大写字母A,B, C,….表示,最多26个结点。

输出：
输入样例可能有多组，对于每组测试样例,输出一行,为后序遍历的字符串。

样例输入：
ABC
BAC
FDXEAG
XDEFAG

样例输出：
BCA
XEDGAF

由前序和中序遍历唯一确定一颗二叉树

//二叉树遍历 2024-03-13
#include <iostream>
#include <cstdio>
#include <string>

using namespace std;

typedef char Elemtype;
typedef struct BiTNode {
    Elemtype data;
    struct BiTNode *leftChild, *rightChild;
}BiTNode, *BiTree;

//用前序遍历和中序遍历唯一确定，建立一颗树(递归实现)
BiTree Build(string preOrder, string InOrder) {
    if(preOrder.size() == 0) {
        return nullptr; //C++的空指针
    }
    Elemtype c = preOrder[0];
    BiTree root = (BiTNode *)calloc(1, sizeof(BiTNode));
    root->data = c;
    int index = InOrder.find(c);
    root->leftChild = Build(preOrder.substr(1, index), InOrder.substr(0, index));
    root->rightChild = Build(preOrder.substr(index + 1), InOrder.substr(index + 1));
    return root;
}

void postOrder(BiTree T) {
    if(T != NULL) {
        postOrder(T->leftChild);
        postOrder(T->rightChild);
        printf("%c", T->data);
    }
}

int main()
{
    string preOrder, inOrder;
    while(cin >> preOrder >> inOrder) {
        BiTree root = Build(preOrder, inOrder);
        postOrder(root);
        printf("\n");
    }
    return 0;
}

2.二叉排序树(Binary Search Tree)

二叉排序树也称二叉搜索树，是一颗特殊的二叉树，具有左结点值 < 根结点值 < 右结点值的特点。如果各个数字插入的顺序不同，那么得到的二叉排序树的形态很可能不同，所以插入顺序对形态有影响。

如果对二叉排序树进行中序遍历，那么其遍历结果必然是一个升序序列，这也是二叉排序树名称的由来。通过建立一颗二叉排序树，就能对原本无序的序列进行排序，并实现序列的动态维护。

建立一棵二叉排序树

//建立一棵二叉排序树，并前序、中序遍历输出这棵树
#include <iostream>
#include <cstdio>

using namespace std;

typedef int Elemtype;
typedef struct BiTNode {
    Elemtype data;
    struct BiTNode *leftChild, *rightChild;
}BiTNode, *BiTree;

//递归建立二叉排序树
void Insert(BiTNode *&T, int x) {
    if(T == NULL) {
        T = (BiTNode *)calloc(1, sizeof(BiTNode));
        T->data = x;
    } else if(x < T->data) {
        Insert(T->leftChild, x);
    } else if(x > T->data) {
        Insert(T->rightChild, x);
    }
    return;
}

void InOrder(BiTree T) {
    if(T) {
        InOrder(T->leftChild);
        printf("%3d", T->data);
        InOrder(T->rightChild);
    }
}

int main()
{
    int n;
    while(cin >> n) {
        BiTree root = NULL;
        int num;
        while(n--) {
            cin >> num;
            Insert(root, num);
        }
        InOrder(root);
        printf("\n");
    }
    return 0;
}

3.-1 优先队列

优先队列（Priority Queue）是指能够将数据按照事先规定的优先级次序进行动态组织的数据结构。在优先队列中，每个元素都被赋予了优先级，访问元素时，只能访问当前队列中优先级最高的元素，即最高级先出规律（First-In Greatest-Out）

优先队列其实是一棵完全二叉树，用二叉堆实现，例如默认是优先级越高越先输出，那么就建立一个大顶堆，进一步可用大顶堆做查询、入队、出队操作。

只需学会使用优先队列的标准模板即可，无需关心实现细节。

3.1 priority_queue定义

要使用模板，先添加头文件#include <queue>，和普通队列头文件一样。定义一个优先队列priorty_queue的写法是priority_queue<typename> name，typename可以是任意的数据类型。

3.2 priority_queue的状态

1、empty()，返回当前优先队列是否为空；
2、size()，返回当前优先队列元素个数。

3.3 priority_queue元素的添加或删除

1、push(elem)，定义一个优先队列后，用于实现元素的入队操作，即添加新元素
2、pop()，实现元素出队操作。

3.4 priority_queue元素的访问

由于优先队列对访问元素的限制，优先队列只能通过top()访问当前队列中优先级最高的元素。

大顶堆.jpg
默认是大顶堆，优先级越高的元素越排在前面。

3.-2 优先队列的应用

3.1 顺序问题

比较复数大小

//2024-03-15 优先队列解决顺序问题，默认是大顶堆，谁优先级大，谁排前面
#include <iostream>
#include <cstdio>
#include <queue>
#include <string>

using namespace std;

struct Complex {
    int real;
    int imag;
    Complex(int r, int i): real(r), imag(i) {}
    bool operator< (Complex c) const {//重新定义复数这个结构体的比较关系
        if(real * real + imag * imag == c.real * c.real + c.imag * c.imag) {
            return imag > c.imag;
        } else {
            return real * real + imag * imag < c.real * c.real + c.imag * c.imag;
        }
    }
};

int main()
{
    int n;
    priority_queue<Complex> myPriorityQueue;
    cin >> n;
    while(n--) {
        string str;
        cin >> str;
        if(str == "Pop") {
            if(myPriorityQueue.empty()) {
                cout << "empty" <<endl;
            } else {
                Complex current = myPriorityQueue.top();
                printf("%d+i%d\n",current.real, current.imag); 
                myPriorityQueue.pop();
                printf("SIZE = %d\n", myPriorityQueue.size());
            }
        } else {
                int a, b;
                scanf("%d+i%d", &a, &b);
                myPriorityQueue.push(Complex(a, b));
                printf("SIZE = %d\n", myPriorityQueue.size());
            }
    }
    return 0;
}

3.2 哈夫曼树

在机试中最常考查优先队列的应用便是哈夫曼树，由于n个带有权值的叶子结点构成的哈夫曼树可能不唯一，所以关于哈夫曼树的机试题往往考察的是求解最小带权路径长度和。

使用优先队列，可以高效地求出集合K中权值最小的两个元素，不过此时需要的是优先值最小的元素，即小顶堆。且注意到除了叶节点权值 x 树高一种计算方法，中间结点累和也可以哦。

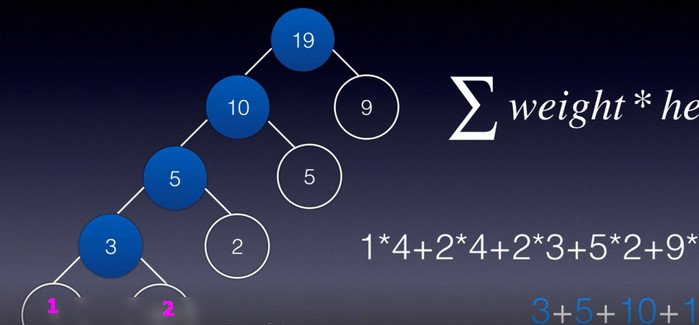
求解最小带权路径长度和

//默认是大顶堆，如何变成小顶堆，即优先级越低越先输出
#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;

int main()
{
    int n;
    cin >> n;
    priority_queue<int, vector<int>, greater<int> > myPriorityQueue;
    for(int i = 0; i < n; ++i) {
        int x;
        cin >> x;
        myPriorityQueue.push(x);
    }
    int answer = 0;
    while(myPriorityQueue.size() > 1) {
        int num1 = myPriorityQueue.top();
        myPriorityQueue.pop();
        int num2 = myPriorityQueue.top();
        myPriorityQueue.pop();
        myPriorityQueue.push(num1+num2);
        answer += num1 + num2;
    }
    cout << answer << endl;
    return 0;
}

4.散列表

散列表是一种根据关键字（key）直接进行访问的数据结构，通过建立关键字和存储位置的直接映射关系(map)，就可以利用关键字直接访问元素，加快查找速度。

学习映射这种思想在机试中的应用。

4.1 标准库-映射模板map

map是一个将关键字（key）和映射值（value）形成一对映射后进行绑定存储的容器。map的底层是用红黑树实现的，内部仍然根据关键字有序，其查找效率仍然为O(logn)。标准库中还有一个无序映射unordered_map容器，其底层是用散列表实现的，其期望的查找效率为O(1)。

4.1.1 map的定义

为使用map容器，要添加头文件#include <map>。定义一个映射map的写法是map<typename T1, typename T2> name，其中tpyename T1是映射关键字的类型，typename T2是映射值的类型。

4.1.2 map的状态

1、empty()，返回当前映射是否为空；
2、size()，返回当前映射元素个数。

4.1.3 map元素的添加或删除

添加新元素，使用insert()
删除已有元素，使用erase()

4.1.4 map元素访问

1、由于map内部重载了[]运算符，因此可以通过```[key]``的方式访问；
2、可以使用at()进行访问;
3、还可以通过迭代器进行访问，迭代器非常类似C语言中的指针，存储地址。

4.1.5 map元素操作

1、find()，查找特定元素，若找到则返回该元素的迭代器，若未找到则返回迭代器end()。注意找到返回的迭代器嗷，要定义一个迭代器接返回值
2、clear()，将映射清空函数。

4.1.6 map迭代器操作

map中常用的迭代器操作有返回映射中首元素迭代器的begin()；以及返回映射尾元素之后一个位置的迭代器end()。

map的定义和操作使用

//标准库中提供的模板-map的使用
#include <iostream>
#include <cstdio>
#include <map>
#include <string>

using namespace std;

map<string, int> myMap;

int main()
{
    myMap["Emma"] = 67;
    myMap["Benedict"] = 100;
    myMap.insert(pair<string, int>("Bob", 77));
    myMap.insert(pair<string, int>("Mary", 98));

    cout << "The score of Mary: " << myMap["Mary"] << endl;
    cout << "The score of Bob: " << myMap.at("Bob") << endl << endl;

    myMap.erase("Benedict");

    map<string, int>::iterator it;   //定义一个迭代器(学习)
    for(it = myMap.begin(); it != myMap.end(); ++it) {
        cout << "the score of " << it->first << ": " << it->second << endl;
    }

    it = myMap.find("Bob");
    if(it != myMap.end()) {
        cout << "Successfully find" << endl;
    } else {
        cout << "Failed find" << endl;
    }

    cout << "the size of myMap: " << myMap.size() << endl;

    myMap.clear();
    return 0;
}

标签：map,队列,遍历,int,非线性,include,chapter10,元素,数据结构
From： https://www.cnblogs.com/paopaotangzu/p/18071605

chapter10-非线性数据结构