深度学习入门
ch03:神经网络
激活函数:
定义:会将输入信号的总和转换为输出信号
$$ {a = b + w1x1 + w2x2 }
a = b + w1x1 + w2x2
y = h(a)
$$
即计算每一元素与其权重乘积及偏置总和的函数
sigmoid函数:
代码实现:
def sigmoid(x):
return 1 / (1 + np.exp(-x)
公式:h(x)=i/(1+exp(-x)),exp(-x)表示为e ^-x
t = np.array([1.0, 2.0, 3.0])
>>> 1.0 + t
array([ 2., 3., 4.])
>>> 1.0 / t
array([ 1. , 0.5 , 0.33333333]
上述为sigmoid函数的运算。
由公式及图像观察到无论x多大,h(x)恒小于0并且其取值只会在0和1区间内,在其左右端点,h(x)趋向于0和1。
阶跃函数
代码实现(支持Numpy版本):
def step_function(x):
y = x > 0
return y.astype(np.int)
由于感知机只接收0和1两个值,阶跃函数只有0和1两个取值,能很好的实现数据的传递。在阶跃函数代码实现中,可以使用不等号运算:
x = np.array([-1.0, 1.0, 2.0])
y = x > 0
print(y)
#array([False, True, True], dtype=bool)
对NumPy数组进行不等号运算后,数组的各个元素都会进行不等号运算, 生成一个布尔型数组,x>0输出转化为True,x<0输出转化为False,并且将输出结果全部放入新数组y中。如果想要数字表达,可以使用astybe方法,即y = y.astype(np.int),将布尔型转化为int型,True会转换为1,False会转换为0。

ReLu(Rectified Linear Unit)函数:
代码实现:
def relu(x):
return np.maximum(0, x)
ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输 出0。
非线性代数:
阶跃函数和sigmoid函数还有其他共同点,就是两者均为非线性函数,非线性代数就是不满足y=kx图像的函数深度学习中使用非线性代数是为了发挥叠加层所 带来的优势,激活函数必须使用非线性函数。假设y(x)=kx,经过n层神经网络计算后,输出为(kx)^n,仅仅只是一次乘法运算,并没有体现深度学习中隐藏的神经网络,无法发挥多层网络带来的优势
多层数组运算:
Numpy中多维数组可以类比数学的矩阵,不同的是数组具有维度,获取数组维度可通过np.dim()函数
获取数组的形状可采用shape实例变量。
>>> B = np.array([[1,2], [3,4], [5,6]])
>>> print(B)
[[1 2]
[3 4]
[5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)
与矩阵不同,多维数组延续python数组的思维,索引从第零维开始
矩阵乘法:
矩阵中横向排列称为行,纵向排列称为列,即常说的横成排,竖成列。
矩阵的乘积是通过左边矩阵的行(横向)和右边矩阵的列(纵 向)以对应元素的方式相乘后再求和而得到的。并且,运算的结果保存为新 的多维数组的元素。
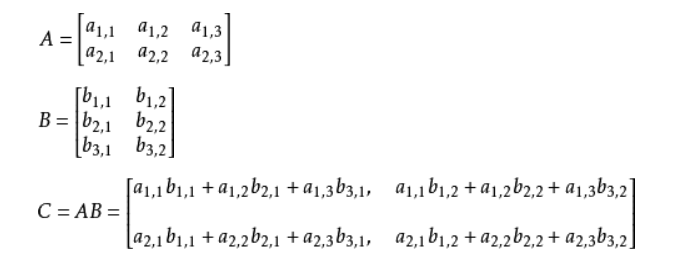
C11即A的第一行与B的第二行相乘,C21即A的第一行与B 的第一轮相乘,以此类推可得到矩阵C
>>> A = np.array([[1,2], [3,4]])
>>> A.shape
(2, 2)
>>> B = np.array([[5,6], [7,8]])
>>> B.shape
(2, 2)
>>> np.dot(A, B)
array([[19, 22],
[43, 50]]
A与B的矩阵乘法可用Numpy的np.dot()进行矩阵运算,但np.dot(A,B)和np.dot(B,A)得到的矩阵右不同,参考线性代数矩阵乘法的左行右列。
tip:矩阵A的第1维的元素个数(列数) 必须和矩阵B的第0维的元素个数(行数)相等
若A的shape为(2,3),则B的shape为(3,n)
但是A的第一维度元素个数必须和B的第0维元素个数相等,同时,A与B相乘得到的C的形状为(2,n)
矩阵C的形状是由矩阵A的行数 和矩阵B的列数构成的,当B为(3,)时,C的形状为(2,)即只有一个维度。
>>> X = np.array([1, 2])
>>> X.shape
(2,)
>>> W = np.array([[1, 3, 5], [2, 4, 6]])
>>> print(W)
[[1 3 5]
[2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X, W)
>>> print(Y)
[ 5 11 17]
上述代码即为神经网络对矩阵乘法内积的运算。
各层间信号传递的实现
在输出层方面,一般地,回 归问题可以使用恒等函数,二元分类问题可以使用 sigmoid函数, 多元分类问题可以使用 softmax函数。
softmax函数:
可以类比数学统计的加权值和概率。
在使用softmax函数时,当电脑遇到超大值运算时,结果会出现不确定的情况,这需要我们引入一个参量C把数字变小,通常情况下会遍历整个数据库,选择最大的数作为参量C然后导入到指数,这样就姮好的降了指数,让计算结果更为精确,同时,加上或减去某个常数并不会改变输出的yk值。
以上就为改进部分。
softmax函数输出的值和为1,这是softmax函数的一个特性,通过这个特性我们可以得到某个结果的概率,在后面的学习中softmax函数还可以运用到学习过程中,调整参数。
手写数字识别:
手写数字识别是深度学习的敲门砖。
load_mnist函数以“(训练图像 ,训练标签 ),(测试图像,测试标签 )”的 形式返回读入的MNIST数据。此外,还可以像load_mnist(normalize=True, flatten=True, one_hot_label=False) 这 样,设 置 3 个 参 数。(摘自书本71页)
第 1 个参数 normalize设置是否将输入图像正规化为0.0~1.0的值。如果将该参数设置 为False,则输入图像的像素会保持原来的0~255。
第2个参数flatten设置 是否展开输入图像(变成一维数组)。如果将该参数设置为False,则输入图 像为1 × 28 × 28的三维数组;若设置为True,则输入图像会保存为由784个 元素构成的一维数组。
第3个参数one_hot_label设置是否将标签保存为onehot表示(one-hot representation)。one-hot表示是仅正确解标签为1,其余 皆为0的数组
一些解释:
参量解释:
在mnist库中,图片的像素为28*28,图片可抽象的理解为三维变量即(sample,weight,height),这是图片的表达。将图片每个像素点作为一个输入,那么就会有784个输入节点,隐藏层有两层,作为像素处理。最后由于输出的结果有0~9总共10种结果,于是输出就会有10个节点。
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p = np.argmax(y) # 获取概率最高的元素的索引
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" ++str(float(accuracy_cnt) / len(x)))
以上是获得最大概率的结果作为输出值,使用的函数时np.argmax()。
normalize是正则化的表达,将每个像素值除以255,将每个数据控制在0~1之间,也称数据白化。
批处理:
上图是输入一个28*28的二维数组,可以看到最后有一个由10个元素构成的一维数组。在Python中可以一次性打包100个图像输入得到结果是这一百个图像输出的数组。
如图。最后我们得到一个(100,10)的二维数组,第一个维度是100个图像的索引值,第二个维度是各图像所得结果的概率。
>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6],
... [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1)
>>> print(y)
[1 2 1 0]
代码实现如上。
在argmax()中,我们引入axis作为沿着第1维方向(以 第1维为轴)找到值最大的元素的索引(第0维对应第1个维度)。
tip:矩阵的第0维是列方向,第1维是行方向。
ch04:神经网络的学习
通过作者的说法,我们可以了解到计算机在学习过程中延续的是人的思维,通过特征量,人可以通过经验常识判断事物,机器学习也有监督学习,当人们将特征量告诉计算机,计算机通过特征量学习。当没有特征量,计算机将从海量的数据不断地调试参数,最后得到一个结果,这就是无监督学习,深度学习个人认为大部分是在有监督地学习。
一些概念:
训练数据和测试数据:
机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和 实验等。首先,使用训练数据进行学习,寻找最优的参数;然后,使用测试 数据评价训练得到的模型的实际能力。
通过训练数据和测试数据,我们可以得到一个具有泛化能力模型,泛化能力是指处理未被观察过的数据(不包含在训练数据中的数据)的 能力,这是机器学习的终极目标。如果仅仅用一个数据学习,往往会出现过拟合的情况,即模型只对训练数据有用,而对其他测试数据作用较小,这是我们不希望看到的。
损失函数:
神经网络学习的过程中,模型通过某个指标表示现在的转态,并以此为线索寻找最优权重参数,这个指标就是损失函数。一般用均方误差和交叉熵误差。
均方误差:
这里,yk是表示神经网络的输出,tk表示监督数据,k表示数据的维数。
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
这是我们手写数字识别某个图片的输出函数及其测试数据,数组y是sigmoid函数的输出值,表示概率。t是监督数据,将正确解标签设为1,其他均设为0,这种表示方法称为one_hot表示。
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2
这是均方误差的代码实现。
交叉熵误差:
其中tk只有正确的标签计为1,其余即为0.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
代码实现如上。这里我们引入了一个参量delta,为了防止log函数出现过小值,这时我们引入一个微小值作为保护性措施。
mini-batch
计算损失函数时,我们要求的是数据的误差总和,这时我们要对其求和,以下是交叉熵误差的平均损失函数。
其实就是将每个输出的交叉熵误差求和,然后除以数据总量,最后得到一个平均交叉熵误差,与之前的正规化相似。
像MNIST中的训练数据有60000个,一一计算太过冗杂,我们可以采用mini-batch学习,从这60000个数据随机抽取若干笔作为学习对象,这就是mini-batch学习。
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
从这60000个数据取10个数据,并记录其索引值,代入循环然后进行学习。
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
上述就是交叉熵误差代码的实现
tip:关于为什么要设定损失函数?
神经网络的学习中,我们最关心的就是权重参数,我们把视线放在某个权重参数并对其求导,若导数为负,这时应将权重往正方向调,反之则应往负方向调,总而言之,调整方向总是与损失函数相反,直至损失函数值为零,为零时,权重的参数将不会更新,最后停留并输出。
采用损失函数作为指标,而不采用识别精度是因为在训练过程中调整参数后,其并不会像sigmoid函数那样连续变化,反而呈现离散,不连续的值,相反,以损失函数为指标,能够发生连续的变化。所以,回归之前的阶跃函数,与线性函数,我们发现线性函数的导数恒为一个常数,此时学习没有意义,只是简单的数学运算;而阶跃函数在瞬间变化且只变化一次,不能很好地反映学习过程,所以sigmoid函数既连续光滑,又能将输出值限定在0~1内,所以在输出层常用sigmoid函数。
数值微分
高等数学中我们常用求导来求函数的变化率,无论取值我们都能得到一个较为精确的值,但在计算机内,过小的值会舍入误差,输出为0.0,下面是一个例子。
>>> np.float32(1e-50)
0.0
所以我们引入了数值差分,计算f(x+h)和f(x-h)之间的差分,而我们用数学方法求的微分与真实的函数往往有很大的差别,而中心差分(也称前后差分)能够减小误差。
偏导数
下面我们以函数f(x0,x)=x02+x2为例对函数进行偏导数计算,首先使用作图软件作出其三维函数图像。
通过函数式可以发现有两个变量,各自影响函数取值,对多个变量求导称为偏导数。
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
对于某个有特定的点,已知某个数便可求其偏导数
梯度(gradient):
定义:像 (df/dx0,df/dx)这样的全部变量的偏导数汇总而成的向量就叫梯度。
还是以上一节的函数为例子,作出梯度图。
通过图像可以发现梯度都指向函数的最低处,且离最低点越远,箭头越大,这表示下降得越快。但箭头方向并不是指向最低点,实际上箭头指向的是下降最快的地方,即导函数绝对值最大的方向。
神经网络在学习中必须找到最优参数(权重和配置),这使得损失函数取得最小值。可是在某点其空间内其张量是不定的,通过梯度上升或下降的方法求得的函数最小值就是梯度法。
在函数中,鞍点指的是函数的极小值或者是最小值,在鞍点出,函数的梯度为0。不论是求函数的最大值还是最小值,梯度法都是不二之选,不过求最大值就是梯度上升法,求最小值就是梯度下降法。在深度学习中,由于我们的目的是使的损失函数达到最小值,我们可以用数学式子来表述梯度法

上式中,我们引入了一个参量η,我们叫它学习率,学习率决定学习的数量以及多大程度上更新参数。
一般的,像学习率这种人为规定的参量我们称之为超参量,而机器从海量数据中学的权重参数和偏置这种就不是超参量,是通过训练 数据和学习算法自动获得的。

上图阴影点就是梯度法不断靠近最低点,随着学习的深入,损失函数不断向最小值靠近。
学习率过大或过小都会影响最后的结果,过大会使得结果发散成一个很大的值;过小会使得结果没怎么更新就结束了,这使得我们的学习变得没有意义。
神经网络的梯度:
在神经网络的学习过程中,我们要处理的往往是一堆数据,大多是以矩阵的方式输入数据,这时我们会用下面的方式进行矩阵运算:
我们引入一个叫simplenet的类计算矩阵的梯度(在代码库中)其中包含predict和loss函数,表示预测和计算损失函数.同样的,梯度计算也会放回对应的参数值,如果参数为正就要往负方向调整,为负就往正方向调整,数值的绝对值大小反映其对函数的贡献大小。
神经网络算法的实现:
SGD:
神经网络的学习步骤大体可分为以下几步:
前提:神经网络存在合适的权重和偏置
步骤一(mini-batch):
从训练数据中随机抽取部分数据作为训练数据,并将其传达到最后的loss函数,而神经网络学习的目的就是要减小损失函数知到大小。
步骤二(gradient):
为了达到神经网络学习的目的,要进行各权重参数的梯度,而梯度就是损失函数下降最快的方向。
步骤三(update):
在计算出各权重参数的梯度后,我们会通过返回的loss函数值进行调整和更新。
步骤四(again and again ):
重复步骤一,步骤二,步骤三。直至梯度不再更新。
这种方法就叫做随机梯度下降法,简称SGD,即stochastic gradient descent的首字母。
两层神经网络的实现:
见代码。
评价神经网络的学习:
评价一个神经网络模型主要是评价一个模型的学习能力和其泛化能力。而泛化能力就是要在模型未接触过的数据中进行运算。如果一个模型的泛化能力不高就会产生负面的效果:过拟合。过拟合是指,虽然训练数据中的数字图像能 被正确辨别,但是不在训练数据中的数字图像却无法被识别的现象。
函数库
ReLu函数
def relu(x):
return np.maximum(0, x)
softmax函数:
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
均方误差
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
交叉熵误差:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_sizedef cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
数值微分
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
计算梯度
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同的数组
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
np.zeros_ like(x)会生成一个形状和x相同、所有元素都为0的数组
梯度下降法:
def gradient_descent(f, init_x, lr=0.01, step_num=100):#init_x是初始值,lr是学习率learning
rate,step_num是梯度法的重复次数
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
矩阵的梯度计算:
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3) # 用高斯分布进行初始化
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t) return los
两层神经网络:
import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,#参数从头开始依次表示输入层的神经元数、隐藏层
的神经元数、输出层的神经元数
weight_init_std=0.01):
# 初始化权重
self.params = {}#保存神经网络的参数的字典型变量
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):#进行识别(推理),参数x是图像数据.
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):#计算损失函数的值。参数x是图像数据,t是正确解标签(后面3个方法的参数也一样)
y = self.predict(x)
return cross_entropy_error(y, t)#使用的办法时交叉熵误差
def accuracy(self, x, t):#计算识别精度
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):#计算权重参数的梯度,也可采用反向传播的办法。
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
