分析
出得很好,模板套模板,希望下次再来。
难点在于维护最后连续喝的 DS 饮料数量。设这次喝原味饮料的区间为 \([l,r]\),上一次为 \([l',r']\)。则有两种情况:
- \([l,r]\) 与 \([l',r']\) 不相交。如:
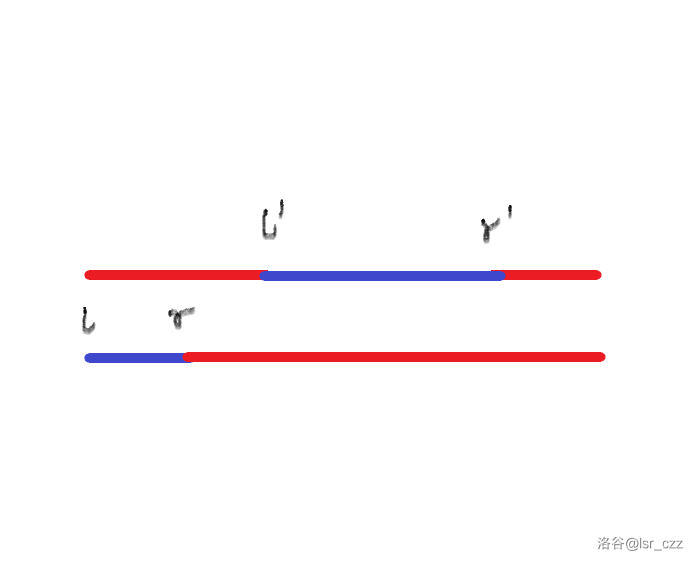
在 \([l',r']\) 和 \([l,r]\) 两个区间中的 DS 连续喝的同种饮料数量都会变成 \(k\),而其他的则增加 \(k\)。
- \([l,r]\) 与 \([l',r']\) 相交。如:
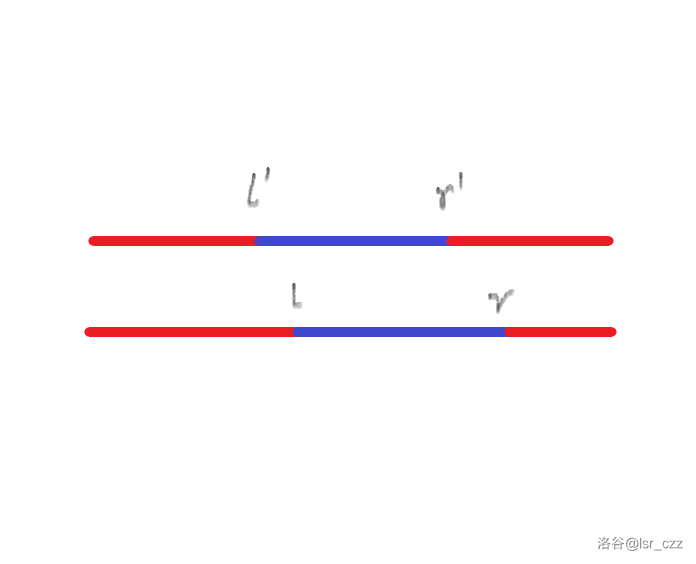
在 \([l',r']\) 和 \([l,r]\) 两个区间中不相交的区间的 DS 连续喝的同种饮料数量都会变成 \(k\),而其他的则增加 \(k\)。
这就是操作一转化之后你能维护的东西。说是模板其实是因为这个区间赋值和区间加就是扶苏的问题。这里就不分析了。
然后就是另一个模板——维护操作二。很明显的一个小清新,因为 DS 的数量不增。考虑线段树上的某个区间在什么情况下会有 DS 被干掉。因为 BTC 是干掉连续喝相同饮料数量不少于 \(k\) 的,所以维护一个区间最大值,若最大值 \(x \ge k\) 且该区间有 DS 没被干掉时,这个区间有很大可能发生 DS 被 BTC 干掉的情况。很简单的模板小清新,单点修改即可。
对于询问,就是求出来区间 \([1,n]\) 有多少 DS 被干掉了,答案为 \(n-cnt\)。求序列被干掉的 DS 数量可以 \(O(1)\)。
复杂度 \(O(n \log n)\)。
小细节:保证小清新的时间复杂度,当一个 DS 被干掉之后,他的最大值应赋值为极小值。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define re register
#define il inline
#define pii pair<int,int>
#define x first
#define y second
#define gc getchar()
#define rd read()
#define debug() puts("------------")
namespace yzqwq{
il int read(){
int x=0,f=1;char ch=gc;
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=gc;}
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=gc;
return x*f;
}
il int qmi(int a,int b,int p){
int ans=1;
while(b){
if(b&1) ans=ans*a%p;
a=a*a%p,b>>=1;
}
return ans;
}
il auto max(auto a,auto b){return (a>b?a:b);}
il auto min(auto a,auto b){return (a<b?a:b);}
il int gcd(int a,int b){
if(!b) return a;
return gcd(b,a%b);
}
il int lcm(int a,int b){
return a/gcd(a,b)*b;
}
il void exgcd(int a,int b,int &x,int &y){
if(!b) return x=1,y=0,void(0);
exgcd(b,a%b,x,y);
int t=x;
x=y,y=t-a/b*x;
return ;
}
mt19937 rnd(time(0));
}
using namespace yzqwq;
const int N=3e5+10;
int n,q;
pii lst;
struct Tree{
int l,r;
int mx,kil;
int tag1,tag2,tag;
}tr[N<<2];
il void up(int now){
tr[now].mx=max(tr[now<<1].mx,tr[now<<1|1].mx);
tr[now].kil=tr[now<<1].kil+tr[now<<1|1].kil;
return ;
}
il void down(int now){
if(tr[now].tag==1){//覆盖
tr[now<<1].tag1=tr[now<<1|1].tag1=tr[now].tag1;
tr[now<<1].tag2=tr[now<<1|1].tag2=tr[now].tag2;
tr[now<<1].mx=tr[now<<1|1].mx=tr[now].tag1+tr[now].tag2;
tr[now].tag1=tr[now].tag2=tr[now].tag=0;
tr[now<<1].tag=tr[now<<1|1].tag=1;
}
else{//加
tr[now<<1].tag2+=tr[now].tag2,
tr[now<<1|1].tag2+=tr[now].tag2;
tr[now<<1].mx+=tr[now].tag2,
tr[now<<1|1].mx+=tr[now].tag2;
tr[now].tag1=tr[now].tag2=tr[now].tag=0;
}
return ;
}
il void build(int now,int l,int r){
tr[now].l=l,tr[now].r=r;
if(l==r) return ;
int mid=l+r>>1;
build(now<<1,l,mid),build(now<<1|1,mid+1,r);
return ;
}
il void add1(int now,int l,int r,int k){//区间加
if(tr[now].l>=l&&tr[now].r<=r){
tr[now].mx+=k,
tr[now].tag2+=k;
return ;
}
down(now);
int mid=tr[now].l+tr[now].r>>1;
if(l<=mid) add1(now<<1,l,r,k);
if(mid<r) add1(now<<1|1,l,r,k);
return up(now),void(0);
}
il void add2(int now,int l,int r,int k){//区间覆盖
if(tr[now].l>=l&&tr[now].r<=r){
tr[now].mx=tr[now].tag1=k,
tr[now].tag2=0,tr[now].tag=1;
return ;
}
down(now);
int mid=tr[now].l+tr[now].r>>1;
if(l<=mid) add2(now<<1,l,r,k);
if(mid<r) add2(now<<1|1,l,r,k);
return up(now),void(0);
}
il void del(int now,int l,int r,int k){//干掉 DS
if(tr[now].l==tr[now].r){
tr[now].mx=-1e18,tr[now].kil=1;
return ;
}
down(now);
int mid=tr[now].l+tr[now].r>>1;
if(l<=mid&&tr[now<<1].mx>=k&&tr[now<<1].kil<tr[now<<1].r-tr[now<<1].l+1) del(now<<1,l,r,k);
if(mid<r&&tr[now<<1|1].mx>=k&&tr[now<<1|1].kil<tr[now<<1|1].r-tr[now<<1|1].l+1) del(now<<1|1,l,r,k);
return up(now),void(0);
}
il void solve(){
n=rd,q=rd;
build(1,1,n);
for(re int i=1;i<=q;++i){
int op=rd,l,r,k;
if(op==1){
l=rd,r=rd,k=rd;
if(!lst.x) add1(1,1,n,k),lst={l,r};
else{
int l_=lst.x,r_=lst.y;
if(r_<l||r<l_){//区间不相交
if(min(l,l_)>1) add1(1,1,min(l,l_)-1,k);
if(max(r,r_)<n) add1(1,max(r,r_)+1,n,k);
add2(1,l_,r_,k);
add2(1,l,r,k);
if(r_<l&&r_+1<=l-1) add1(1,r_+1,l-1,k);
if(r<l_&&r+1<=l_-1) add1(1,r+1,l_-1,k);
}
else{//区间相交
if(min(l,l_)>1) add1(1,1,min(l,l_)-1,k);
if(max(r,r_)<n) add1(1,max(r,r_)+1,n,k);
add2(1,min(l,l_),max(l,l_)-1,k);
add2(1,min(r,r_)+1,max(r,r_),k);
add1(1,max(l,l_),min(r,r_),k);
}
lst={l,r};
}
}
else if(op==2){
l=rd,r=rd,k=rd;
del(1,l,r,k);
}
else printf("%lld\n",n-tr[1].kil);
}
return ;
}
signed main(){
int t=1;while(t--)
solve();
return 0;
}