暑假（4）

NOIP2023模拟测试赛（十九）

A

假设询问 \((u,v)\)，\(u,v\) 间距离为 \(d\)。

首先如果 \(k+1\le d\) 则两人怎么走都不会相遇，答案即 \(k\bmod2\)。现在 \(k+1>d\)。

对 \(d,k\) 的奇偶性分类讨论，如下图：

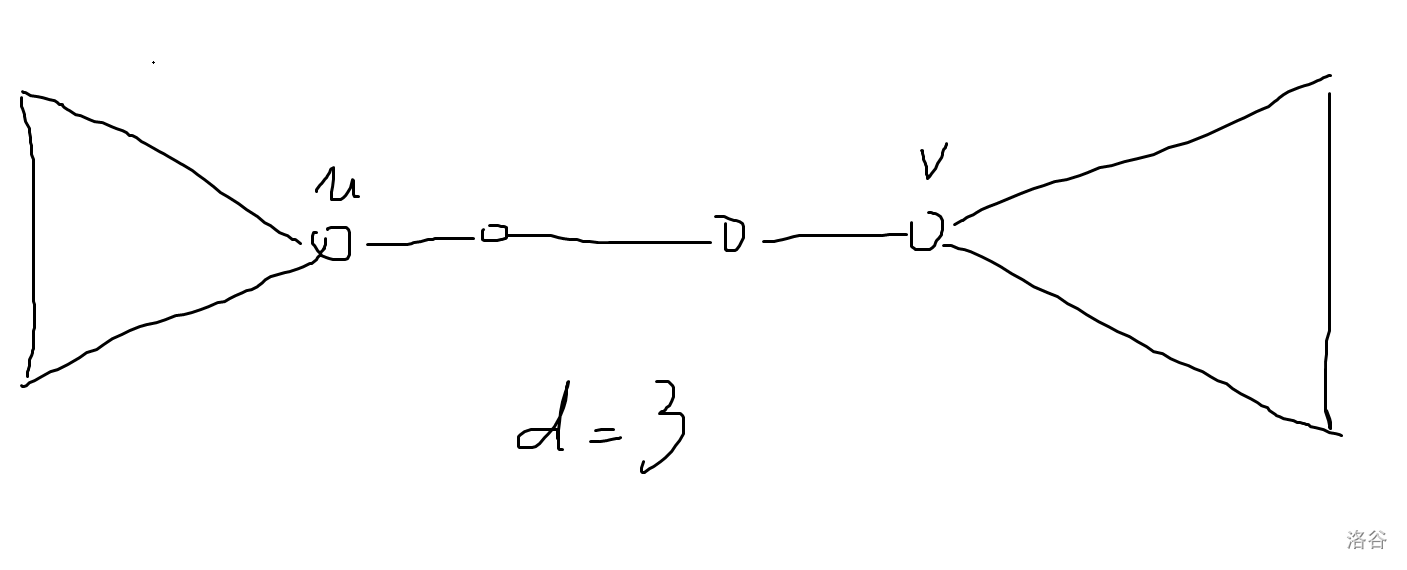
• 当 \(d\) 为奇数，\(k\) 为偶数时：（例如上图 \(d=3,k=4\)）

容易发现答案为 \(0\)。因为两人可以向对方方向走，且两人都不能使答案更偏向于自己：如果不往对面走，会面临自己的点被占领而自己下一步不能占回来的情况。

• 当 \(d\) 为奇数，\(k\) 为奇数时：（例如上图 \(d=3,k=3\)）

由于先手多走一步，在 \(k-1\) 步之前，双方都能保持占领的区域面积相同；但第 \(k\) 步如果后手让先手占领自己原先占领的区域，会导致 \(A-B\) 再加 \(1\)。

因此后手希望找到一个路径，使得先手最后一步只能占领未被占领的区域，这样答案为 \(1\)。

除此之外，后手走的路径还要不重复，否则不能保证前 \(k-1\) 步占领的区域与先手一样多。

如何判断是否有这么一条路径？先手总共走 \(\frac{k+1}2\) 步。根据上面的推断，先手会沿着 \(u,v\) 的路径一直向 \(v\) 走 \(\frac{k+1}2\) 步，以尽量限制后手所走路径的范围。

如果 \(d\le\frac{k+1}2\)，先手一定能到 \(v\)，后手无路可逃。否则，求出 \(u\) 向 \(v\) 方向走 \(\frac{k+1}2\) 步到达的点 \(w\)。那么后手只能在 \(w\) 以右行动。

那么就是要求，\(w\) 右侧的所有点到 \(v\) 的最大距离，判断这个距离是否 \(\ge\frac{k-1}2\)。

到 \(v\) 距离最大的点一定是这些点的直径端点之一。

那么就是要维护，\(w\) 右侧形成的子树的直径。

直径可以合并，发现 \(w\) 右侧的点在 \(dfn\) 区间上要么是一段子树的 \(dfn\) 区间要么是 \([1,n]\) 挖去一段 \(dfn\) 区间。

可以线段树或者 st 表等维护区间直径。复杂度视实现 \(\mathcal O(n\log n)\) 或者 \(\mathcal O(n\log^2n)\)。

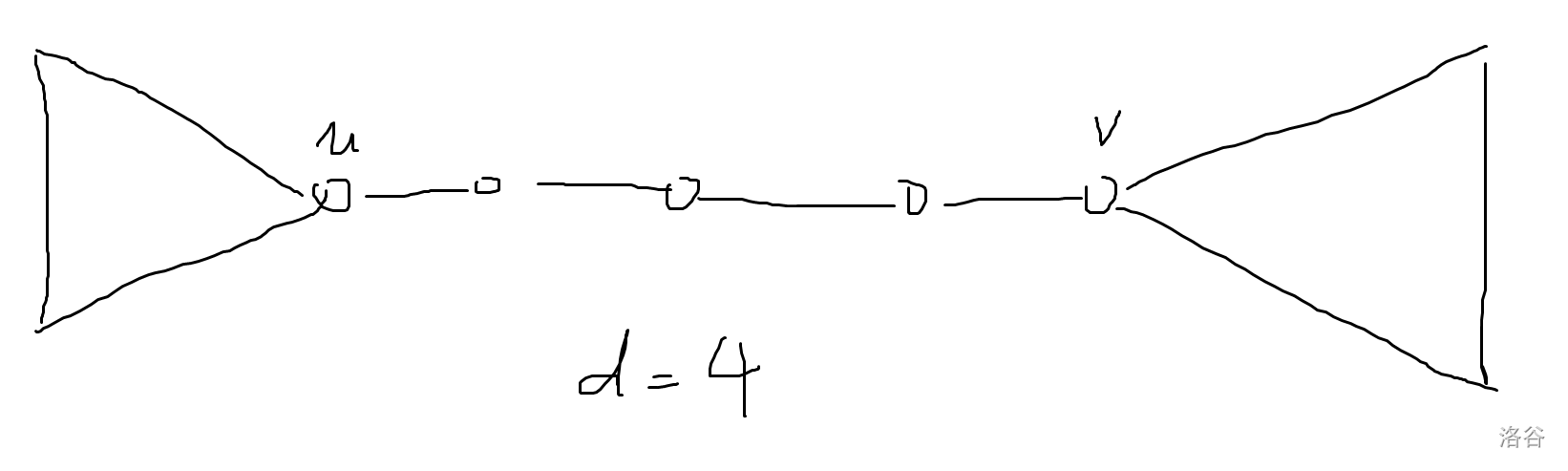
• 当 \(d\) 为偶数，\(k\) 为偶数时：（例如上图 \(d=4,k=4\)）

这里后手的最后一步可能会比先手多踩掉一个先手的点。这样答案为 \(-1\)。

先手不希望这样，那么就用上面第二类的类似方法求先手能否让答案变为 \(0\)。

• 当 \(d\) 为偶数，\(k\) 为奇数时：（例如上图 \(d=4,k=5\)）

答案为 \(1\)。会发现先手后手都无法改变这个结果。

B

匪夷所思，打个表会发现必败态很少的，而且形成两条近似直线的东西，斜率趋近于 \(\varphi=\frac{\sqrt{5}-1}2\)，\(\hat\varphi=\frac{\sqrt{5}+1}2\)。

大胆猜测第 \(i\) 个点就是 \(\lfloor\varphi n\rfloor\) 之类的，然后发现是真的，可能因为初始三个点位置不太对要判一下，，，

然后你直接除一个 \(\varphi\) 是不行的，会掉精度，可以二分

然后求必胜态的走法，下面左边左下角分别搞一下，下、左边什么的都可以二分，左下方会发现 \(y-x\) 即是编号。

然后还是过不了，发现 long double 精度不够，手写个高精度就过了，如果位数太多乘法还会 TLE。？

C

NOIP2023模拟测试赛（二十）

A

如果没有修改操作，考虑莫队，记录区间的所有不同的 \(cnt\)，这个级别是 \(\mathcal \Theta(\sqrt n)\) 的！！

然后每次询问把 \(cnt\) 排个序，扫一下每个长度为 \(k\) 的区间，复杂度是 \(\Theta(\sqrt n\log n)\) 的。

这样复杂度是 \(\Theta(n\sqrt n\log n)\) 的，如果视 \(n,m\) 同阶。

考虑修改，直接带修莫队，复杂度 \(\Theta(n^{\frac53}+n\sqrt n\log n)\)。

B

对于一个选择的方案，我们可以对每个选了的数计算贡献，贡献是它的值乘上包含它且不包含下一个数的区间个数。

dp：设 \(dp_i\) 表示最后一个选 \(i\) 的答案。由于 \(i\) 的贡献和下一个选的数有关，我们在 \(dp_i\) 中不计算 \(i\) 的贡献。

转移，考虑枚举上一个选的数 \(j\)。\(dp_j\) 中没有计算 \(j\) 的贡献，现在算 \(j\) 的贡献。

\(j\) 的贡献是 \(a_j\times s_j\)，\(s_j\) 为满足 \(l\le j\le r<i\) 的题目中区间 \([l,r]\) 个数，即包含 \(j\) 但不包含 \(i\)。

将题中的 \([l,r]\) 按 \(r\) 排序，扫描线在 \(r\) 处加入 \(l\)，即将 \([1,l]\) 的 \(s\) 加 \(1\)。

那么就是求 \(\min_j\{a_js_j+dp_j\}\)。\(a_j\) 看作斜率，\(dp_j\) 看作截距，这些都只会单点修改。

\(s_j\) 是自变量，每次区间加 \(1\)。要求最小值的话，可以直接 KTT 维护。

复杂度目前为 \(\mathcal O(n\log^3n)\)。

C

扫描线，维护 \(i\) 到前面所有点的答案。

加入一个数，前驱后继分开算，对于前驱，考虑一个暴力算法：从 \(i\) 开始跳，每次找当前点 \(x\) 前的第一个比 \(a_x\) 大的，比 \(a_i\) 小的数，用它更新答案。

这样最多跳 \(\Theta(n)\) 次，不可以。考虑对于当前一个 \(x\)，若跳到的点 \(a_y\) 满足 \(a_y-a_x\le a_i-a_y\) 则 \(y\) 肯定不优。

那么我们只跳 \(x\) 之前第一个 \(y\) 满足 \(a_y\in(\frac12(a_i+a_x),a_i)\)，这样每次限制区间减半，最多跳 \(\Theta(\log n)\) 次。

线段树维护答案，主席树维护最大的 \(y\)，复杂度 \(\Theta(n\log^2n)\)。

NOIP2023模拟测试赛（二十一）

A

路径形状是第一行一段前缀，加上第二行对应的后缀。设 \(w_i\) 表示在第 \(i\) 行向下走的权值，即 \(pre_{1,i}+suf_{2,i}\)。

假设第一行有两个数 \(a_{1,i}>a_{1,j}\)，考虑交换它们：\(w_{1\sim i-1}\) 及 \(w_{j\sim n}\) 不会受到影响，\(w_{i\sim j-1}\) 会全部减 \(a_{1,i}-a_{1,j}\)。

所以换了一定更优，因此答案中第一行一定递增，第二行一定递减。

然后发现，\(w_{i}=w_{i-1}+a_{1,i+1}-a_{2,i}\)，由于 \(a_{1,i+1}\) 递增，\(a_{2,i}\) 取反也递增，因此 \(w_i-w_{i-1}\) 递增。

所以 \(w\) 下凸，最大值一定在 \(w_1\) 或者 \(w_n\) 取到。

然后又发现，设全部最小值是 \(mn\)，次小值是 \(sec\)，假设 \(mn\) 在 \(a_{1,1}\)。

那么如果 \(sec\) 不在 \(a_{2,n}\)，它一定在 \(a_{1,2}\)。交换 \(a_{2,n}\) 和 \(a_{1,2}\)，则 \(w_n\) 不变，但 \(w_1\) 可能会变小。

所以 \(mn,sec\) 分别是第一行第二行最小值。

剩下就好办了，想让 \(w_1,w_n\) 最大值最小，即 \(\max\{mn+sec+\sum_{i\not=1} a_{1,i},mn+sec+\sum_{i\not=n} a_{2,i}\}\) 最小。

\(mn+sec\) 提出来，剩下就分两堆 \(n-1\) 的求最大值最小。

直接背包即可。有人说过不去，要用 bitset 优化。但是我剪个枝就过了欸。

复杂度 \(\Theta(n^3V)\)。

B

建圆方树，每个方点开 multiset 维护儿子的所有权值最小值，查询注意如果 lca 是方点还要把它父亲也算了。

注意1：multiset 删除如果直接 s.erase(val) 会把所有相同的删了。要 s.erase( s.find(val) )

注意2：tarjan的时候，想把 \(v\) 的子树 pop 出来建方点，不可以 pop 直到 \(u\) 因为 \(u,v\) 在栈里不相邻。要 pop 直到 \(v\)

C

考虑线段树，如果求出每个初值 \(x\) 走过当前区间得到的结果，那么直接走 \(\log\) 次即可得到答案。

走过一个长度为 \(len\) 的区间，最后答案一定是某个 \(sum-p\times i\)，这里 \(sum\) 是区间 \(a\) 之和，\(i\in[0,len]\)。

如果求出走过区间要减多少次 \(p\) 就好了。容易发现，最终要减 \(i\) 次的所有可能初值形成一段区间。

假设减 \(i\) 次的区间左端点为 \(c_i\)。则第 \(i\) 个区间为 \([c_i,c_{i+1})\)，查询直接求在哪个区间中即可。

即每个区间会有一个分段函数，现在要维护这个分段函数。

现在考虑求 \(c\)。对于线段树上节点 \(u\)，用左右儿子 \(ls,rs\) 的 \(c\) 求 \(u\) 的 \(c\)。

考虑一个暴力算法，要求 \(c_{u,i}\)，枚举 \(j+k=i\)，即在左区间减了 \(j\) 次 \(p\)，右区间减了 \(k\) 次 \(p\)，一共就减了 \(i\) 次 \(p\)。

什么时候 \(c_{ls,j},c_{rs,k}\) 能转移到 \(c_{u,i}\)？至少需要初始值走过左区间得到的值大于右边的初始值要求。

可以把最大的左边初始值带进去检测，即检测 \(c_{ls,j+1}-1+sum_{ls}-jp\) 是否 \(\ge c_{rs,k}\)。

如果满足这个条件，则考虑求此时最小初始值，贡献进 \(c_{u,i}\)。初始值 \(x\) 需要满足：

• \(x\ge c_{ls,j}\)。

• \(x+sum_{ls}-jp\ge c_{rs,k}\) 即 \(x\ge c_{rs,k}-sum_{ls}+jp\)。

两个限制取最大值即是 \(x\) 最小值。这样暴力转移是 \(\Theta(n^2)\) 的。

注意到一个性质，对于 \(c\) 有 \(c_i\ge c_{i-1}+p\)。

证明考虑有 \(c_i> c_{i-1}-1+p\)，因为 \(c_{i-1}-1\) 带入函数中会减 \(i-2\) 次 \(p\)，如果加了 \(p\) 算，则前面若干次减 \(p\) 的运算都与不加一样，第一个不减 \(p\) 的运算会减 \(p\)，剩下的又是一样的。

所以减 \(p\) 的次数只会加 \(1\)，自然就到不了减 \(i\) 次的界限 \(c_i\)。

现在我们枚举 \(i\) 再枚举 \(j\)，考虑 \(j\) 变大 \(1\) 变成 \(j+1\)，如果原先 \(j\) 已满足条件，旧新条件式分别为：

• \(c_{ls,j+1}-1+sum_{ls}-jp\ge c_{rs,k}\)

• \(c_{ls,j+2}-1+sum_{ls}-jp-p\ge c_{rs,k-1}\)

会发现左边变大，右边变小，所以上面满足下面一定也满足。

考虑此时两次对 \(c_{u,i}\) 的贡献，旧新分别是：

• \(c_{u,i}\overset{\underset{\min}{}}{\gets}\max\{c_{ls,j},c_{rs,k}-sum_{ls}+jp\}\)

• \(c_{u,i}\overset{\underset{\min}{}}{\gets}\max\{c_{ls,j+1},c_{rs,k-1}-sum_{ls}+jp+p\}\)

会发现 \(c_{ls,j+1}>c_{ls,j}\) 且转移条件 \(c_{ls,j+1}-1+sum_{ls}-jp\ge c_{rs,k}\) 得 \(c_{ls,j+1}\ge c_{rs,k}+1-sum_{ls}+jp\)。

所以第二次的贡献中 \(c_{ls,j+1}\) 已经大过第一次贡献的两项，说明第二次贡献不优。

所以 \(j\) 越小越好！！那么从大到小枚举 \(i\)，则 \(j\) 就可以双指针维护了。

当然这里双指针还要证明 \(i\) 减 \(1\) 后原先 \(j\) 满足条件。这是显然的，会发现条件中只有右边 \(c_{rs,k}\) 变成 \(c_{rs,k-1}\)。

这样 push_up 复杂度 \(\Theta(len)\)，总复杂度 \(\Theta(n\log n+m\log^2n)\)。

part5