暑假(3)
NOIP2023模拟测试赛(十六)
A
手玩一下可以发现,\(i\) 向 \(a_i\) 连边得到若干环,\(k\) 次操作内一定可以得到任意环数 \(\in[n-k,n]\) 的方案。
现在即对于每个 \(i\in[0,k]\),求把 \(n\) 个不同的数放进 \(n-i\) 个相同的环的方案数。
这个即 \(n\brack{n-i}\)。但是 \(n\) 很大,不能直接求。
考虑,这些环很多大小都是 \(1\)。枚举环大小不为 \(1\) 的环数量,考虑求:
- \(f_{n,m}\) 表示 \(n\) 个不同的数放入 \(m\) 个环中,每个环大小 \(\ge2\) 的方案数。
这个可以递推,具体地:
\[f_{n,m}=(n-1)f_{n-2,m-1}+(n-1)f_{n-1,m} \]前面的表示第 \(n\) 个数与前面某一个数放到新的环中,方案数是选择这个数的方案乘上 \(f_{n-2,m-1}\)。
后面表示这个数放在已有环里。方案数是放的位置方案乘上 \(f_{n-1,m}\)。
最终答案即 \(\displaystyle\sum_{i=0}^k\sum_{j=1}^{\min(i,n-i)}\binom{n}{i+j}f_{i+j,j}\)。
组合数头上很大。要预处理。复杂度 \(\mathcal O(k^2)\)。
B
经典反悔贪心,求 \(k\) 次最大子段和,每次把最大子段取反。线段树,复杂度线性对数。
C
没有 \(0\),因此段长越大整个数一定越大。
那么答案长度一定是 \(\lceil\frac nk\rceil\)。而且,除了 \(\lceil\frac nk\rceil\) 的段,一定存在一种答案划分,其余段长为 \(\lceil\frac nk\rceil-1\)。
证明,设 \(len=\lceil\frac nk\rceil\)。则假设答案中长度为 \(len\) 的段将环劈成几段。
在两段长为 \(len\) 的段中间的空隙中,我们可以将若干个数合并为长为 \(len-1\) 的段。
剩下一些不足 \(len-1\) 的段,可以与下一个长为 \(len\) 的段重新划分,这样一定更优。
一直重复这个过程,就只存在长度为 \(len\) 和 \(len-1\) 的段了。
现在考虑二分答案。将 \(n\) 种不同的长为 \(len\) 的段拉出来排序,二分。
假设从小到大排序,二分到了排名为 \(x\) 的段。现在不能使答案中长为 \(len\) 的段出现排名大于 \(x\) 的。
考虑从某个位置 \(s\) 开始铺,如果当前向后 \(len\) 格的段能使用就匹配 \(len\) 的段,否则匹配 \(len-1\) 的段。
这样 \(k\) 次看是否能走回起点 \(s\)。如果能则这个 \(x\) 是合法的。
\(s\) 实际上只需要取 \(len\) 种。这样可以覆盖所有情况。
至于如何排序 \(n\) 个段,可以直接后缀排序,求这个后缀的排名。
就算后缀排序认为两个段不同,但实际上它们只截 \(len\) 的长度是相同的,也不影响,因为换过来还会算一遍。
每次二分 check 是 \(\mathcal O(len\times k)\) 的,即 \(\mathcal O(n)\)。
复杂度 \(\mathcal O(n\log n)\)。
NOIP2023模拟测试赛(十七)
A
显然 \(f_0(n)=2^{\omega(n)}\),\(\omega(n)\) 表示 \(n\) 的不同质因子个数。
又 \(f_r(n)=\sum_{d|n}f_{r-1}(d)\),因此 \(f\) 都是积性函数。
考虑把 \(n\) 质因数分解,求出若干 \(f_r(p^k)\) 然后乘起来。
现在就是要求 \(f_r(p^k)\)。注意到 \(f_r(p^k)=\sum_{i=0}^kf_{r-1}(p^i)\),且 \(f_0(1)=1,f_0(p^k)=2\)。
那么可以发现实际上 \(f_r(p^k)\) 就是对数组 \(\{1,2,2,2,2,\dots\}\) 做 \(r\) 次前缀和,求 \(k\) 列的值。
这个组合数推一推就好了。复杂度 \(\mathcal O(q\frac{\sqrt n}{\log n})\)。
B
首先,假设每天都在吃东西,我们将一些天转化为睡觉,要满足:
- 连续 \(k\) 天中睡觉天数在 \([m_s,k-m_e]\) 内。
某天睡觉的权值是 \(s_i-e_i\)。即求满足条件下权值最大值,最后在加上所有 \(e\) 之和。
设 \(L=m_s,R=k-m_e\)。考虑建模:
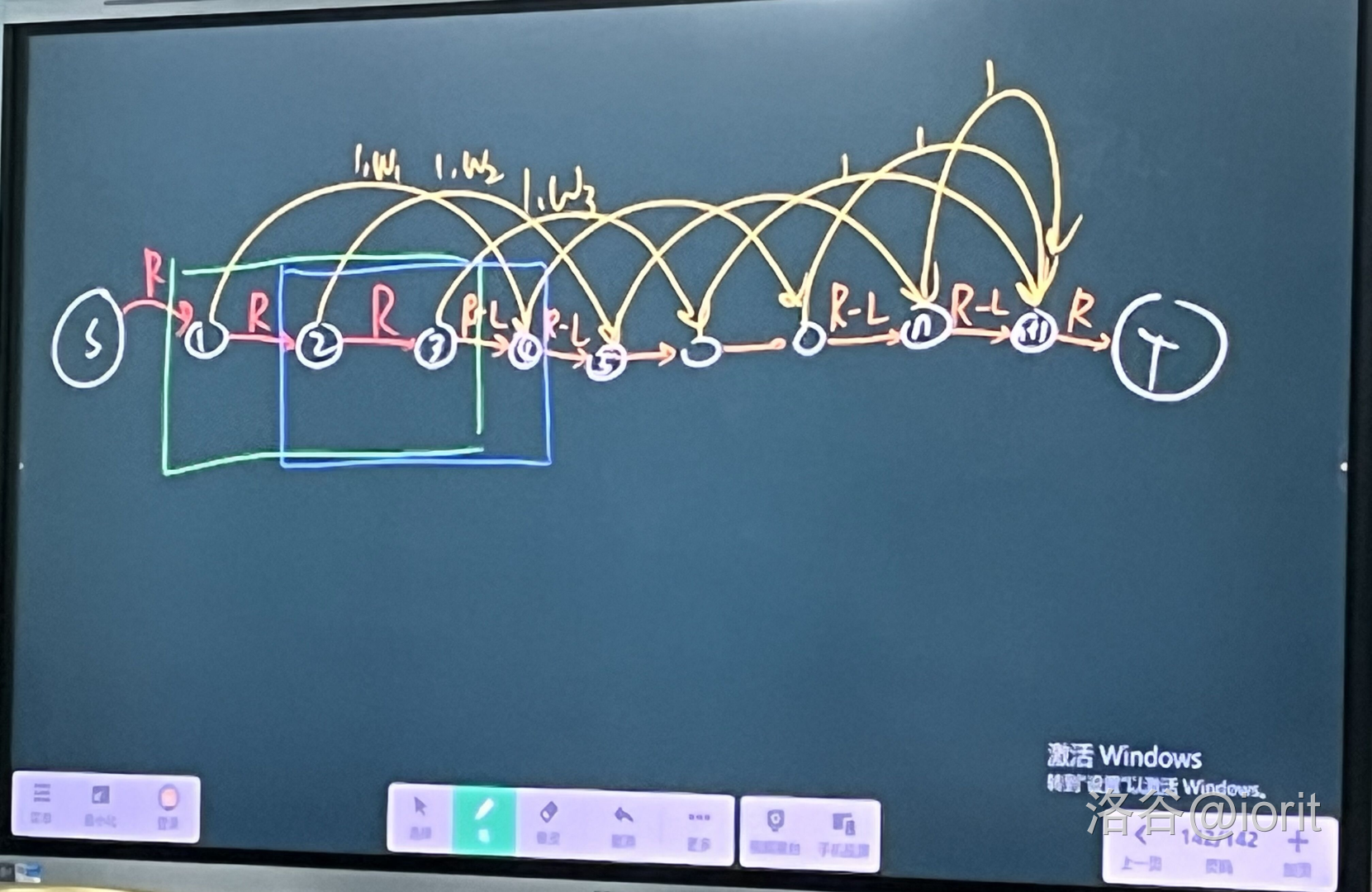
上图中,假设 \(k=3\)。
-
源点连 \(1\),流量 \(R\) 费用 \(0\)。
-
对于 \(i<k\),\(i\) 连 \(i+1\),流量 \(R\) 费用 \(0\)。
-
对于 \(k\le i\le n\),\(i\) 连 \(i+1\),流量 \(R-L\) 费用 \(0\)。
-
对于 \(1\le i\le n\),\(i\) 连 \(\min(i+k,n)\),流量 \(1\) 费用 \(e_i-s_i\)。
-
\(n+1\) 连汇点,流量 \(R\) 费用 \(0\)。
求最大费用最大流即为答案。
为什么?这里如果 \(i\) 连 \(\min(i+k,n)\) 有流量就表示选了点 \(i\) 睡觉。
首先发现最大流一定是 \(R\)。最大流不会大于 \(R\),因为每条边流量最大就是 \(R\);
而且可以找到最大流为 \(R\) 的方案。具体地:
-
从下面的主干走可以流走 \(R-L\) 的流量。
-
对于所有的 \(1\le i\le k\) ,有一条路径 \(i\to i+k\to i+2k\to\cdots\to n+1\)。
由于前 \(k\) 条主干边流量为 \(R\),且 \(L\le k\),这 \(k\) 条路径一定能流出 \(L\) 的流量。
所以总流量就是 \(R-L+L=R\)。因此最大流等于 \(R\)。
现在考察每一个长度为 \(k\) 的区间,如上图中的绿框或者蓝框,要证明黄边流出的流量和在 \([L,R]\) 内。
\(\le R\) 是显然的,否则总流量大于 \(R\)。
我们可以归纳证明,每个这样的区间流入流量与流出流量都等于 \(R\)。
具体地,例如会发现,绿框比蓝框多出来的部分流量也流进了蓝框。
为什么黄边流出总流量 \(\ge L\)?由于总流出流量为 \(R\),主干边最多流出 \(R-L\),那么黄边最少流出 \(L\)。
这样就保证了题目的所有限制。
复杂度可能是 \(\mathcal O(nk)\) 吗?
C
对所有 \(S\) 建立 ACAM,设为 \(A1\);对反串再建一个 ACAM,设为 \(A2\)。
考虑求出有多少组 \(i,j\),其中 \(i\) 是串 \(T\) 中的下标,\(j\) 是某个 \(S_k\) 中的下标,满足:
-
\(S_{k,[1,j-1]}\) 与 \(T_{[i-(j-1),i-1]}\) 匹配。
-
\(S_{k,[j+1,m]}\) 与 \(T_{[i+1,i+(m-j)]}\) 匹配,\(m=|S_k|\)。
如果匹配成功,表示可以修改 \(T_i\) 来匹配。
这样会导致一些算重,具体地,如果这位修改成原来的值,会和不修改时的匹配数算重。这些很好处理。
现在就是要求有多少对这样的 \(i,j\)。
假设 \(S_k\) 的前缀 \(j-1\) 在 \(A1\) 中的点是 \(x\),后缀 \(j+1\) 在 \(A2\) 中的点是 \(y\),
\(T\) 的前缀 \(i-1\) 在 \(A1\) 中走到了 \(u\),后缀 \(i+1\) 在 \(A2\) 中走到了 \(v\)。
那么满足两个匹配当且仅当,\(u\) 在 \(A1\) 的 fail 树上在 \(x\) 的子树内,\(v\) 在 \(A2\) 的 fail 树上在 \(y\) 的子树内。
转换到序列上,就是 \(dfn_u\) 要在一个区间内,\(dfn_v\) 要在一个区间内。
枚举 \(j\) 的话,每次就是一个二维数点。复杂度 \(\mathcal O(n\log n)\)。
NOIP2023模拟测试赛(十八)
A
设 \(dp_{i,j}\) 表示删到只剩下 \([i,j]\) 所需最小船数,同时记录这个前提下最后一艘船已装的重量最小值。
转移直接从 \(dp_{i+1,j}\) 和 \(dp_{i,j+1}\) 转移。空间可能开不下,可以滚掉一维。
复杂度平方。
B
考虑枚举每个值 \(x\),设 \(x\) 为区间最大值,考虑所有 \(=x\) 的位置拉出来,假设第 \(i\) 个等于 \(x\) 的位置是 \(pos_i\)。
二分出 \(pre_i,nxt_i\) 分别表示 \(pos_i\) 前/后第一个 \(\ge x\) 的位置。
对每一段满足相邻 \(pos\) 间有 \(nxt_i=pos_{i+1}\) 的段分别处理。即,相邻的 \(x\) 间没有比 \(x\) 大的。
处理出这些 \(x\) 将序列分成了若干段,每段长度为 \(len_i\)。
假设这一段有 \(k\) 个点,我们得到 \(len_0\sim len_{k}\)。
(\(len_i\) 表示 \(i\) 到下一个点的长度,第 \(0\) 段从 \(pre\) 开始,最后一段到 \(nxt\))
那么最大值有 \(1\) 个的区间数即 \(len_0len_1+len_1len_2+\cdots len_{k-1}len_k\)。
有 \(d\) 个,即 \(\sum_{i-j=d}len_{i}len_{j}\)。显然是一个差卷积的形式,FFT 即可。
复杂度线性对数。
C
涉及中位数有一个 trick:检验一个数能否是中位数,只需将大于它的数设为 \(1\),小于的数设为 \(-1\),求最大权值的连通块是否 \(>0\) 即可。
这题如果检验是否能是 \(a-\) 中位数,只需看最大权值连通块是否 \(>a\)。
按权值从大到小排序,对于当前的数,将大于它的设为 \(1\),小于设为 \(-1\),求树上最大连通块。
这个可以树形 \(dp\),设 \(f_u\) 表示 \(u\) 为根的子树,选了 \(u\) 的最大权值连通块。
则 \(f_u=w_u+\max\{f_{ls},0\}+\max\{f_{rs},0\}\)。
注意到从大到小排序,每次只会修改当前点的 \(1/-1\) 权值。
这样只会涉及到根路径上 \(f\) 的变化,\(\mathcal O(\log n)\) 暴力修改即可。
复杂度线性对数。