0.前言
又称淀粉质。
学科营之前赶紧来一波急抓。
1.引入
我们考虑这样一个问题,对于一棵树,我们求出树上所有路径长度小于等于 \(k\) 的路径总数。
首先不难想到一种 \(n^3\) 的暴力做法,即枚举两个端点,然后暴力出路径。
考虑找路径的时候优化一下,采用倍增或者树链剖分将复杂度变为 \(n^2 \log n\)。
还可以优化一下:将每个节点当做一个根节点,每次 \(dfs\) 一下,当搜索的距离比限制要大的时候就退出。时间复杂度 \(O(ans)\),最慢卡到 \(n^2\)。
但显然,这些还是不够优秀。
2.具体做法
我们可以考虑随便指定一个根节点 \(p\),
则我们可以考虑把树上的路径分为两类:
-
经过根节点 \(p\) 的路径。
-
路径全部在 \(p\) 的子树下面。
显然,对于第二种路径,既然算法叫点分治,我们可以考虑对他的子树进行递归处理。换句话说,就是我们只需要对于每个根节点 \(p\) 只需要求出经过他的路径的长度不超过 \(k\) 的总数。
可以考虑将这样的路径分为两度,假设该路径的左右端点分别为 \(x,y\)。则我们可以将路径分成两段:\(x-p\) 和 \(p-y\)。然后我们在分别维护两个数组:\(d,b\)。其中, \(d_i\) 表示 \(i\) 到根节点的距离,\(b_i\) 表示 \(i\) 属于根节点下的哪一棵子树。
例如,对于下面的一棵树:
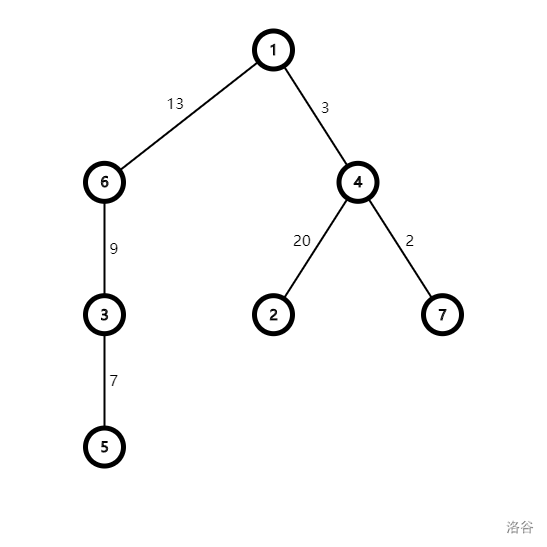
\(d_1=0,d_2=23,d_3=22,d_4=3,d_5=29,d_6=13,d_7=5\)。
\(b_2=4,b_3=6,b_4=4,b_5=6,b_6=6,b_7=4\)。
特别的,令 \(b_1=1\)。
此时,满足限制的第一种路径就一定满足一下两个条件:
-
\(b_x \not= b_y\)
-
\(d_x+d_y \le k\)。
我们定义函数 \(calc(p)\) 表示对于以 \(p\) 为根节点的第一种路径的个数,我们的目标就是实现这个 \(calc(p)\) 的计算。
我们考虑再维护一个数组 \(a\),用于储存树中的每一个节点,并对里面的元素按照 \(d\) 数组的大小从小到大排序。
接着使用两个指针 \(l,r\) 分别从头和末尾扫描 \(a\) 数组。可以发现,对于满足 \(d_{a_l}+d_{a_r} \le k\) 在 \(l\) 递增的情况下,满足 \(r\) 递减,从而可以保证一个扫描时 \(O(n)\) 的复杂度。
对于答案的统计,考虑再维护一个桶 \(cnt_i\),表示在 \([L+1,r]\) 中 \(b_{a_x}=i\) 的个数。所以,对于每对满足 \(d_{a_l}+d_{a_r} \le k\) 的 \((l,r)\),都有对于答案 \(r-l-cnt_{b_{a_l}}\) 的贡献。
然后求完 \(calc(p)\) 之后,我们就可以对他的子树进行递归了求解了。
3.时间复杂度及优化
可以发现,对于上述算法,假设递归层数为 \(T\),则由于我们每递归一层,就会处理一个 \(O(n)\) 量级的操作,再加上求 \(calc(p)\) 的时间瓶颈排序的 \(n \log n\),总时间复杂度为 \(Tn\log n\)。
显然,我们很容易就可以将算法卡到 \(n^2\log n\) 去,这甚至不优于我们一开始的算法,显然不是我们想要的结果。
仔细观察算法可以发现,当我们每次递归子树的时候,我们选取里面的任意一个点作为这个子树的根节点都不会对答案造成影响,也就是说,我们可以通过选取子树中不同的节点作为根节点来优化递归层数。
再迁移到我们以前学过的一些东西,于是,我们想到了树的重心。我们可以考虑每次选取每个树的重心作为根节点进行递归。
这个时候,我们再来思考一下复杂度。我们知道,当我们删除一个重心时,每个子树的大小不会超过总子树的一半,所以在递归时,层数就不可能超过 \(\log n\),所以总时间复杂度就为 \(n \log ^2n\)。
代码
数组开的太多了,清空数组写的很丑,调了半天,不要学习。
#include<bits/stdc++.h>
using namespace std;
int n,k;
struct node
{
int tar,num,nxt;
}arr[80005];
int fst[40005],cnt;
void adds(int x,int y,int z)
{
arr[++cnt].tar=y,arr[cnt].nxt=fst[x],fst[x]=cnt,arr[cnt].num=z;
}
int d[40005],b[40005],size[40005],s[40005];
int a[40005],tot,nn,cn[40005];//注意这个nn,每次求中心的时候,记得改变整棵树的大小!
bool cmp(int x,int y)
{
return d[x]<d[y];
}
bool vis[40005];
vector<int> used,used2;
int anss=INT_MAX,pos;
void init()//求重心的一个初始化,开used防止memset爆掉
{
for(int i=0;i<used.size();++i)
d[used[i]]=0,size[used[i]]=0;
used.clear();
anss=INT_MAX,pos=0;
}
void heavy(int x,int last)//求重心
{
int max_part=0;
used.push_back(x);
size[x]++;
for(int i=fst[x];i;i=arr[i].nxt)
{
int j=arr[i].tar;
if(j==last||vis[j]) continue;
heavy(j,x);
size[x]+=size[j];
max_part=max(max_part,size[j]);
}
max_part=max(max_part,nn-size[x]);
if(max_part<anss)
{
anss=max_part;
pos=x;
}
}
void dfs(int x,int last,int num)
{
//对于每棵树求a,b,d
used2.push_back(x);
a[++tot]=x;
s[x]++;
if(num) b[x]=num;
for(int i=fst[x];i;i=arr[i].nxt)
{
int j=arr[i].tar;
if(j==last||vis[j]) continue;
d[j]=d[x]+arr[i].num;
if(num) dfs(j,x,num);
else dfs(j,x,j);
s[x]+=s[j];
}
}
int calc(int x)
{
vis[x]=true;
d[x]=0,tot=0;
for(int i=0;i<used2.size();++i) b[used2[i]]=s[used2[i]]=0;
used2.clear();
dfs(x,0,0);
//以上又是神级超丑初始化
stable_sort(a+1,a+tot+1,cmp);
int L=1,R=tot;
for(int i=1;i<=tot;++i) cn[b[a[i]]]++;
int ans=0;
for(;L<=R;++L)
{
cn[b[a[L]]]--;
while(k-d[a[R]]<d[a[L]]&&R>=L) cn[b[a[R]]]--,R--;
if(R<L) break;
ans+=R-L-cn[b[a[L]]];
}
//以上是指针扫描
for(int i=1;i<=tot;++i) cn[b[a[i]]]=0;//记得手动改还原,不要memset!
vector<int> p;
for(int i=fst[x];i;i=arr[i].nxt) if(!vis[arr[i].tar]) p.push_back(s[arr[i].tar]);//s可能后面会被改变,所以先存下来。
int bj=0;
for(int i=fst[x];i;i=arr[i].nxt)
{
int j=arr[i].tar;
if(vis[j]) continue;
init();
nn=p[bj++];
heavy(j,0);
ans+=calc(pos);//递归
}
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;++i)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
adds(u,v,w);
adds(v,u,w);
}
cin>>k;
nn=n;
heavy(1,0);
cout<<calc(pos)<<endl;
return 0;
}
4.例题
即上述题目。
其实没有什么大的差别,只需要改变指针扫描这一块,直接上 \(calc\) 函数的代码。
void calc(int x)
{
vis[x]=true;
d[x]=0,tot=0;
for(int i=0;i<used2.size();++i) b[used2[i]]=s[used2[i]]=0;
used2.clear();
dfs(x,0,0);
bool ans=0;
sort(a+1,a+tot+1,cmp);
for(int qwq=1;qwq<=k;++qwq)
{
if(answer[qwq]) continue;
int kk=dis[qwq];
int L=1,R=tot;
while(L<=R)
{
if(d[a[L]]+d[a[R]]>kk) R--;
else if(d[a[L]]+d[a[R]]<kk) L++;
else if(b[a[L]]==b[a[R]])
{
if(d[a[R]]==d[a[R-1]]) R--;
else L++;
}
else
{
answer[qwq]=true;
break;
}
}
}
vector<int> p;
for(int i=fst[x];i;i=arr[i].nxt) if(!vis[arr[i].tar]) p.push_back(s[arr[i].tar]);
int bj=0;
for(int i=fst[x];i;i=arr[i].nxt)
{
int j=arr[i].tar;
if(vis[j]) continue;
init();
nn=p[bj++];
heavy(j,0);
calc(pos);
}
}
这里注意一个细节:记得把询问提到递归函数里面,而不是在外面限定路径长度,也是一个玄学常数优化,不然会 T 飞。具体可以看这个帖子。
就是第二个问题的升级版。可以考虑再维护一个数组 \(dep\) 用来记录当前子树下每个点的深度,在统计答案的时候变成 \(ans=d_{a_l}+d_{a_r}\) 并且记得不要跳出循环即可。
关键 \(calc(p)\) 代码:
int calc(int x)
{
vis[x]=true;
d[x]=dep[x]=0,tot=0;
for(int i=0;i<used2.size();++i) b[used2[i]]=s[used2[i]]=0;
used2.clear();
dfs(x,0,0);
sort(a+1,a+tot+1,cmp);
int kk=k;
int L=1,R=tot;
int ans=INT_MAX;
while(L<=R)
{
if(d[a[L]]+d[a[R]]>kk) R--;
else if(d[a[L]]+d[a[R]]<kk) L++;
else if(b[a[L]]==b[a[R]])
{
if(d[a[R]]==d[a[R-1]]) R--;
else L++;
}
else
{
ans=min(ans,dep[a[L]]+dep[a[R]]);
if(d[a[R]]==d[a[R-1]]) R--;
else L++;
}
}
vector<int> p;
for(int i=fst[x];i;i=arr[i].nxt) if(!vis[arr[i].tar]) p.push_back(s[arr[i].tar]);
int bj=0;
for(int i=fst[x];i;i=arr[i].nxt)
{
int j=arr[i].tar;
if(vis[j]) continue;
init();
nn=p[bj++];
heavy(j,0);
ans=min(ans,calc(pos));
}
return ans;
}
5.后记
其实点分治的题目解法还是大同小异的,除了有些特别变态的题目,主要还是觉得就有亿点难调。(不知道为什么我打出来的数组就这么多,清空数组反倒成为了我的难题。)
标签:arr,路径,tar,int,分治,笔记,学习,calc,节点 From: https://www.cnblogs.com/SFsaltyfish/p/18049149