基础线段树笔记

作为学会的第一个高级数据结构，当然要提早记录啦（虽然好像已经拖了一学期了）

线段树的主要用途是针对一些较复杂的区间问题，如：

给你一个长度为 \(n\) 的序列，还有 \(m\) 次操作。
对于每次操作，让你将一个位置 \(x\) 加 \(y\),或查询区间 \(\left[L, R\right]\) 的和。

首先，如果只要求查询，那么只要求前缀和即可。
但是此题还有区间的修改操作，这时就要用到线段树了。

线段树的原理：

线段树，顾名思义，就是一棵树，但上面的节点变成了一个个区间。

线段树一般采用二叉树的形式。
对于每个节点，我们要维护四个信息：节点的编号，节点所对应的区间左右端点和所求的值。

一般线段树长这个样子（图丑勿喷）：

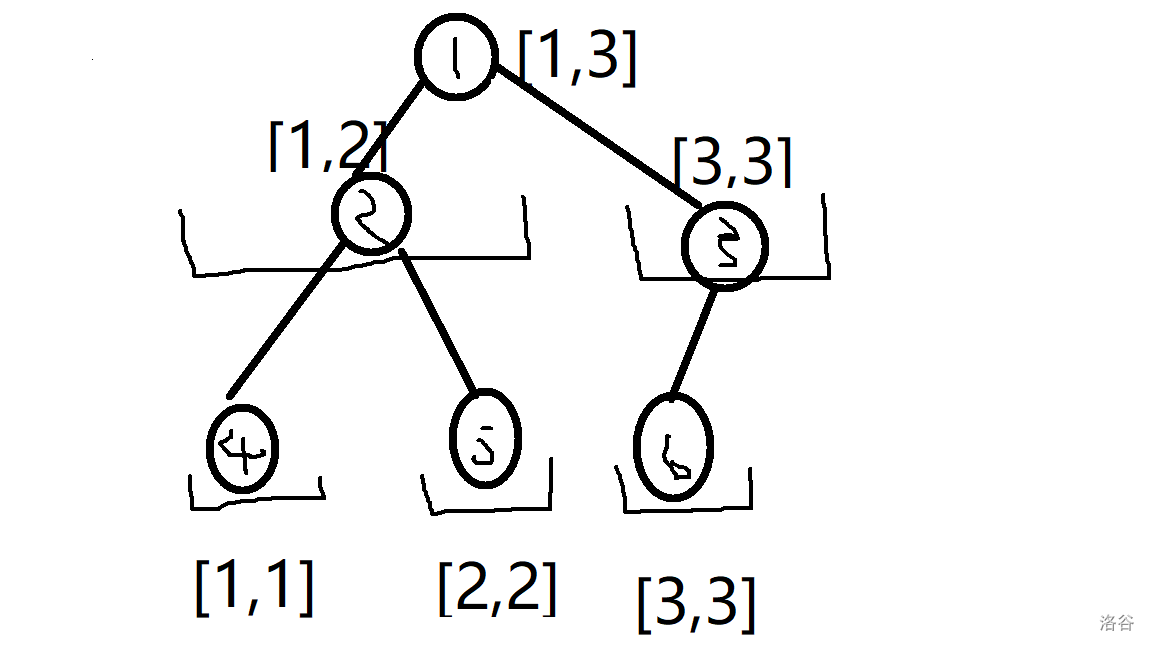
而线段树的高效正是因为这些线段。

建立线段树：

想要使用线段树，肯定要先建立一颗线段树。
由于线段树基于二叉树，那么我们可以以下标为编号，且一个节点 \(x\) 的左节点为 \(2x\)，右节点为 \(2x+1\)。

观察上图，我们可以发现，一个节点的左儿子区间为大区间的前半部分，右儿子为后半部分。
因二叉树有很明显的拓扑序，所以我们可以用递归构造这么一棵树，在回溯时自向上合并信息。

code:

void biuld(int u, int l, int r) { //  建树
  if (l == r) {  //  特判叶子节点
    w[u] = a[l];
    return;
  }
  int mid = l + r >> 1;
  biuld(u << 1, l, mid); // 递归建造前半部分
  biuld(u << 1 | 1, mid + 1, r);   // 递归建造后半部分
  w[u] = w[u << 1] + w[u << 1 | 1]; // 合并子节点
}

注：代码中合并子节点的部分如果合并过程比较复杂，可以将其写成一个函数。

区间查询

现在我们已经得到了一颗线段树，所以我们可以对其进行操作了。
对于求一个区间的和 \(\left[L, R\right]\)，我们可以将其分为几个子区间，然后递归求解每一个部分。

这时问题就来了，我们该怎样去分解区间呢？

观察线段树，我们可以考虑把每个区间变为 \(\left[L, mid\right]\) 与 \(\left[mid+1, R\right]\) 两个区间（你没有看错，就跟 \(\operatorname{build}\) 函数一样）。
那么对于每个区间，我们只要递归下去就可以了。
可这样子到最后也是 \(\operatorname{O}(n)\) 的，这时我们就要考虑优化。

经过思考不难发现，我们当前到的每一个节点所对应的区间只会有三种：

1. 该区间与查询区间完全无关，如图（红色代表当前区间，黑色为查询区间）：
   

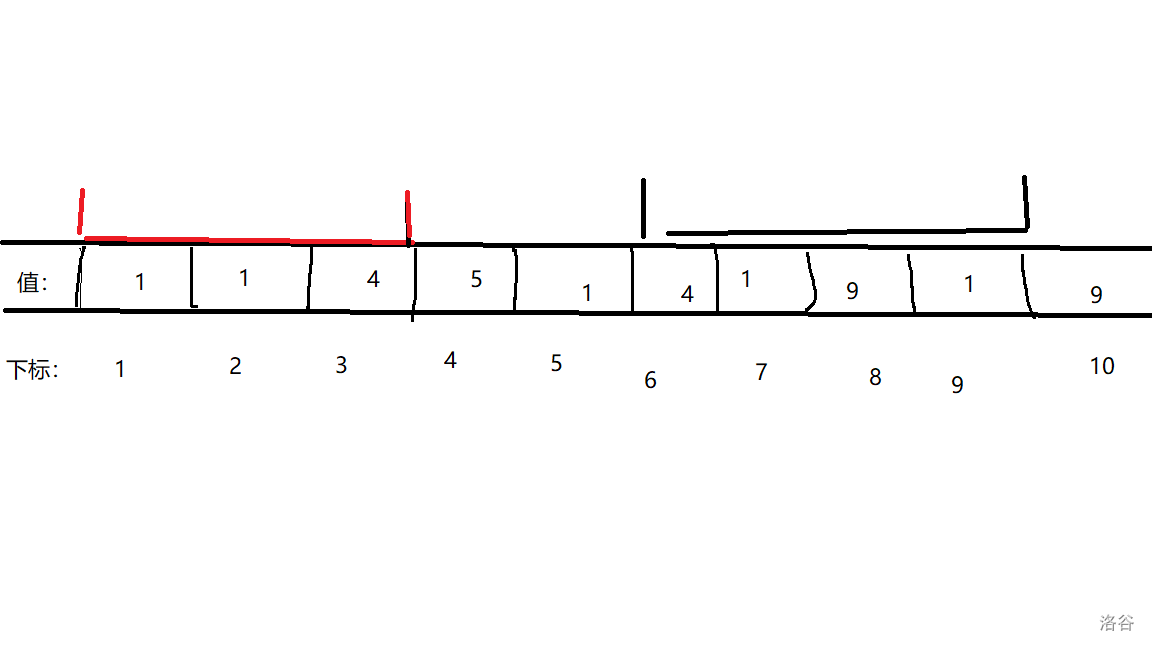
2. 该区间被查询区间完全包含，如图：
   

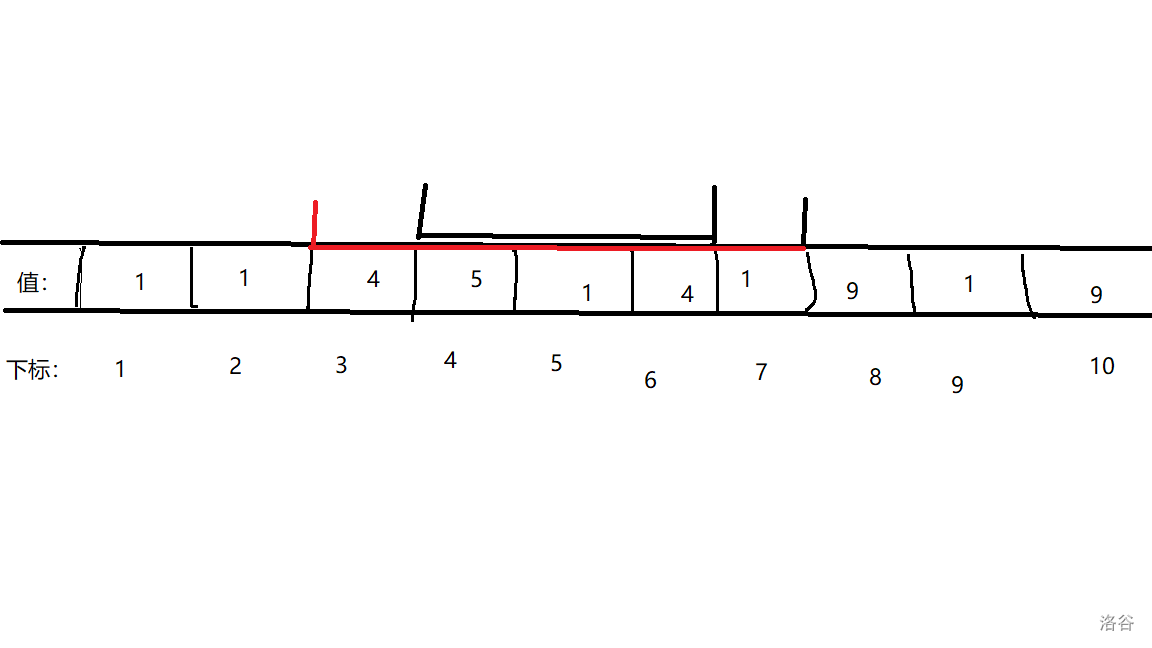
3. 该区间与查询区间有部分交集，如图：
   

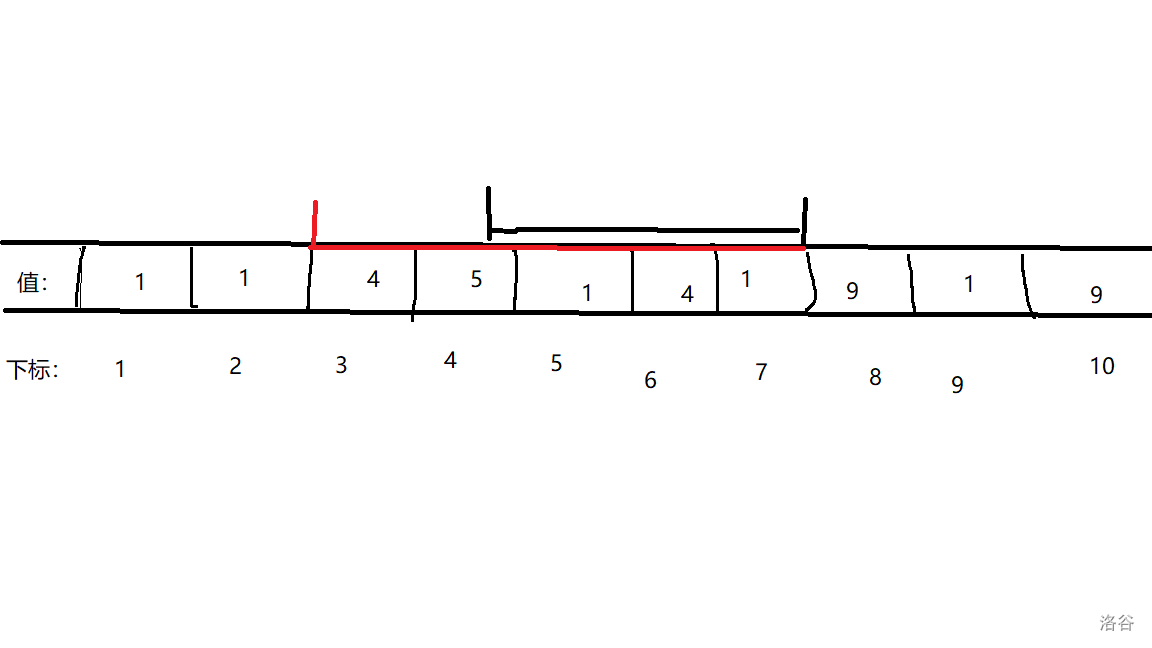
对于第 1 种情况，我们只需要返回一个及劣值即可（如区间和返回 0，区间最大值返回 \(-Inf\) ）。

对于情况 2，该区间已经被完全包含，返回当前所维护的信息即可。

对于第 3 种情况，我们考虑把区间分为两半，然后依次进行求解。

CODE:

int query(int u, int l, int r, int L, int R) {  //  查询
  if (l > R || r < L) {                         //  情况 1
    return 0;
  } else if (L <= l && r <= R) {  //  情况 2
    return w[u];
  } else {  //  情况 3（直接用else即可，因为其比较复杂）
    int mid = l + r >> 1;
    push_down(u, l, r);
    return query(u << 1, l, mid, L, R) + query(u << 1 | 1, mid + 1, r, L, R);
  }
}

区间修改

区间修改应该可以说是线段树中最复杂的了。

暴力修改叶子节点明显是不可行的，我们考虑更快的方法。

我们知道一个区间是由多个区间拼起来的。而大多数情况下区间都是完整的（如区间查询中的情况 2 ）。那么我们可以考虑给区间打上一个标记，等区间要被分裂的时候再修改，这个东西叫做 Lazy_tag。

和区间查询一样，区间修改时可以分为三种情况（可回去看区间查询的图）：

对于情况 1，我们直接结束递归即可。

对于情况 2，我们可以给当前区间打上标记。

对于情况 3，我们需要把当前区间所对应的节点上的标记下传给子节点，然后再递归处理两个子区间。

CODE:

void add_tag(int u, int l, int r, LL x) {  //  打标记
  w[u] += (r - l + 1) * x, tag[u] += x;
}

void push_down(int u, int l, int r) {  //  下传标记
  if (tag[u]) {                        //  有标记才下传
    int mid = l + r >> 1;
    add_tag(u << 1, l, mid, tag[u]);          //  给左儿子打标记
    add_tag(u << 1 | 1, mid + 1, r, tag[u]);  //  给右儿子打标记
    tag[u] = 0;
  }
}

void update(int u, int l, int r, int L, int R, LL x) {  //  修改
  if (L <= l && r <= R) {                               //  完全包含，直接打标记
    add_tag(u, l, r, x);
  } else if (l > R || r < L) {  //   没有相交部分，直接返回
    return;
  } else {
    int mid = l + r >> 1;
    push_down(u, l, r);                       //  先把标记下传
    update(u << 1, l, mid, L, R, x);          // 处理左区间
    update(u << 1 | 1, mid + 1, r, L, R, x);  // 处理右区间
    push_up(u);                               //  更新当前节点
  }
}

注：查询时也会分裂区间，所以也要下传标记

P3327完整代码如下：

#include <bits/stdc++.h>

using namespace std;
using LL = long long;

const int kMaxN = 2e5 + 5;

LL n, m, a[kMaxN], w[kMaxN << 2], tag[kMaxN << 2];

void push_up(int u) {
  w[u] = w[u << 1] + w[u << 1 | 1];
}

void biuld(int u, int l, int r) { //  建树
  if (l == r) {  //  特判叶子节点
    w[u] = a[l];
    return;
  }
  int mid = l + r >> 1;
  biuld(u << 1, l, mid); // 递归建造前半部分
  biuld(u << 1 | 1, mid + 1, r);   // 递归建造后半部分
  push_up(u); // 合并子节点
}

void add_tag(int u, int l, int r, LL x) {  //  打标记
  w[u] += (r - l + 1) * x, tag[u] += x;
}

void push_down(int u, int l, int r) {  //  下传标记
  if (tag[u]) {                        //  有标记才下传
    int mid = l + r >> 1;
    add_tag(u << 1, l, mid, tag[u]);          //  给左儿子打标记
    add_tag(u << 1 | 1, mid + 1, r, tag[u]);  //  给右儿子打标记
    tag[u] = 0;
  }
}

void update(int u, int l, int r, int L, int R, LL x) {  //  修改
  if (L <= l && r <= R) {                               //  完全包含，直接打标记
    add_tag(u, l, r, x);
  } else if (l > R || r < L) {  //   没有相交部分，直接返回
    return;
  } else {
    int mid = l + r >> 1;
    push_down(u, l, r);                       //  先把标记下传
    update(u << 1, l, mid, L, R, x);          // 处理左区间
    update(u << 1 | 1, mid + 1, r, L, R, x);  // 处理右区间
    push_up(u);                               //  更新当前节点
  }
}

int query(int u, int l, int r, int L, int R) {  //  查询
  if (l > R || r < L) {                         //  情况 1
    return 0;
  } else if (L <= l && r <= R) {  //  情况 2
    return w[u];
  } else {  //  情况 3（直接用else即可，因为其比较复杂）
    int mid = l + r >> 1;
    push_down(u, l, r); //  记得下传
    return query(u << 1, l, mid, L, R) + query(u << 1 | 1, mid + 1, r, L, R);
  }
}

int main() {
  cin >> n >> m;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  biuld(1, 1, n);
  for (LL x, y, k, op; m; m--) {
    cin >> op >> x >> y;
    if (op == 1) {
      cin >> k;
      update(1, 1, n, x, y, k);
    } else {
      cout << query(1, 1, n, x, y) << "\n";
    }
  }
  return 0;
}