题单:
题解有时间就写,一般会咕。
P5691 [NOI2001] 方程的解数
简单的折半搜索。
直接搜索时间复杂度是 \(O(m^6)-O(m^6\log p_i)\) 的(快速幂),无法通过。
考虑优化,首先我们对上面的式子做一个变形:
\[\sum_{i=1}^{n}k_ix_i^{p_i}=0 \]即
\[\sum_{i=1}^{\lfloor\frac{n}{2}\rfloor}k_ix_i^{p_i}+\sum_{i=\lfloor\frac{n}{2}\rfloor}^{n}k_ix_i^{p_i}=0 \]即
\[-\sum_{i=1}^{\lfloor\frac{n}{2}\rfloor}k_ix_i^{p_i}=\sum_{i=\lfloor\frac{n}{2}\rfloor}^{n}k_ix_i^{p_i} \]那么我们只需要对 \([1,\lfloor\frac{n}{2}\rfloor]\) 和 \([\lfloor\frac{n}{2}\rfloor+1,n]\) 两段分别进行搜索即可。考虑到每种方案所选的未知数都不同,所以搜出几个数就存在几种方案。
时间复杂度 \(O(m^3\log p_i)\),可以通过。
优化:此题不卡模数,将 map 更换为 unordered_map 并预处理幂次就可以去掉那一只 \(\log\)。
代码(不带优化):
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
typedef long long ll;
//typedef __int128 lll;
typedef unsigned long long ull;
const int N=15;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,m,k[N],p[N],ans;
unordered_map<int,int>mp;
inline int power(int a,int b){
int res=1;
while(b){
if(b&1)res*=a;
a*=a,b>>=1;
}
return res;
}
void dfs1(int x,int sum){
// 1 to [n/2]
if(x>n/2){
mp[sum]++;
return;
}
for(int i=1;i<=m;++i) dfs1(x+1,sum+k[x]*power(i,p[x]));
}
void dfs2(int x,int sum){
// [n/2+1] to n
if(x>n){
ans+=mp[-sum];
return;
}
for(int i=1;i<=m;++i) dfs2(x+1,sum+k[x]*power(i,p[x]));
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;++i) k[i]=read(),p[i]=read();
dfs1(1,0);
dfs2(n/2+1,0);
println(ans);
return 0;
}
P1763 埃及分数
P1379 八数码难题
one - 模拟赛 D1T1
two - 模拟赛 D1T2
three - 模拟赛 D1T3
four - 模拟赛 D1T4
P3195 [HNOI2008]玩具装箱
很好的一道题。
首先考虑暴力 dp。
设:\(dp_i\) 表示考虑前 \(i\) 个元素所能获得的最小费用。
转移:考虑枚举 \(i\) 上一个区间的右端点,得
\[dp_i=\min_{j=0}^{i-1}dp_j+(i-j-1+\sum_{k=j+1}^{i}a_k-L)^2 \]注:这里用 \(a\) 数组来代替原题中的 \(c\) 数组。
这样朴素实现是 \(O(n^3)\) 的,使用前缀和优化即可做到 \(O(n^2)\),可以获得 \(70\) 分。
考虑优化,首先我们来推一下式子:
\[dp_i=\min_{j=0}^{i-1}dp_j+(i-j-1+\sum_{k=j+1}^{i}a_k-L)^2 \]记 \(sum_i=\sum_{j=1}^{i}a_j\),得:
\[dp_i=\min_{j=0}^{i-1}dp_j+(i-j-1+sum_i-sum_j-L)^2 \]实际算的时候这样就可以了,但是为了发掘更多的性质,我们还要继续推:
记 \(q_i=sum_i+i\),得:
\[dp_i=\min_{j=0}^{i-1}dp_j+[q_i-q_j-(L+1)]^2 \]展开,得:
\[dp_i=\min_{j=0}^{i-1}dp_j+q_i^2-2q_iL-2q_i+(L+1)^2-2q_iq_j+q_j^2+2q_jL+2q_j \]容易发现前面的一大堆都与 \(j\) 无关,我们令 \(K=q_i^2-2q_iL-2q_i+(L+1)^2\),然后提出来:
\[dp_i=K+\min_{j=0}^{i-1}dp_j-2q_iq_j+q_j^2+2q_jL+2q_j \]令 \(k_j=-2q_j,x=q_i-L-1,b_j=dp_j+q_j^2\),得:
\[dp_i=K+\min_{j=0}^{i-1}k_jx+b_j \]类似的,这个式子还可以转换为斜率优化的标准形式,然后维护凸包之类的东西。但是由于我不会斜率优化,这里就先不讲了。/kk
观察上面的式子,首先 \(K\) 是统一加上的,不用管,而剩下的就是 \(y=kx+b\) 的标准一元一次函数形式。
容易发现其实我们要求的是 \(y\),所以实际上就是求 \(x=q_i-L-1\) 这条线与若干条(实际上有 \(i\) 条)形如 \(y=k_jx+b_j\) 的直线的交点的纵坐标最小值。
然后我们就可以直接维护半平面交了。但是我还是不会,所以不会讲。
继续观察式子:由于 \(a_i\) 和 \(i\) 都大于 \(0\),所以 \(q_i\) 单调递增。再代入原式,得 \(k_j<0\) 且 \(k_j\) 单调递减,\(x\) 递增。
\(k_j<0\) 且单调递减带来一个很好的性质是,编号更大的直线一定比更小的直线斜率更大。
由于我们并不想求凸包或者半平面交,因此我们考虑使用二分栈。
记 \(z_i\) 表示 \(dp_i\) 的最优转移点,那么有一个很重要的性质:\(z_i\) 单调不降。
考虑证明,我们使用 GeoGebra 画图:
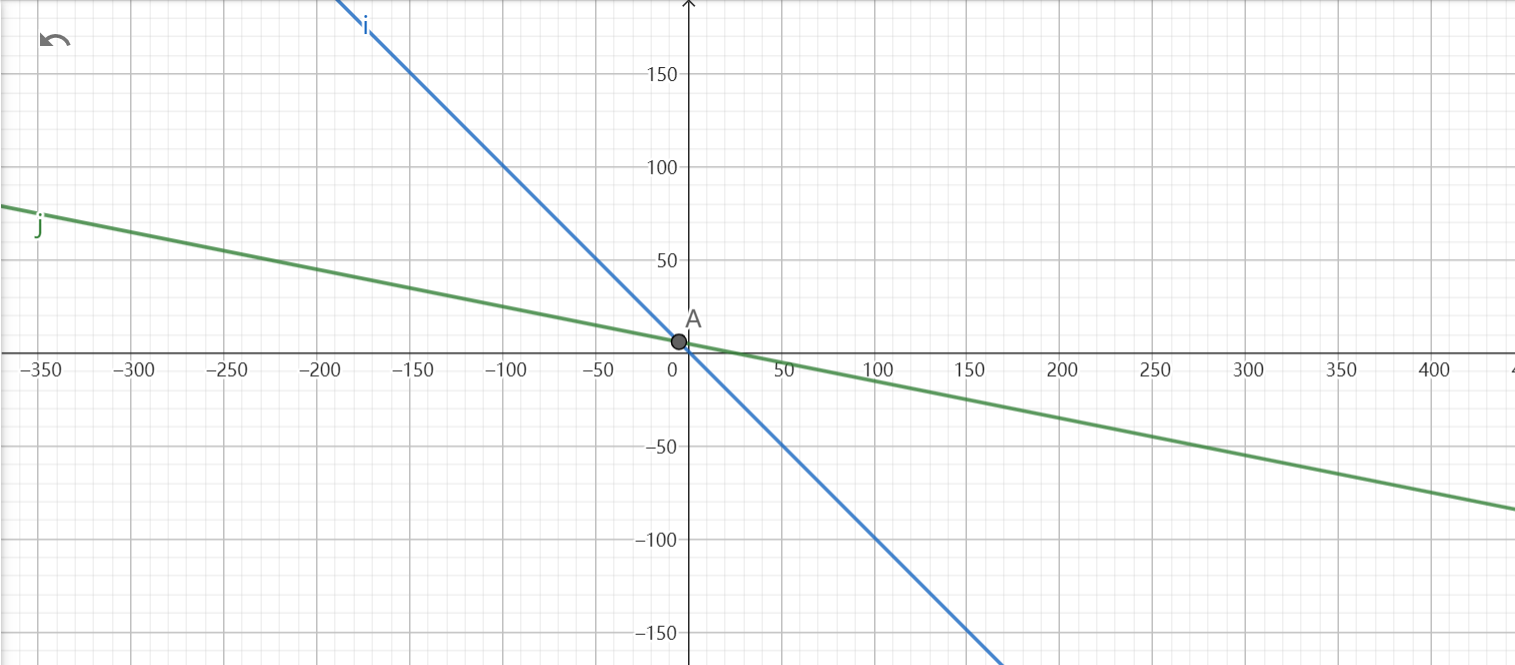
(其实我不太会用这个东西)
如图,蓝线为 \(i\),绿线为 \(j\)(编号),交点为 \(A\),且 \(j<i\)。
由于我们要求的是纵坐标最小值,那么容易发现横坐标在 \(A\) 左边时 \(j\) 更优,而在右边时 \(i\) 更优。由于横坐标 \(x=q_i-L-1\) 递增,所以 \(A\) 左侧的编号也必然小于其右侧的编号,也就证明了 \(z\) 单调不降。
这个时候我们发现 \(z\) 满足单调性,自然就可以二分了。
初始默认最优转移点 \(z=0\),然后就可以发现,每算出一个 \(dp_i\),就会更新 \(z\) 的一段后缀(单调不降)。因此我们可以用一个栈来维护这些最优转移点所管辖的区间。
具体地,在计算 \(dp_i\) 时,首先将栈内所有 \(r<i\) 的最优转移点弹出,因为它们已经失去了价值。其实只需要弹出一次,因为更前面的决策点已经被 \([1,i-1]\) 中的点弹出了。此时再用栈顶的最优决策点来更新 \(dp_i\) 的值。
现在我们需要用 \(dp_i\) 来更新最优决策点。由于是后缀,所以我们从栈底开始,暴力删除更劣的决策点区间(当前决策点所计算出来的区间左端点的 \(dp\) 值比原来更优)。记删完后 \(i\) 前面的区间为 \(lst\),此时仍然有两种情况:
-
\(i\) 将所有决策点都删掉了,或者 \(i\) 计算出来的 \(lst\) 右端点的决策值不如原本 \(lst\) 计算出来的优(\(lst\) 不会改变)。此时仍然细分成两种情况:
\(1.\) \(i\) 没有删掉任何一个决策点,此时直接退出(单调不降不意味着每个数都能成为最优决策点)。
\(2.\) 否则,直接将 \(i\) 插入到 \(lst\) 后面,即栈底即可。管辖区间为 \([lst.r+1,n]\)。
-
\(i\) 计算的右端点值比原本 \(lst\) 计算出来的值更优。此时虽然不会删除 \(lst\) 全部(否则已经删了),但是会删除 \(lst\) 的一部分。记这部分为 \([x,lst.r]\),那么显然 \([lst.l,x-1]\) 这一段都是 \(lst\) 更优。\(x\) 显然可以通过二分查找求出,那么只需要覆盖 \([x,n]\) 这一段后缀即可。
下面我们来计算时间复杂度:
-
对于每个决策点,其最多入栈出栈一次,时间复杂度 \(O(n)\)。
-
每个决策点更新后缀的时候需要二分,决策点数量为 \(n\),二分次数是 \(\log n\) 的级别,时间复杂度 \(O(n\log n)\)。
这也解释了为什么暴力删除复杂度是对的。
这样的话时间复杂度就是 \(O(n\log n)\),可以通过。虽然比斜率优化之类的 \(O(n)\) 差一些,但也很不错了。
UPD:二分栈的操作和队列是一样的,但是名字就叫二分栈(不太能理解给这个数据结构取名字的人)。
代码:
#include<bits/stdc++.h>
//#pragma GCC optimize("Ofast")
#define gt getchar
#define pt putchar
#define y1 y233
#define int long long
typedef long long ll;
//typedef __int128 lll;
typedef unsigned long long ull;
const int N=5e4+5;
using namespace std;
inline bool __(char ch){return ch>=48&&ch<=57;}
inline int read(){
int x=0;bool sgn=0;char ch=gt();
while(!__(ch)&&ch!=EOF){sgn|=(ch=='-');ch=gt();}
while(__(ch)){x=(x<<1)+(x<<3)+(ch-48);ch=gt();}
return sgn?-x:x;
}
template<class T>
inline void print(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);
}
template<class T>
inline void printsp(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(32);
}
template<class T>
inline void println(T x){
static char st[70];short top=0;
if(x<0)pt('-');
do{st[++top]=x>=0?(x%10+48):(-(x%10)+48),x/=10;}while(x);
while(top)pt(st[top--]);pt(10);
}
inline void put_str(string s){
int siz=s.size();
for(int i=0;i<siz;++i) pt(s[i]);
printf("\n");
}
int n,a[N],L,sum[N],dp[N];
struct Node{
int id,l,r;
Node(int _id=0,int _l=0,int _r=0):id(_id),l(_l),r(_r){}
}stk[N];
int head=1,tail=0;
inline int calc(int l,int r){
if(l>=r)return LONG_LONG_MAX;
int qwq=sum[r]-sum[l]+r-l-(L+1);
return dp[l]+qwq*qwq;
}
signed main(){
n=read(),L=read();
for(int i=1;i<=n;++i) a[i]=read(),sum[i]=sum[i-1]+a[i];
stk[++tail]=Node(0,1,n);
for(int i=1;i<=n;++i){
if(stk[head].r<i)head++;
dp[i]=calc(stk[head].id,i);
bool flag=0;
while(calc(stk[tail].id,stk[tail].l)>=calc(i,stk[tail].l))tail--,flag=1;
if(tail<head||calc(stk[tail].id,stk[tail].r)<calc(i,stk[tail].r)){
if(!flag)continue;
stk[tail+1]=Node(i,stk[tail].r+1,n),tail++;
}else{
int l=stk[tail].l,r=stk[tail].r,ans=0;
while(l<=r){
int mid=l+((r-l)>>1);
if(calc(stk[tail].id,mid)>=calc(i,mid))ans=mid,r=mid-1;
else l=mid+1;
}
stk[tail++].r=ans-1;
stk[tail]=Node(i,ans,n);
}
}
println(dp[n]);
return 0;
}