摘要:大家知道电感的阻抗为什么是\(jwL\)吗?滤波器的截止频率为什么是\(\frac1{2\pi RC}\)吗?本文将从复数的概念给大家推导出电感(容)的阻抗公式,并进一步以滤波器为例给大家介绍电路频率响应分析方法。

一、复数
我们在高等数学中学习了复数的概念:形如\(Z=a+bi\)的数称为复数,其中规定\(i\)为虚数单位,且\(a、b\)是任意实数;同时规定\(i^2=-1\)(在复平面中,\(i\)特指“逆时针旋转\(90^。\)角”的变换)。
复数\(Z=a+bi\)的模是\(Z\)点到复平面圆心处的距离:
复数\(Z=a+bi\)的幅角\(\varphi\)是复数在复平面中与X正半轴的夹角:
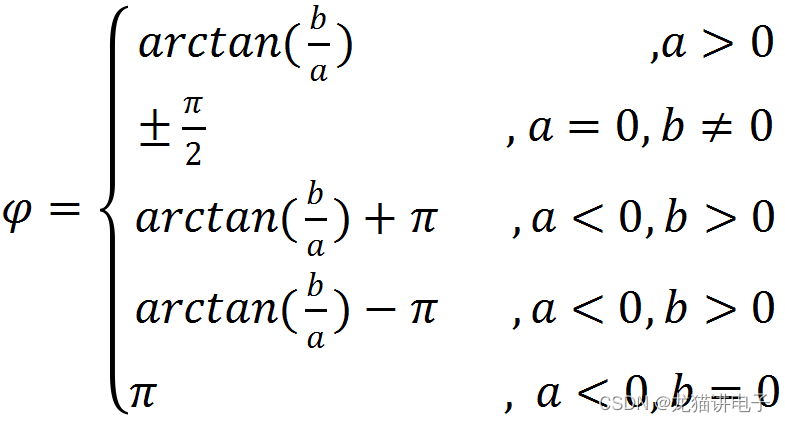
二、电感(容)阻抗公式推导
回到摘要中的问题:电感的阻抗为什么是\(jwL\)?
大家都知道电感最基本(也是最重要)的公式是:
\[U=L\frac{di}{dt}\tag{2} \]再根据傅里叶变换原理,我们的电信号都是可以用傅里叶级数展开,由无数的正弦波构成。所以假设电感电流为:
\[i=I_0\sin(wt)\tag{3} \]所以电感电压为:
\[U=L\frac{di}{dt}=LI_0w\sin(wt+\frac\pi2)\tag{4} \]电感电压除以电流就得到电感的阻抗:
\[Z_L=\frac ui=\frac{LI_0w\sin(wt+\frac\pi2)}{I_0\sin(wt)}=jwL\tag{5} \]说明:电感电压比电流相位超前\(90^。\),所以这里直接引入虚数单位\(j\)(在复平面中,\(j\)特指“逆时针旋转\(90^。\)角”的变换)。
同理,可推导出电容的阻抗为:
\[Z_C=\frac1{jwC}\tag{6} \]三、滤波器的频率响应分析
通过上述的推导发现电感(容)的阻抗是一个复数,所以用复数来分析电路将会非常方便;并且复数的模可以体现电路的幅频特性,复数的幅角可以体现电路的相频特性。
这是一个无源单级RC高通滤波器电路:
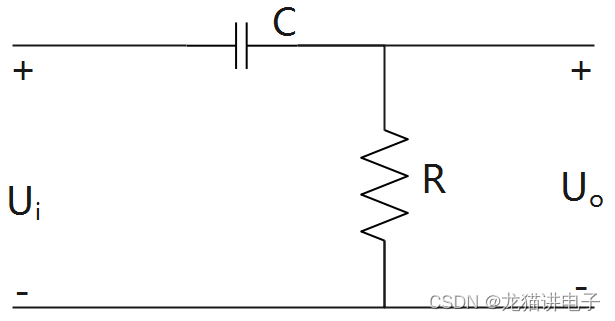
滤波器的增益为:
\[A_v=\frac{U_o}{U_i}=\frac R{R+\frac1{jwC}}=\frac{jwRC*(1-jwRC)}{(1+jwRC)(1-jwRC)}=\frac{(wRC)^2}{1+(wRC)^2}+\frac{jwRC}{1+(wRC)^2}\tag{7} \]滤波器的幅频特性为:
\[|A_v|=\frac{wRC\sqrt{1+(wRC)^2}}{1+(wRC)^2}=\frac {wRC}{\sqrt{1+(wRC)^2}}\tag{8} \]使用Matlab绘制高通滤波器的幅频特性曲线:
w = linspace(0,99,100)
R = 10
C = 0.01
y =w.*R.*C./sqrt(1+(w.*R.*C).^2)
plot(w,y)
同时我们还可以求解出高通滤波器的截止频率(\(A_v=\frac{\sqrt2}2A_{vmax}\)):
\[\because\frac{\sqrt2}2=\frac {wRC}{\sqrt{1+(wRC)^2}}\tag{9} \]\[\therefore w=\frac1{RC}\tag{10} \]\[\therefore f_L=\frac1{2\pi RC}\tag{11} \]下面再让我们看一个例子,电路图如下:
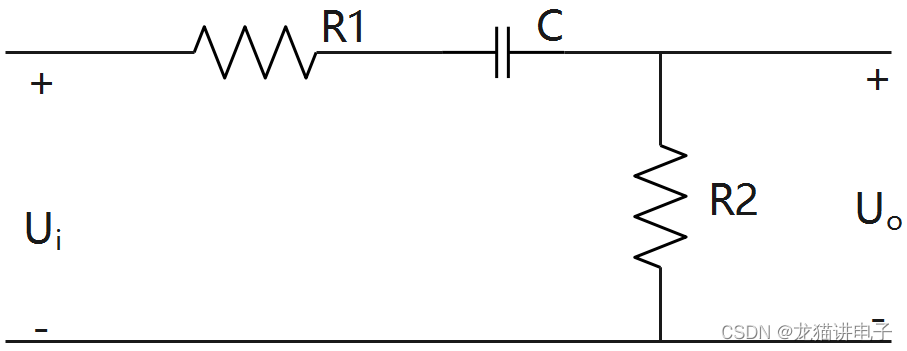
按照上述方法计算滤波器的增益:
\[A_v=\frac {R_2}{R_1+R_2+\frac1{jwC}}\tag{12} \]滤波器的幅频特性为:
\[\frac1{|A_v|}=\frac{\sqrt{(R_1+R_2)^2+\frac1{(wC)^2}}}{R_2}\tag{13} \]\[\therefore |A_v|=\frac{R_2}{\sqrt{(R_1+R_2)^2+\frac1{(wC)^2}}}\tag{14} \]所以滤波器的截止频率为:
\[f_L=\frac1{2\pi \sqrt{2{R_2}^2-(R_1+R_2)^2}*C}\tag{15} \]为什么举这个例子呢?一是因为这个电路网络非常重要,\(R_1\)可以看作前级电路的输出阻抗,\(R_2\)可以看作后级电路的输出阻抗或负载,C为前后级电路的耦合电容;二是因为大多数人会自然而然地以为该电路网络的截止频率应该是\(f_L=\frac1{2\pi (R_1+R_2)C}\),所以我就在这里给出推导过程,消除大家的误解。
电路设计中的网络结构多种多样,有容性负载,也有感性负载,但只要掌握上述推理方法,总能拨开云雾见天日,守得云开见月明。
标签:滤波器,电感,频率响应,frac,wRC,分析方法,tag,frac1 From: https://www.cnblogs.com/wcat/p/16759617.html