难度2
eeeeeeeee比较有意思的一道题目。一开始看到删除,有一个很经典的trick,就是将删除变成插入,倒序处理。然后发现不会做了。然后巨佬lyc说可以用cdq分治,将时间变为第三个关键字,这样也就不用倒序处理了。考虑求出删除某个数后对逆序对个数产生的贡献,在加入了时间戳之后i,j为逆序对的条件变为
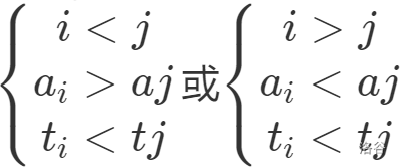
所以用两个cdq分治处理即可
#include<bits/stdc++.h>
using namespace std;
struct node{
long long a,b,c,ans;
}a[100005];
long long n,m,x,d[100005],mp[100005],sum=0;
bool cmp1(node x,node y){
return x.a<y.a;
}
bool cmp2(node x,node y){
return x.b<y.b;
}
bool cmp3(node x,node y){
return x.c<y.c;
}
long long lowbit(long long x){
return x&(-x);
}
void update(long long x,long long ad){
while(x<=n){
//cout<<x<<endl;
d[x]+=ad;
x+=lowbit(x);
}
}
long long getsum(long long x){
long long ans=0;
while(x){
ans+=d[x];
x-=lowbit(x);
}
return ans;
}
void cdq1(long long l,long long r){
if(l==r) return;
long long mid=(l+r)>>1;
cdq1(l,mid);cdq1(mid+1,r);
sort(a+l,a+mid+1,cmp2);
sort(a+mid+1,a+r+1,cmp2);
long long i,j=mid+1;
for(i=l;i<=mid;i++){
while(j<=r&&a[i].b>a[j].b){
update(a[j].c,1);
j++;
}
a[i].ans+=(getsum(m+1)-getsum(a[i].c));
}
for(i=mid+1;i<j;i++) update(a[i].c,-1);
}
void cdq2(long long l,long long r){
if(l==r) return;
long long mid=(l+r)>>1;
cdq2(l,mid);cdq2(mid+1,r);
sort(a+l,a+mid+1,cmp2);
sort(a+mid+1,a+r+1,cmp2);
long long i,j=mid;
for(i=r;i>=mid+1;i--){
while(j>=l&&a[i].b<a[j].b){
update(a[j].c,1);
j--;
}
a[i].ans+=(getsum(m+1)-getsum(a[i].c));
}
for(i=mid;i>j;i--) update(a[i].c,-1);
}
int main(){
cin>>n>>m;
for(long long i=1;i<=n;i++){
cin>>x;
a[i].a=i;
a[i].b=x;
a[i].c=m+1;
mp[x]=i;
}
for(long long i=1;i<=m;i++){
cin>>x;
a[mp[x]].c=i;
}
for(long long i=1;i<=n;i++){
sum+=(getsum(n)-getsum(a[i].b));
update(a[i].b,1);
}
memset(d,0,sizeof(d));
cdq1(1,n);
sort(a+1,a+n+1,cmp1);
cdq2(1,n);
sort(a+1,a+n+1,cmp3);
for(long long i=1;i<=m;i++){
cout<<sum<<"\n";
sum-=a[i].ans;
}
return 0;
}