Abstract
现有的GAE方法只能在链接预测任务上表现的很好,而它们在分类任务上的表现却相当有限,本文首次证明了GAE通过从图掩码的角度重新设计其关键的构建块,可以很好地适用于链接预测和分类场景,包括节点级和图级任务。我们提出的方法被称为是自监督图自动编码器(S2GAE)。具体来说,我们不是重建整个输入结构,而是随机掩码部分边,并学习用有效的掩码策略和表达解码器网络重建这些缺失的边。此外我们还从理论上证明了S2GAE可以被视为一个边缘级的对比学习框架
Introduction
目前的许多GAE只在链接预测任务上表现良好,但在节点或者图级分类任务较差,因为传统的GAEs可能会以牺牲结构信息为代价,过度强调接近信息
目前GraphMAE和GMAE的表现比较良好,但是失去了在链路预测任务上表现良好的能力,因为它们只关注重构节点特征,放弃了标准的网络结构重建,这对于推断缺失的链路至关重要。
目前存在的问题有:
- 目前图的拓扑结构被过分强调了。大多数现有的GAEs侧重于精确地重构输入图结构,即所有的成对连接,以保证邻居之间的拓扑紧密性。这种严格的要求可能会不利于捕获节点之间的结构信息,特别是对于包含冗余和有噪声信息的真实图。
- 没有损坏的图重构容易产生过拟合的数据,先前的GAE通常采用神经编码器,比如用GNN来学习节点表示。由于要恢复的目标连接在GNN中也被明确地用于节点嵌入,因此存在学习平凡解的风险,因为GNN在同质性假设下具有表达能力。然而破坏输入并试图恢复输入的掩码的自动编码器取得了巨大的成功
- 解码器的体系结构不能用于边的重建,特别是在边缘扰动之后。现有的GAE通常用多层感知机参数化其解码器,以根据节点的表示来估计节点之间的相似性。在传统的场景中,一个基于MLP的解码器可能足以建模节点之间的相关性。然而如果图的结构被破化,特别是当非平凡扰动进行时,GNN编码器将不可避免地受到影响,导致有噪声的节点表示。在这种情况下,普通的MLP解码器本身不够强大来重建边缘
本文的贡献:
受上述挑战的启发,我们提出了一个原理性的框架名称为自监督图自动编码器,用于可推广的图表示学习。S2GAE的工作原理是随机屏蔽图结构的一部分,然后学习用未屏蔽的图结构重建这些缺失的边。与传统的GAE相比,S2GAE也侧重于输入图的重构,但在模型输入、训练目标
和解码器体系结构上存在差异。关键的创新在于三个视角的新设计,共同释放了GAE的泛化能力。具体来说,S2GAE在很大程度上受益于以下关键设计:
- 掩码图构造:与大多数以重建原始图结构为目标的GAE不同,S2GAE侧重于使用部分图结构重建掩码边,通过适当的掩码策略和解码器网络,图掩码可以显著改善GAEs
- 方向感知图形掩码:除了标准的无向掩码策略之外,我们还设计了一种新的替代有向掩码(DM),将边缘视为双向的。DM为稀疏图提供了非平凡和有意义的自监督训练目标,并有利于分类任务
- 互相关解码:我们没有直接使用编码器的输出嵌入来进行边缘重建,而是提出了一个定制的互相关解码器,在多粒度中突出锚定边的头和尾节点之间的共同主题,从而参数用于重建的信息边缘表示。这种设计能够在广泛的掩码率范围中持续地表现的更好
Method
模型的总体结构如下:
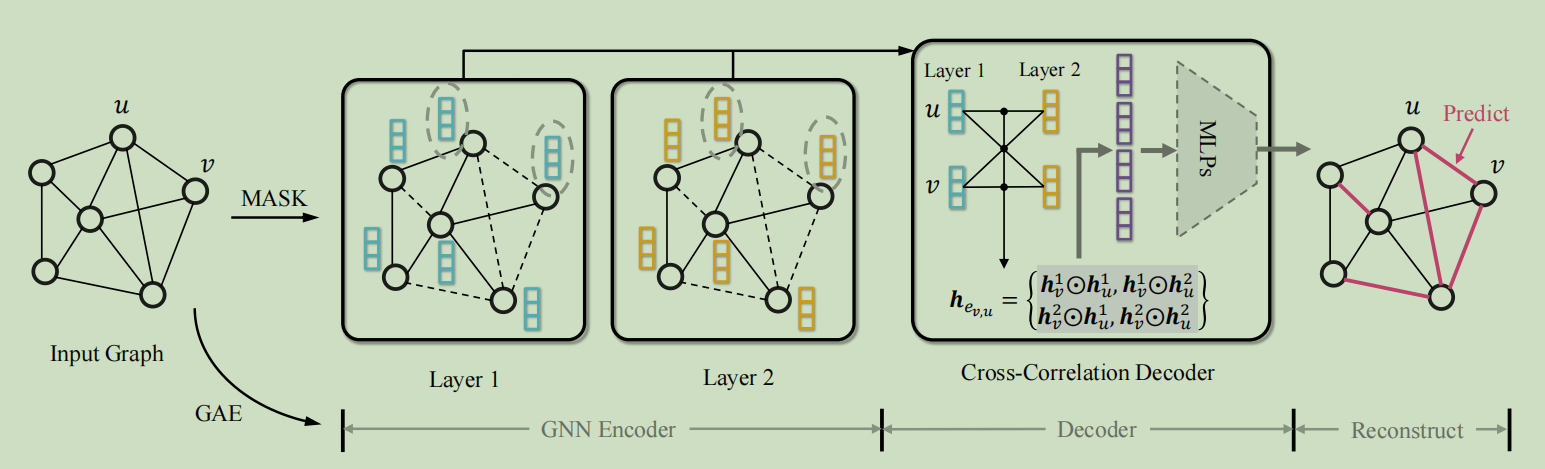
提出的S2GAE架构如下:给定一个图,首先应用方向感知图的掩码策略对其进行干扰,得到扰动图和掩码边集。然后将扰动图输入GNN编码器,产生隐藏表示。接下来设计一个定制的互相关解码器,通过从多粒度表示中捕获其末端节点的互相关,来重建这些掩码边缘。最后通过最大化掩码边集的可能性,对整个框架进行端到端训练。
传统图编码器与S2GAE
传统的GAE旨在学习一个编码器,将图映射为一个嵌入矩阵,也就是将每一个节点映射为一个d维度的嵌入矩阵,并且解码器是是从嵌入中重建网络结构,也就是恢复图的边,GAE的目标是重构输入网络结构,网络结构如下:
\(\mathbf{H}=f(\mathcal{V},\mathcal{E}),\quad\mathcal{E}^r=g(\mathbf{H})\)
\(\mathcal{E}^r\)是重构的网络结构,重构的目标也可以是节点属性
S2GAE的创新之处在于方向感知图掩码策略和互相关解码器网络。前者有助于生成有效且有意义的自监督信号,用于输入扰动和目标重建,而后者通过捕获两端节点的多粒度特征之间的互相关来帮助更准确的边预测
扰动图输入
我们扰动图结构,利用其中一部分作为编码的输入,采用图掩码的方式来扰动输入图。
\(G_{perb}=(\mathcal{V},\mathcal{E}_{remain}),\quad\mathcal{E}_{remain}=\mathcal{E}-\mathcal{E}_{mask}\)
实现过程中采用均匀的随机抽样,而不是生成掩码的边集
目前传统的均匀采样相邻节点进行边掩码不是最优的,因为数据的稀疏性,在边掩码时需要考虑图的特征。于是提出了两种方向感知图掩码策略
- 无向掩码,将节点u和v认为是无向的,进行随机采样后所得的边缘掩码集也是无向的
- 有向掩码,将图中的连接视为是有向的,得到的边缘掩码集也是有向的
我们发现最佳的图掩码策略与图形统计和下游任务有关,如果网络非常密集或者有冗余的信息,那么最好采用无向掩码,如果图很稀疏,那么可以采用有向掩码
GNN 编码器
S2GAE将扰动图提供给GNN编码器,编码器的节点表示\(\{\mathbf{h}_v^{(1)},\mathbf{h}_v^{(2)},\cdots,\mathbf{h}_v^{(K)}\}\)不可避免地会产生噪声,之后在下一节介绍一个特定的互相关解码器来解决这个问题并提高重建能力
互相关解码器
给定一个边和它们的隐藏表示,现有的GAE通常将解码器网络定义为其嵌入的内积,或者使用MLP来进行嵌入连接。但是在利用扰动图作为输入时,具有较高的屏蔽比,直接应用标准的解码器结构是相当有限的,这种限制是因为掩码后的图结构不完整导致的
我们提出了一种新的互相关解码器来明确地捕获不同粒度的两端节点之间的互相关相似性,形式上,给定节点u,v的隐藏表示\(\{\mathbf{h}_v^{(k)},\mathbf{h}_u^{(k)}\}_{k=1}^K\),我们生成它们的交叉表示
元素相乘是为它们的相互关系建模的有效方法,因为它可以突出显示公共属性和差异信息,\(\mathbf{h}_{e_{v,u}}\)的大部分元素将为0或者小值,只保留两个节点之间高度相关的元素,这有助于后续的边缘预测。
在获得边缘的互相关表示后,我们采用MLP层来预测其存在的概率。我们的互相关解码器可以过滤出不一致的和不必要的信息,并帮助\(g(\cdot)\)基于这些共同的和信息丰富的特征做出预测
为什么S2GAE是可推广的
设\(g(v,u)\)为节点v和u的估计链路概率。S2GAE的训练目标是重建掩码边缘,损失函数为:
\[\mathcal{L}=-\frac1{|\mathcal{E}_{mask}|}\sum_{(v,u)\in\mathcal{E}_{mask}}\log\frac{\exp(g(v,u))}{\sum_{z\in\mathcal{V}}\exp(g(v,z))} \]与对比学习的联系
我们发现S2GAE实际上优化了一个边缘感知的对比学习目标。让\(h_{v,i}\)和\(h_{v,j}\)表示v在两种增强策略下的表示,标准的水平对比学习损失表述为:
\[\ell_v=-\log\frac{\exp(\sin(\mathbf{h}_{v,i},\mathbf{h}_{v,j})/\tau))}{\sum_{v^{\prime}=1,v^{\prime}\neq v}^N\exp(\sin(\mathbf{h}_{v,i},\mathbf{h}_{v^{\prime},j})/\tau))} \] 标签:mathbf,论文,笔记,解码器,mathcal,掩码,S2GAE,节点 From: https://www.cnblogs.com/anewpro-techshare/p/18026380