2024.01.05
CWS - C0452B - 叉集合
搬自 ZR 2022 省选联测 Day 5?
Task 1.
考虑对于 \(0\le a\le b\le c\) 有 \(a\oplus c \ge \min (a\oplus b,b\oplus c)\)。
因为对于 \(a\oplus c\) 的最高位的 \(1\),\(a\oplus b\) 和 \(b\oplus c\) 中应该恰好有一个这位为 \(0\),所以得证。
Task 2.
然后其次另外的就是 \(b-a\le b \oplus a\)。
显然,由异或的性质所以可以将其看作不进位的加法或者不补位的减法,所以得证。
然后我们用两个基本的 Task 来解决这个问题。
对于 Task 1.
可以知道 \(S\) 中的数一定只有相邻的数才有贡献。
对于 Task 2.
对于一个数对 \((i,j)\) 其实只有一些必要的 \(x\) 使得 \((i+x)\oplus(j+x)\) 最小,实际上就是考虑以 \(x\) 制出 \(\mathrm{f}(x)=(i+x)\oplus(j+x)\) 这样一个函数,记录一个集合 \(X\) 为必要的 \(x\) 的集合,有 \(\forall x'<x:\mathrm{f}(x')> f(x)\)。
实际上应该有 \(X\sube \{x|x=\min\{a|\mathrm{P}(a)\}\}\),其中 \(\mathrm{P}(a):2^k\mid (i+a) \lor 2^k \mid (j+a),k\in \N\)。
说人话就是 \(x\) 一定要满足一个条件就是 \((i+x)\) 或 \((j+x)\) 的后 \(k\) 位为 \(0\),且 \(x\) 是满足前者的最小值。
考虑 \((i+x)\) 的后 \(k\) 位为 \(0\)。
这时如果 \(x\) 增加,\(j+x\) 产生了进位向 \(k+1\) 位,那么就考虑到 \(j+x\) 和后 \(k+1\) 位为 \(0\) 的情况。
否则考虑后 \(k\) 位,增加前的贡献应该是 \((j+x)\) 后 \(k\) 位,设为 \(y\),增加后贡献应该是 \((x+\Delta x) \oplus (j+(x+\Delta x))\) 的后 \(k\) 位,设为 \(y'\)。根据 Task 2. 应该有 \(y\le y'\) 。
所以可以用 \(\textrm{set}\) 来维护相邻的贡献以及二元组 \((x,(i+x) \oplus(j+x))\)。
然后就完了,剩下的应该都会。
2024.01.07
Atcoder Xmas Contest 2022 H - Happy Game
直接粘贴自己的题解了。要题意的可以去”题解“合集里找。
在下文中计数的所有相关概念中不包括初始点 \(u\) 。
如果 B 每次都可以染色两个点,那么答案就很好算了。但是有时候 B 只能染一个点,我们把这种情况称为“卡住了”,称在某个点卡住了则说明在这个情景下 B 下一步只能染这一个点。
假设 A 选择了 \(u\) 点。
会发现原问题相当于是求 B 在最优策略下会有多少次被卡住。
考虑到在 B 的最优策略这一条件下,那么卡住的情况一定不会发生在点双的内部,这是比较显然的,否则一定可以通过简单的调整使得其不会被卡住。
所以有:
Task 1. B 卡住的情况一定会发生在点双的边界上。
令 \(\mathrm{dis}(x,y)\) 表示原图上 \(x\) 与 \(y\) 的最小距离,\(\mathrm{C}(x,d)\) 表示距离 \(x\) 不超过 \(d\) 的点的个数(如上文所说,不包括 \(u\) 点)。
设第一次卡住卡在了 \(v\) 点,染完 \(v\) 后一共染过 \(d\) 次操作,应有 \(\mathrm{dis}(u,v) \le d\)。
实际上到现在我们已经染了 \(2d - 1\) 个点。
Task 2. 第一次被卡住的必要条件应该是 \(\mathrm{C}(u,\mathrm{dis}(u,v))=2d - 1\)。
由 Task 1 可知 \(v\) 应该是一个割点,所以想象中把 \(v\) 点删去后的包含 \(u\) 的连通块(即下文的“包含 \(u\) 的连通块”)大小 \(\ge \mathrm{C}(u,\mathrm{dis}(u,v))\),又因为连通以及第一次卡住这些条件的限制可知:
如果 \(\mathrm{C}(u,\mathrm{dis}(u,v)) < 2d - 1\) 则显然 \(v\) 不可能是第一个被卡住的点,因为就算每次染两个点把这个包含 \(u\) 的连通块染满了也没有 \(d\) 次操作。
如果 \(\mathrm{C}(u,\mathrm{dis}(u,v)) > 2d - 1\) 则说明包含 \(u\) 的连通块中应该还有可以染的点,是所以 \(v\) 在最优策略下一定不会被第一个卡住。另外这里说一下,\(v\) 的被卡住一定不可能是主动的,即在有点可以染时故意不染,因为一定会更劣,考虑一下一般情况就知道了。
同样可知的是:
Task 3. 我们染 \(v\) 点以前包含 \(u\) 的连通块应该已经被染满了。
这启发我们依次被卡住的点 \(a_1,a_2,\cdots,a_k\) 应该在一条链上,且 \(\mathrm{dis}\) 应该越大越好,因为走的越远,中途可以用来防止被卡住的点就越多。
设 \(d_0\) 为最小的满足 \(c_{d_0}=2d_0-1\) 的值,则希望 \(\mathrm{dis}(u,v)= d_0\),发现一定可以取等(这个比较好理解),否则可以不被卡住。其实也就相当于是从 \(u\) 到 \(v\) 的最短路径上的点参与了每一次染色,即每一次染色时总会有一个这条路径上的点被染黑。
所以我们由此得出了 B 的最优策略:
每次找到 \(\mathrm{dis}\) 最小的满足 \(\mathrm{C}(u,\mathrm{dis}(u,v))=2\mathrm{dis}(u,v) - 1\) 的 \(v\) ,显然 \(v\) 是唯一的,否则 \(\mathrm{dis}\) 一定不是最小的,那么可知 \(a_1=v\);然后我们再找到这之后 \(\mathrm{dis}\) 最小的满足 \(\mathrm{C}(u,\mathrm{dis}(u,v'))=2\mathrm{dis}(u,v') - 2\) 的点(因为已经有一次操作只染了一个点),可知 \(a_2=v'\),以此类推。
所以最后一次卡住的点 \(a_k\) 我们记为 \(a\),则应该有 \(\mathrm{C}(u,\mathrm{dis}(u,a)) = 2\mathrm{dis}(u,a) - k\)。所以可知 \(k = 2\mathrm{dis}(u,a) - \mathrm{C}(u,\mathrm{dis}(u,a))\)。
答案应该是 \(\lceil \frac{n-1-k}{2} \rceil\)。
那么考虑如果有一个 \(a'\) 不为 \(a\),一定是整个操作中有不合法行为的,即在该染一个点时染了两个点,或者没有考虑卡没卡住,所以答案会偏小。
所以再把 A 的最优策略考虑进来,我们求答案,相当于求 \(k_{\max}=\max_u\max_a\{2\mathrm{dis}(u,a) - \mathrm{C}(u,\mathrm{dis}(u,a))\}\)。
好耶 \(O(n^2)\) 暴力启动!
我们将外层的两个 \(\max\) 交换,显然求值不变。
那么相当于是对于 \(a\) 来找 \(u\)。考虑因为 \(a\) 一定是一个割点 (Task 1),所以 \(u\) 一定在割掉 \(a\) 所剩下的连通块当中。由 Task 3 可知,整个包含 \(u\) 的连通块应该都会被染满,所以我们就确定了 \(\mathrm{C}(u,\mathrm{dis}(u,a))=|S(u)|\),其中 \(S(u)\) 表示包含 \(u\) 的连通块的大小。
所以我们相当于在 \(S(u)\) 中找到一个 \(\mathrm{dis}\) 最大的点就行了。
那么换一种思考方式,考虑存在一个 \(v\),使得割去 \(a\) 后 \(u,v\) 不连通,\(v\) 可以等于 \(a\)。
那么我们可以在关于 \(v\) 的 bfs 树上遍历,找到 \(a\) 点为点双边界,那么关于 \(v,a\) 的最优的 \(u\) 应该是 bfs 树上 \(a\) 子树内最深的点。
那考虑是否可以找到常数级别个数的 \(v\) 使得可以找到最优的 \(a,u\) 呢?
答案是可以的。
Task 4. \(v \in \{p,q\}\),其中 \(p,q\) 为原图的圆方树上直径的两个端点(一定是原图中的点)。
证明:
考虑反证,讨论不合法的情况。
这里的 \(\mathrm{dis}\) 均只考虑路径上的圆点。
第一种情况是,\(p,q\) 之间的路径与 \(u,a\) 之间的路径没有交,结合限制,应该长这样:
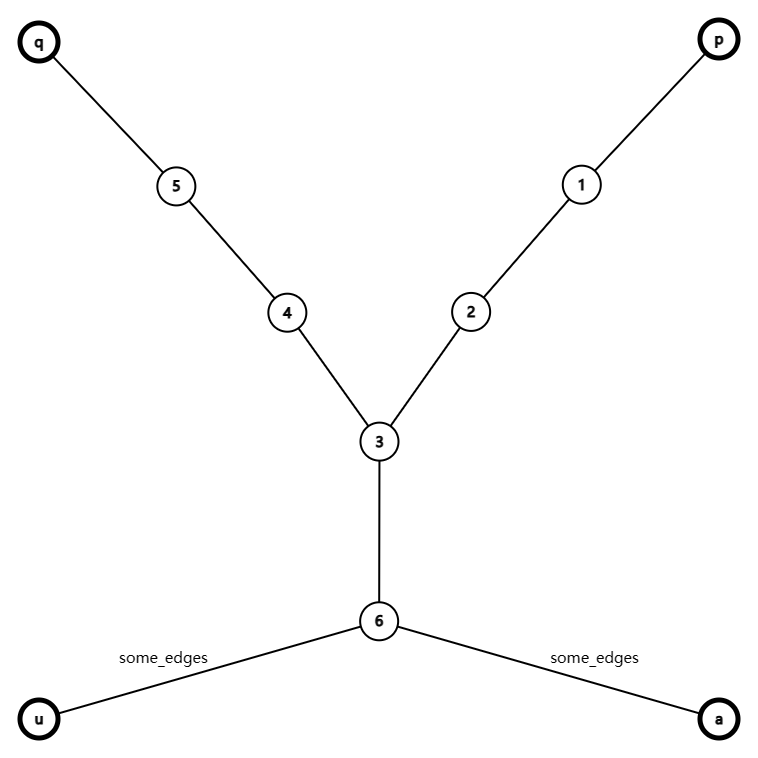
那么会发现因为 \(\mathrm{dis}(p,q) \ge \mathrm{dis}(u,a)\),甚至从 \(u\) 染到 \(a\) 用的染色次数 \(d=\mathrm{dis}(u,a) \le \mathrm{dis}(p,q)\) ,所以可知 \(a\) 一定是不合法的而偏小,可以不计入答案。
第二种情况是,\(p,q\) 之间的路径与 \(u,a\) 之间的路径有交,结合限制,应该长这样:
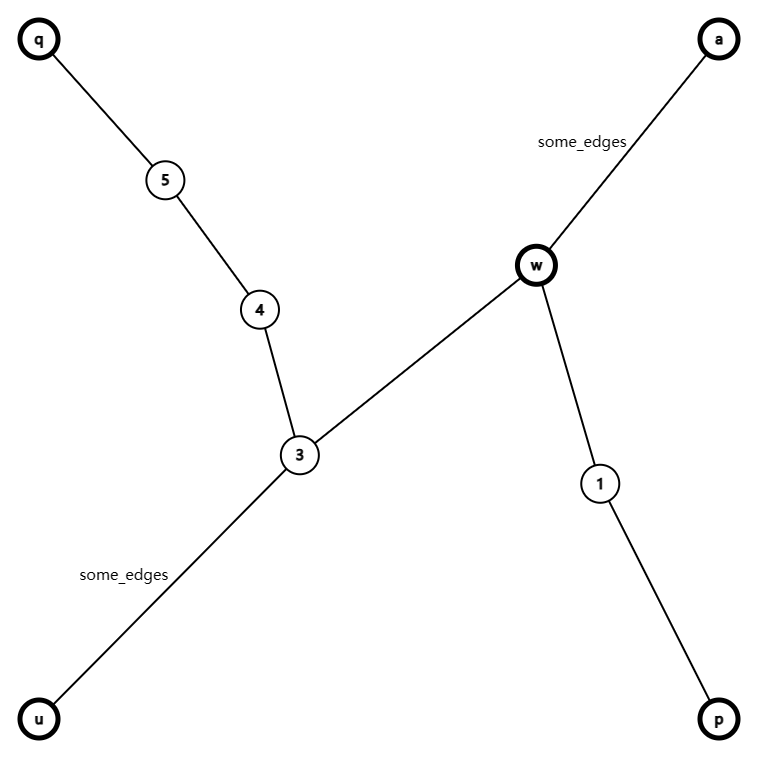
假设 \(w\) 是直径上最靠近 \(a\) 的点。那么会发现可以把 \(a\) 调整成 \(w\),此时依据我们得出的 \(k=2\mathrm{dis(\cdots)}-\mathrm{C}(\cdots)\) 的结论,这次调整在 \(\mathrm{dis}\) 上的变化是 \(-\mathrm{dis}(w,a)\),而在 \(\mathrm{C}\) 上的变化是 \(\ge \mathrm{dis}(w,p)\) 的(这个路径不会再被考虑进割去最优的 \(a\) 后 \(u\) 的连通块内了)。所以显然调整为 \(w\) 后贡献不劣。
即证。
所以只需要建出圆方树从两个端点各自求出最优解。
求的方法就是先 bfs 求出 \(\mathrm{dis}\),然后再在割点上找子树内点的最远距离和子树大小,按结论求最大值就可以了。
2024.01.08
CWS - C0454C - 重庆排列 / Codeforces - 698F - Coprime Permutation
基本思路感觉不太讲得出来,可以看别人的题解。
但是这个题必须做到 \(O(n)\),于是使用欧拉筛。并且为了小常数使用了异或 hash 判断质因数集合,就可以做到 \(O(n)\) 了,具体实现见代码。
对不起,我真的不会讲。
2024.01.09 ~ 2024.01.17
学习了 SA 和 SAM 并且做了一些题,题单可以在我的学习笔记中找到。题目比较简单并且比较套路,这里就不展开了。
2024.01.18
CWS - C0464A - 破烂森林
冷知识:设有向图图的邻接矩阵为 \(A\),出度矩阵为 \(D\),统计这个有向图的生成子图为内向基环树森林且每个环的大小均为奇数时 \(2^k\) 的和,其中 \(k\) 是环的个数。那么这时的答案显然为 \(|A+D|\) 即 \(\det(A+D)\) 的值。
证明 设 \(B=A+D\)。
首先考虑枚举一个排列 \(p\),对于 \(p_i=i\) 的位置,出边任意选;否则钦定 \(i\) 出边为 \(p_i\)。对于这样一个排列在有向图中被选取的方案数为 \(\prod_{p_i=i} \deg_{out}\prod_{p_i\ne i} A_{i,p_i}=\prod_{i=1}^{n} B_{i,p_i}\)。
因为 \(p_i=i\) 时在摆烂随便选,所以每个环都有可能选到或者不选到,因此应该考虑容斥统计。
对于排列 \(p\),钦定偶置换环个数为 \(v\),那么定义权值为 \((-1)^v\prod_{i=1}^n A_{i,p_i}\)。
这时可以证明排列的权值之和就是答案。
如果一种内向树森林的方案有 \(u\) 个奇环和 \(v\) 个偶环,那么根据我们对排列贡献的性质,把任意多个环换成各自指向自己的自环,这时各种换法就各自取走了各自容斥所需的部分,发现这个是没有交的。这个方案的贡献是:
\[\sum_{i=0}^u\sum_{j=0}^v\tbinom{u}{i}\tbinom{v}{j}(-1)^j=2^u\sum_{j=0}^v(-1)^j(\tbinom{v - 1}{j} - \tbinom{v - 1}{j - 1})=[v=0]2^u \]2024.01.25 ~ 2024.02
冬令营,鸽了。
标签:连通,01,卡住,2024,Task,做做,oplus,mathrm,dis From: https://www.cnblogs.com/imcaigou/p/18024402