[ARC003D] シャッフル席替え

标签：cnt frac int ARC003D tot 点数 席替 pi

这道题使用了蒙特卡罗方法。

蒙特卡罗方法是指使用随机数来解决计算问题的方法。他的工作原理就是两件事：不断抽样、逐渐逼近。

例如计算 \(\pi\)。

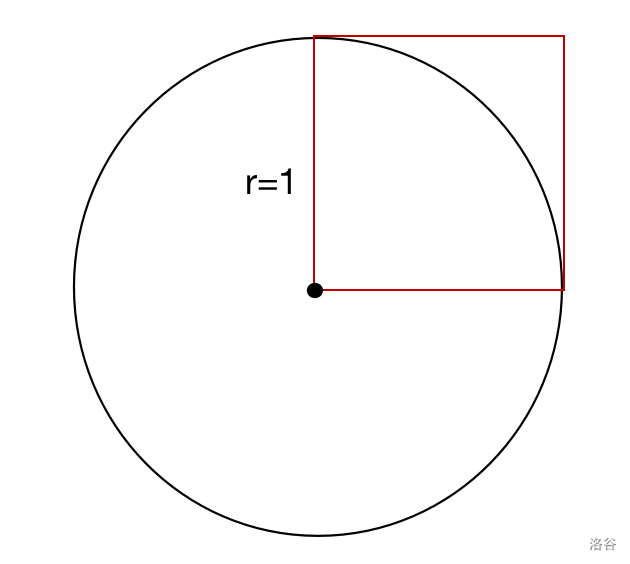
这样的一个圆，在它的右上角做一个正方形。

则圆的面积为 \(\frac{\pi}{4}\)，正方形的面积为 \(1\)。

现在向图中随机放点，则圆的面积比正方形的面积等于红点数比总点数。

记红点数为 \(r\)，总点数为 \(tot\)，即 \(\frac{\pi}{4}=\frac{r}{tot}\)。

所以 \(\pi=\frac{4\times r}{tot}\)。

回到本题，注意到 \(n\leq11,k\leq20\)，且精度限制范围大，考虑模拟。

输出满足条件的次数与总共次数的比值即可。

const int N = 15;
int n, m, k, a[N], b[N], f[N][N], g[N];
signed main() 
{
    cin >> n >> m >> k;
    R(i, 1, m) cin >> a[i] >> b[i], ++a[i], ++b[i], f[a[i]][b[i]] = f[b[i]][a[i]] = 1;
    mt19937 rnd(time(0));
    int p = 0, q = 0;
    R(t, 1, 3e6)
    {
        ++q;
        R(i, 1, n) g[i] = i;
        bool cnt = 0;
        R(i, 1, k)
        {
            int x = 0, y = 0;
            do 
            {
                x = rnd() % n + 1, y = rnd() % n + 1;
            } while (x == y); 
            swap(g[x], g[y]);
        }
        R(i, 1, n - 1) cnt |= f[g[i]][g[i + 1]]; cnt |= f[g[n]][g[1]];
        p += !cnt;
    }
    printf("%.8Lf", (long double)p * 1.0 / q);
    return 0;
}

标签：cnt,frac,int,ARC003D,tot,点数,席替,pi
From： https://www.cnblogs.com/cyyhcyyh/p/18018310