什么是 Binary Indexed Trees?
就是树状数组啦。树状数组,是一种高级数据结构,用于高效地解决某一类问题。
那么这一类问题是什么呢?那么让我们一起来看一下:
问题引入
给定一个序列 \(a\),给定 \(Q\) 个 \(l,r\),求 \(\sum_{i=l}^r a_i\)。
这一类问题,我们明显可以暴力枚举,时间复杂度为 \(\Theta(\sum_{i=1}^Q r-l+1)\)。
明显,若 \(l,r\) 过于大,这样也解决不了,因此有了前缀和。
前缀和,是用来统计前 \(\sum_{i=1}^j a_i\),也就是说,回答每一次查询只需要 \(\Theta(1)\) 即可,即为 \(a_r-a_{l-1}\)。
这种算法在此问题已经算很高级了,但是如果我们改一下:
给定一个序列 \(a\),给定 \(Q\) 个 操作,每次给定 \(opt,l,r\),分如下 \(2\) 种操作:
-
\(opt=1\),将 \(a_l\) 增加为 \(r\)。
-
\(opt=2\),求 \(\sum_{i=l}^r a_i\)。
这时,暴力枚举最坏的时间复杂度变为了 \(\Theta(\sum_{i=1}^Q r_i-l_i+1)\),前缀和的最坏时间复杂度则变成了 \(\Theta(Qn)\)。
因此,我们有了树状数组或者线段树,虽然它们对于每次操作都是 \(\mathcal O(log n)\),但是线段树应用范围更广,但是这里采用树状数组解决,因为它实现更简单。但是等你都熟练了之后,你会发现,只不过是多了几行代码而已。。。
树状数组的引用
首先我们需要了解一下二进制。
我们知道,任意一个整数 \(x\) 都可以分为 \(2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_m}\)。
设 \(a_1>a_2>a_3>\ldots>a_m\),则最多可以分解为 \(\log n\) 的区间。
-
区间 \(1\) 长度为 \(2^{a_1}\),表示范围为 \([1,2^{a_1}]\)。
-
区间 \(2\) 长度为 \(2^{a_2}\),表示范围为 \([2^{a_1}+1,2^{a_1}+2^{a_2}]\)。
\(\ldots\ldots\ldots\ldots\)
- 区间 \(m\) 长度为 \(2_{a_m}\),表示范围为 \([2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_{m-1}}+1,2^{a_1} + 2^{a_2} + 2^{a_3} + \ldots + 2^{a_m}]\)。
因此,区间 \([l,r]\) 的长度为 \(2^{\texttt{r 的二进制末尾 0 个数}}\),也就是 \(r\) 最右边的 \(1\) 所代表的数。
我们编程通常用 lowbit(x) 表示,计算方法为 \(x\operatorname{and}(x\operatorname{xor}(x-1))=x\operatorname{and}(-x)\)。
这其实涉及到计算机补码的知识,可以自己百度一下。
inline int lowbit(int x){
return x&-x;//有无括号无所谓啦。
}
树状数组是一种基于二进制思想的数据结构,用来维护序列的前缀和。
—— 网上的一句话。
也就是说,我们可以用 \(tree_i\) 表示 \(\sum_{i=x-\operatorname{lowbit(x)}+1}^x a_i\)。
那么我们不难得到如下图(非原创):
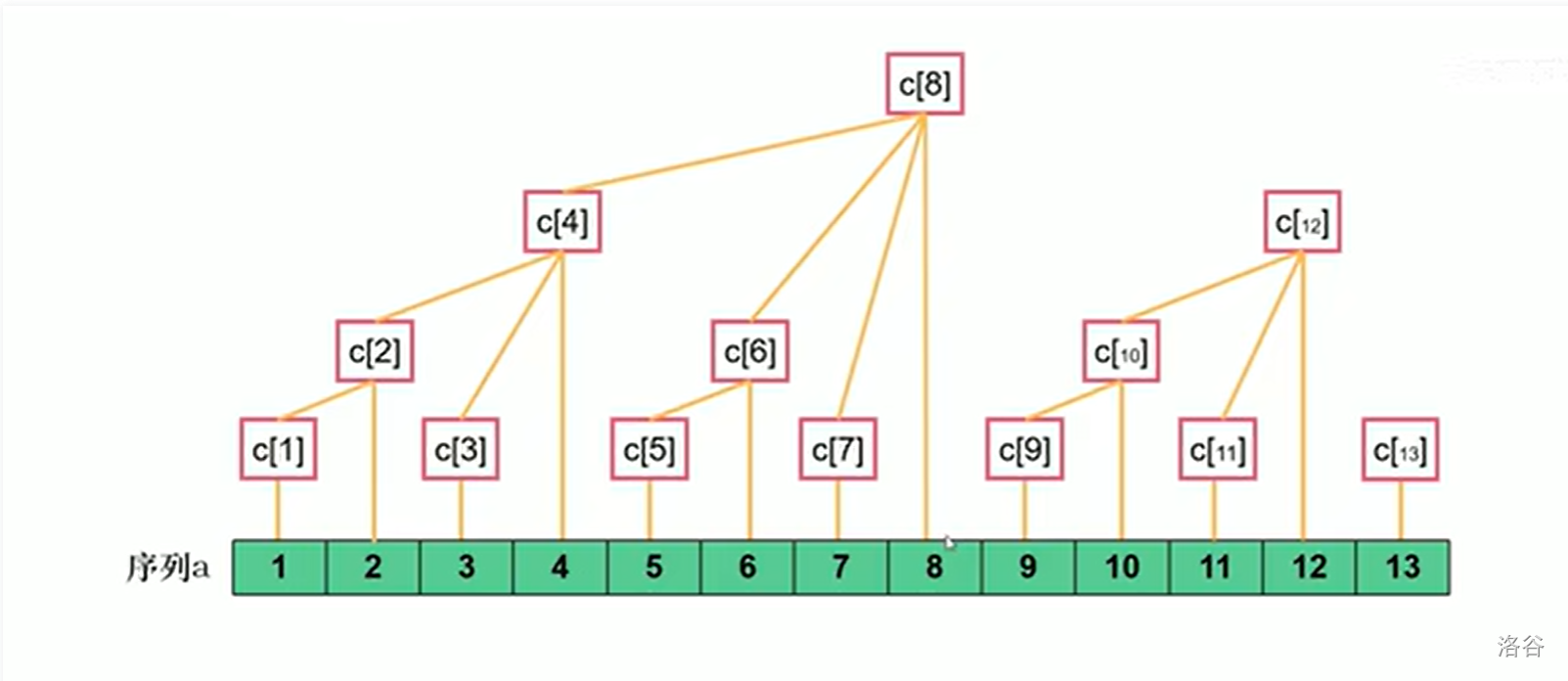
把 \(c\) 当成 \(tree\) 吧。。。
为什么 \(tree_8\) 连接了 \(tree_7,tree_6,tree_4\) 以及 \(a_8\) 呢?首先 \(a_8\) 不用解释了,然后 \(7+lowbit(7)=8\),\(6+lowbit(6)=8\),\(4+lowbit(4)=8\)。
单点修改
如果对于 \(a_x\) 进行修改,那么 \(tree_x\sim tree_n\) 的值都会进行变化,因此可以用一个循环将满足条件的 \(tree_y\gets tree_y+a_i\):
inline void updata(int k,int x){
for(;k<=n;k+=lowbit(k))//每次增加 lowbit(k)。
tree[k]+=x;
}
区间查询
很明显,最好理解,每次减少 \(lowbit(i)\),并且累加 \(tree_i\) 即可。
inline int query(int k){
int sum=0;
for(;k>0;k-=lowbit(k))
sum+=tree[k];//累加,不理解建议看看前面的 tree[i] 的表示。
return sum;
求区间和就 \(query(r)-query(l-1)\) 就行啦(就是前缀和思想)。
初始化
很简单,每次 \(updata(i,a_i)\) 即可,时间复杂度为 \(\Theta(n\log n)\)。
但是还有一种 \(\Theta(n)\) 的方法,考虑每个节点对父亲节点的贡献为 \(tree_i\),因此代码如下:
for(int i=1;i<=n;i++){
tree[i]+=a[i];
if(i+lowbit(i)<=n) //不要越界。
tree[i+lowbit(i)]+=tree[i];
例题
以下代码都是本蒟蒻早期时大的代码,没有优化,纯 cin,cout。
就是上面说的两种操作,直接背模板即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,q,x,y,a,opt,tree[N];
inline int lowbit(int x){//lowbit 函数求解。
return x&-x;
}
inline int query(int k){//模板。
int sum=0;
for(;k>0;k-=lowbit(k)) sum+=tree[k];
return sum;
}
inline void update(int k,int x){//模板。
for(;k<=n;k+=lowbit(k)) tree[k]+=x;
}
signed main() {
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>a;
update(i,a);//建立树状数组。
}
while(q--){
cin>>opt>>x>>y;
if(opt==1) update(x,y);//单点修改。
else cout<<query(y)-query(x-1)<<endl;//区间查询。
}
return 0;
}
这其实涉及到两种操作,即为区间修改以及单点查询。
如果还是用上面的方法去做,时间复杂度可能会达到 \(\Theta(Qn)\)。
所以这种方法是不可行的。
考虑差分,没学过建议学一学。
比如:\(a=[1,2,6,11,12,16,15]\),那么差分数组 \(b=[1,1,4,5,1,4,-1]\)。(逃
也就是说,\(b_i = a_i - a_{i-1}\)。
很好证明,\(a_i = \sum_{j=1}^i b_j\),因为 \(a_i - a_{i-1} + (a_{i-1} - a_{i-1}) + \ldots + (a_2 - a_1) + (a_1-[a_0\to 0]) = a_i\)。
所以说,我们可以用树状数组维护差分数组,并不用维护原数组。
但是将 \([l,r]\) 都加上 \(x\) 怎么操作呢?我们可以举了栗子:
比如:\(a=[1,4,9,16,25,36,49]\),\(b=[1,3,5,7,9,11,13]\),将 \([2,5]\) 都加上 \(5\),那么原数组为 \([1,9,14,21,30,36,49]\),差分数组就为变为 \([1,8,5,7,9,6,13]\)。
仔细观察,我们发现:\([l,r]\) 区间内差分数组 \((l,r]\) 内的没有变,然而 \(b_l\gets b_l+x\),\(b_r\gets b_r-x\)。
设 \(i\) 在 \((l,r]\) 之间,则更改后 \(b_i = (a_i+x) -(a_{i-1}+x)=a_i-a_{i-1}\),不会发生变化。
但是 \(i=l\),\(b_i = (a_i + x) - (a_{i-1}) = a_i - a_{i-1}+x=b_i+x\);\(i=r+1\),\(b_i = a_i - (a_{i-1}+x)=a_i-a_{i-1}-x=b_i-x\)。
因此,我们只需要对两个端点进行单点修改即可。
update(l,x);//增加。
update(r+1,-x);//减少。
那么怎么输出呢?
因为 \(a_i = \sum_{j=1}^i b_j\),上面有证明,所以直接查询就行了(反正维护的是差分数组)。
\(\boxed{Code}\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,q,x,y,s,a[N],opt,tree[N];
inline int lowbit(int x){
return x&-x;
}
inline int query(int k){
int sum=0;
for(;k>0;k-=lowbit(k)) sum+=tree[k];
return sum;
}
inline void update(int k,int x){
for(;k<=n;k+=lowbit(k)) tree[k]+=x;
}
signed main() {
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>a[i];
update(i,a[i]-a[i-1]);//维护差分数组,O(n) 也可以,只不过 O(n log n) 更容易实现。
}
while(q--){
cin>>opt;
if(opt==1){
cin>>x>>y>>s;
update(x,s);
update(y+1,-s);//做两次正确的单点修改即为区间修改。
}
else{
cin>>x;
cout<<query(x)<<endl;//输出。
}
}
return 0;
}
一眼望去,就是求序列里逆序对的个数,于是乎我们 \(\mathcal O(n^2)\) T 了。
仔细看看数据,\(1\le n\le 5\times 10^5\)。
笔者有事,先走了。
笔者回来啦。
那么这类问题涉及到了树状数组的另一个作用:求逆序对!
由于原本的数组 \(a\) 过于庞大,我们考虑离散化。
将序列 \(a\) 从大到小排序,如果值相同则按照位置从大到小排序。
这样,相同的值就不会被统计逆序对了。
随后,我们考虑用树状数组维护:
-
已知,一开始,\(\forall tree_i= 0\)。
-
然后开始遍历,设当前值为 \(x\),位置为 \(v\)。
-
首先查询树状数组 \(v-1\) 的位置,查找大于 \(x\) 的数的个数(这样才能形成逆序对,即 \(a_i > a_j\))。
-
然后对 \(v\) 位置以及其后的 \(tree_y(y\leq v)\) 做 \(+1\) 操作,因为已经排序,所以该点对后面的贡献为 \(1\)。
时间复杂度为 \(\mathcal O(n\log n)\)。
\(\boxed{Code}\)
//笔者:可以复制哦。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,ans,tree[N];
struct node{
int num,pos;
};
node a[N];
inline bool cmp(node s1,node s2){
if(s1.num==s2.num) return s1.pos>s2.pos;
return s1.num>s2.num;
}
inline int lowbit(int x){
return x&-x;
}
inline int query(int k){
int sum=0;
for(;k>0;k-=lowbit(k)) ans+=tree[k];
return sum;
}
inline void update(int k){
for(;k<=n;k+=lowbit(k)) tree[k]++;//直接 ++。
}
signed main() {
cin>>n;
for(int i=1;i<=n;++i){
cin>>a[i].num;
a[i].pos=i;//记录位置。
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++) {
ans+=query(a[i].pos-1);//查询。
update(a[i].pos);//修改,做贡献。
}
cout<<ans<<endl;
return 0;
}
挺不错的,只不过是有一些性质。
我们都知道,异或的运算法则:相同则 \(0\),不同则 \(1\)。
因此如下性质:
- \(a \oplus a=0\)
(自己异或自己,二进制一模一样,每一位都相同,肯定是 \(0\))。
- \(a\oplus 0 = a\)
(相当于每一位都异或 \(0\),分情况讨论。设 \(a_i\) 表示 \(a\) 的二进制第 \(i\) 位,如果 \(a_i = 1\),则 \(1\oplus 0=1\),一样;若 \(a_i = 0\),则 \(0\oplus 0=0\),一样。所以 \(a\oplus 0 = a\))。
通过计算,设序列长度为 \(len\),则第 \(i\) 个数会出现 \(\sum_{j=1}^i (n-j+1) - (i-j)= \sum_{j=1}^i n-i+1 = i\times (n-i+1)\)。
分情况讨论:
-
如果 \(2\mid n\)。
-
如果 \(2\mid i\),则任何 \(2\mid i\) 的数出现的次数都是偶数次。
-
如果 \(2\mid (i+1)\),则 \(n-i+1\) 为偶数,则任何 \(2\mid (i+1)\) 的数都会出现偶数次。
-
-
如果 \(2\mid (n+1)\)。
-
如果 \(2\mid i\),则 \((n-i+1)\) 为偶数,则任何 \(2\mid i\) 的数都会出现偶数次。
-
若 \(2\mid (i+1)\),则两端都是奇数,奇数 \(\times\) 奇数 \(=\) 奇数,所以任何 \(2\mid (i+1)\) 的数都会出现奇数次。
-
因为偶数次为根据性质 \(1\) 抵消变为 \(0\),而 \(0\) 又会根据性质 \(2\) 完全没有作用,因此:
-
若 \(2\mid (r-l+1)\),则答案为 \(0\)。
-
若 \(2\mid (r-l)\),则答案为 \(a_l \oplus a_{l+2} \oplus a_{l+4}\oplus\ldots \oplus a_r\)。
这样该怎么求呢?我们可以开两个树状数组维护右端点分别为奇偶数的情况呀!
那么原本的加法运算怎么办呢?那都改为异或运算不就好了嘛!
\(\boxed{Code}\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+10;
int n,q,x,y,opt,ans,a[N];
inline int lowbit(int x){
return x&-x;
}
struct node{//定义在结构体更方便。
int xx[N];
inline int query(int k){//区间查询。
int sum=0;
for(;k>0;k-=lowbit(k)) sum^=xx[k];
return sum;
}
inline void update(int k,int x){//单点修改。
for(;k<=n;k+=lowbit(k)) xx[k]^=x;
}
};
node tree[3];
signed main() {
cin>>n>>q;
for(int i=1;i<=n;++i){
cin>>a[i];
tree[i&1].update(i,a[i]);//建树。
}
while(q--){
cin>>opt>>x>>y;
if(opt==1){
tree[x&1].update(x,a[x]^y);//别忘了修改哈,把 a[x] 修改为 y 就是异或 a[x]^y。
a[x]=y;
}
else
if(!((y-x+1)&1)) cout<<"0\n";//区间个数为偶数,答案为 0.
else cout<<((tree[x&1].query(x-1))^(tree[x&1].query(y)))<<endl;//否则维护即可。
}
return 0;
}
未完待续。。。
标签:Binary,浅谈,int,lowbit,sum,tree,数组,Indexed,inline From: https://www.cnblogs.com/2021zjhs005/p/18014140