对网络的定义进行扩展,我们可以得出一堆奇奇怪怪的网络。
上下界
令 \(Max_e\) 为边 \(e\) 的流量上界,\(Min_e\) 为边 \(e\) 的流量下界,一条边的流量 \(f_e\) 要满足 \(Min_e \le f_e \le Max_e\),除此之外和普通网络流定义相同,可以发现,普通的网络就是下界为 \(0\) 的网络。
无源汇
顾名思义,如果抛弃源汇点的设定,对每一个点,都要满足流量守恒,即入流等于出流,那么这就是无源汇的网络流。
有源汇的网络可以通过添加 \(T \rightarrow S\),下界为 \(0\),上界为 \(INF\) 的边,变成无源汇网络。
这是一张无源汇上下界网络。
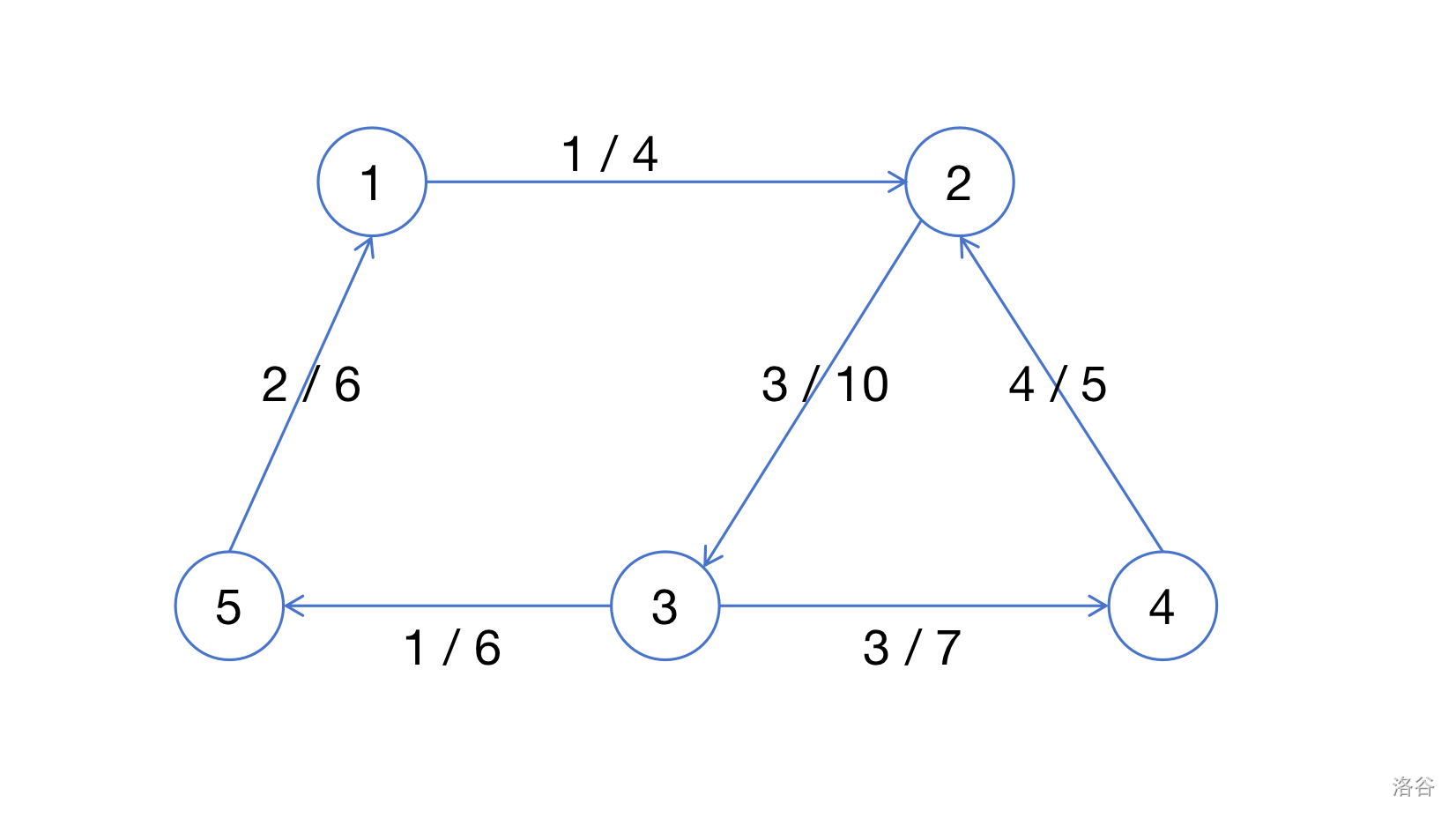
解决扩展网络流的核心就是:转化为普通网络流问题。
无源汇上下界可行流
这个模版是之后的基础,我们也借此来探究如何将带下界的网络流转化成普通的(下界为0)网络流。
首先,每一条边得流满下界,我们就让网络的流量为下界。得到一张下界网络。
但是这个下界网络很可能不满足流量守恒(如果守恒,就结束了),所以我们在原图的基础上,令流量上限为 \(Max_e -Min_e\),得到一张增量网络。通过对增量网络的调整,来让下界网络+增量网络达到平衡。

如果在下界网络中,一个点入流大于出流,说明在增量网络中这个点需要补偿出流,出流 > 入流,那么就需要超级源点提供入流来平衡。具体提供的入流是,这个点在下界网络中的出入流量差。(这段话可能有点绕,但还是可以形象理解的)。同理,出流大于入流,向超级汇点连边。
总的来说,差量网络中缺什么,增量网络中补什么,通过源汇点反方向的补偿来达到增量网络平衡。
形式化地讲,设 \(Deg_i=In_i-Out_i\)(下界网络中)。并令 \(Max_e-Min_e\) 为增量网络中每条边的容量。
若 \(Deg_i>0\),则 \(S \rightarrow i\),容量为 \(Deg_i\)。
若 \(Deg_i<0\),则 \(i \rightarrow T\),容量为 \(-Deg_i\)。
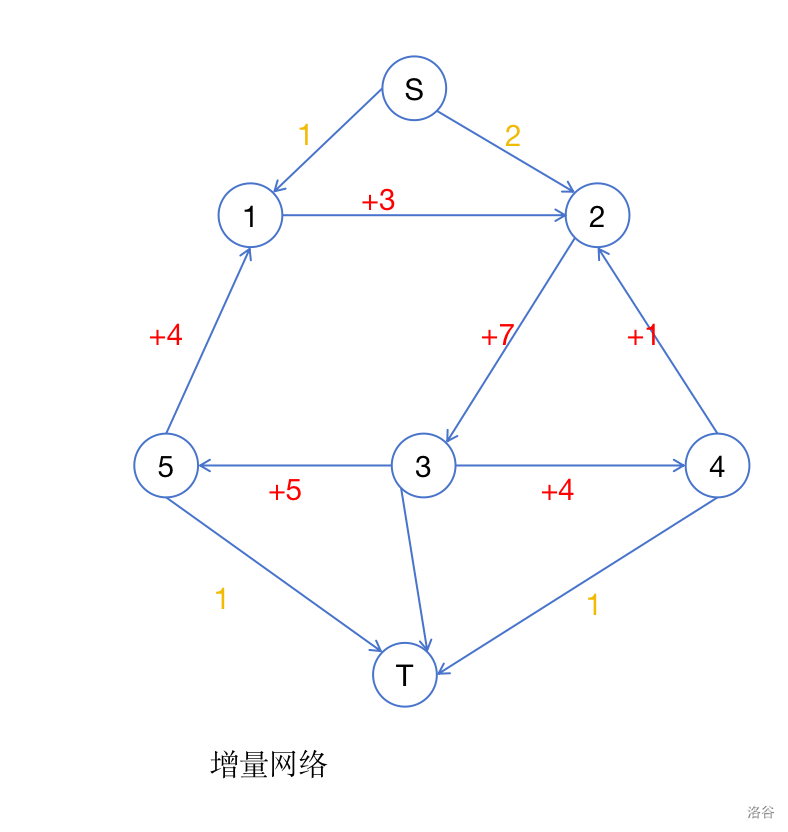
在这样一张增量网络中跑最大流,如果每条新增边(连接超级源汇店的边)达到满流,说明原问题存在可行流,反之不存在。
为什么不求具体流量?为什么没有最大流?因为每一个点流量都不一样啊()。
有源汇上下界可行流
这个就很简单了吧,\(t \rightarrow s\) 连一条 \(INF\) 边,就是上面的问题了。而且我们还能得出可行流的流量是 \(t \rightarrow s\) 边上的流量。
注意这里要分清楚原来的源汇点,和新建的超级源汇点。\(s,t\) 是原网络中的源汇点,\(S,T\) 是为了解决无源汇问题新增的超级源汇点,\(s,t\) 加边后,它们就是普通的结点了。
有源汇上下界最大流
我们先跑出一条可行流,然后撤掉 \(t \rightarrow s\) 的边,以 \(s,t\) 为源汇点,再跑一遍最大流。把可行流和最大流相加。
这个原理也很好理解,计算出可行流后原网络相当于最大流算法里的残量网络,直接在它上面跑就可以。
\(S,T\) 连的边不用撤,因为它们的边已经满流,不会产生影响。
有源汇上下界最小流
这个就很玄学精妙,和最大流一样,只不过从 \(t\) 点开始跑最大流,然后可行流减去最大流。这个操作其实是让原网络的反图达到最大流(还记得网络流中是有反向边的吧)。原图自然最小了。
好了,上下界的网络流基本介绍完了,还有费用流,其实万变不离其宗。
无源汇上下界最小/大费用可行流
是在太帅了这个标题。其实很简单啦,把下界网络中的费用一算,然后在增量网络中跑费用流就行了,注意超级源汇点连的边费用为 \(0\),因为它们的流本质是补偿下界网络,这部分已经算过了。
其他也是一模一样,把所有最大流改成费用流就行了,所以真的很简单啊。(就是模版容易打错)
标签:可行,网络,流量,下界,无源汇,汇点,汇上 From: https://www.cnblogs.com/Uuuuuur/p/18001252