Question

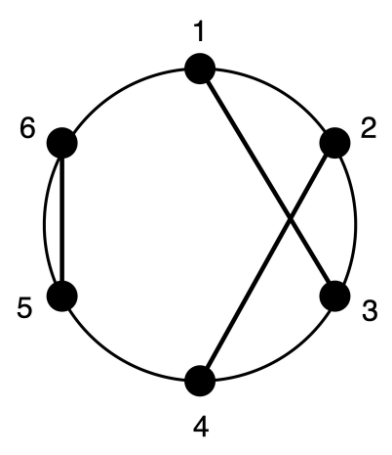
一个圆上有 \(2N\) 个点均匀分布，给出 \(N\) 条线，每条线连接两个顶点

问，有没有两条线相交

Solution

也算一个比较典的题目

考虑到这种两两配对，配对中有没有交错关系的可以考虑异或哈希

因为一个数异或两次等于它本身，所以我们可以用异或来实现一个 “撤销” 操作

我们当我们第二次异或一条线段时，我们只需要判断是否与第一次异或前的值相同即可

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 4e5+5;
int a[maxn],b[maxn],lst[maxn];

int p[maxn],h[maxn];


int main(){
    freopen("E.in","r",stdin);
    srand(time(0));
    
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int x,y; scanf("%d%d",&x,&y);
        if(x>y) swap(x,y); lst[y] = x;
        a[x] = i; a[y] = i;
        b[x] = 1; b[y] = 2;
    }
    for(int i=1;i<=n;i++) h[i] = rand();
    for(int i=1;i<=n;i++) h[i] ^= 2333;

    for(int i=1;i<=2*n;i++){
        if(b[i] == 1){
            p[i] = p[i-1] ^ h[a[i]];
        }
        else{
            p[i] = p[i-1] ^ h[a[i]];
            if(p[i] != p[lst[i]-1]){
                puts("Yes"); return 0;
            }
        }
    }
    puts("No");
    return 0;
}