洛谷题解-P1821 [USACO07FEB] Cow Party S

https://www.luogu.com.cn/problem/P1821

题目描述

寒假到了，nnn 头牛都要去参加一场在编号为 xxx 的牛的农场举行的派对，农场之间有 mmm 条有向路，每条路都有一定的长度。

每头牛参加完派对后都必须回家，无论是去参加派对还是回家，每头牛都会选择最短路径，求这 nnn 头牛的最短路径（一个来回）中最长的一条路径长度。

输入格式

第一行有三个整数，分别表示牛的数量 nnn，道路数 mmm 和派对农场编号 xxx。
接下来 mmm 行，每行三个整数 u,v,wu, v, wu,v,w，表示存在一条由 uuu 通向 vvv 的长度为 www 的道路。

输出格式

输出一行一个整数表示答案。

输入输出样例

4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3

10

说明/提示

样例 1 解释

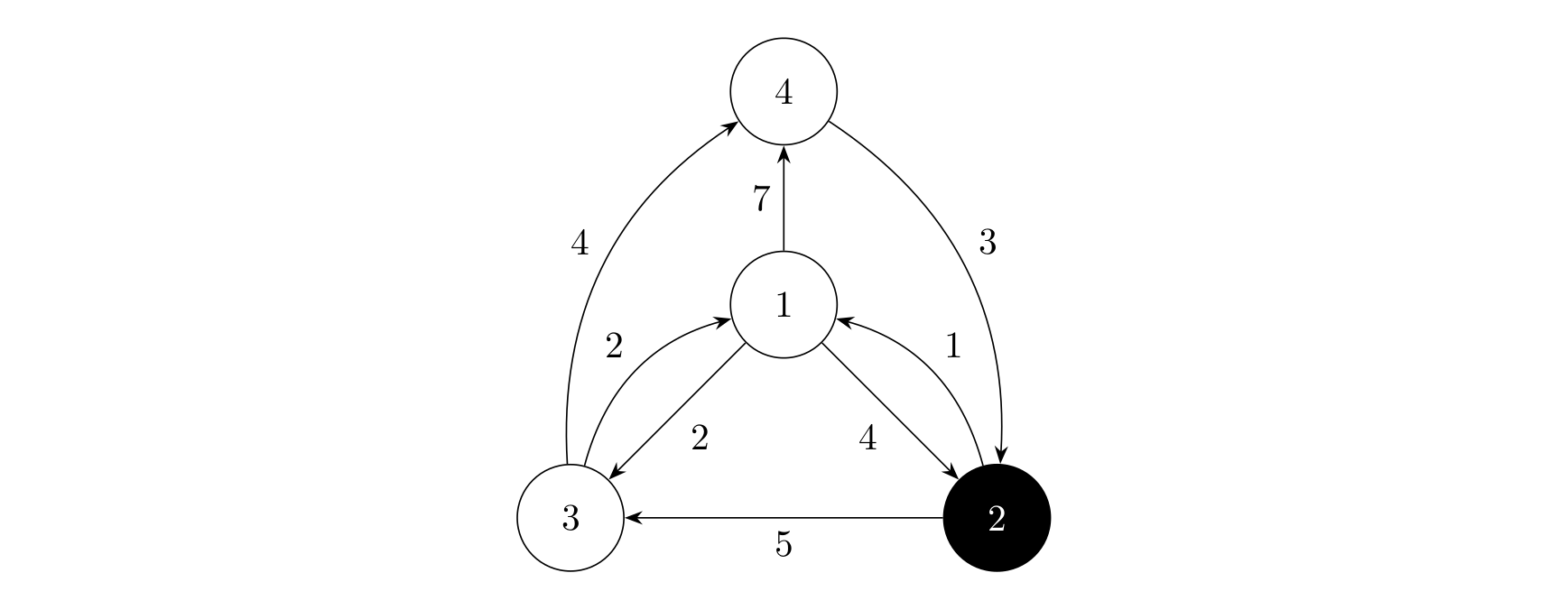
数据规模与约定

对于全部的测试点，保证 1≤x≤n≤1031 \leq x \leq n \leq 10^31≤x≤n≤103，1≤m≤1051 \leq m \leq 10^51≤m≤105，1≤u,v≤n1 \leq u,v \leq n1≤u,v≤n，1≤w≤1021 \leq w \leq 10^21≤w≤102，保证从任何一个结点出发都能到达 xxx 号结点，且从 xxx 出发可以到达其他所有节点。

从1,2,3,4,5..n-1个点到n，可以反向建边，然后从n到1,2,3,...n-1个点；

另外，这题不能瞎*2输出（别只看一个来回），要跑2遍（1...n到x）-> （x到1..n但是反向），（x到1...n但是正向）

#include <bits/stdc++.h>
using namespace std;

const int N=1e5+5;
struct node
{
	int v, w;
	bool operator <(const node &A) const
	{
		return w>A.w;
	}
};
int n, m, x, u1, v1, w1, dis[N], vis[N], dis2[N], ans=0;
vector<node> a[N], a2[N];
priority_queue<node> q;
void dij(int s)
{
	memset(dis, 63, sizeof dis);
	memset(vis, 0, sizeof vis);
	dis[s]=0, q.push({s, 0});
	
	while (!q.empty())
	{
		int u=q.top().v;
		q.pop();
		
		if (vis[u]) continue;
		vis[u]=1;
		
		for (int i=0; i<a[u].size(); i++)
		{
			int v=a[u][i].v, w=a[u][i].w;
			if (!vis[v] && dis[v]>dis[u]+w)
			{
				dis[v]=dis[u]+w;
				q.push({v, dis[v]});
			}
		}
	}
}
void dij2(int s)
{
	memset(dis2, 63, sizeof dis2);
	memset(vis, 0, sizeof vis);
	dis2[s]=0, q.push({s, 0});
	
	while (!q.empty())
	{
		int u=q.top().v;
		q.pop();
		
		if (vis[u]) continue;
		vis[u]=1;
		
		for (int i=0; i<a2[u].size(); i++)
		{
			int v=a2[u][i].v, w=a2[u][i].w;
			if (!vis[v] && dis2[v]>dis2[u]+w)
			{
				dis2[v]=dis2[u]+w;
				q.push({v, dis2[v]});
			}
		}
	}
}
int main()
{
	scanf("%d%d%d", &n, &m, &x);
	for (int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &u1, &v1, &w1);
		a[v1].push_back({u1, w1});
		a2[u1].push_back({v1, w1});
	}
	dij(x);
	dij2(x);
	
	for (int i=1; i<=n; i++) ans=max(ans, dis[i]+dis2[i]);
	printf("%d", ans);
	return 0;
}