首先考虑一个足球场长啥样才是合法的。发现一个点能只拐弯一次到达另一个点,可以分为两种情况:先左右走,再上下走 或 先上下走,后左右走。无论哪种情况,都要求我们走一步使得和目标点一个轴相同,再走一步使得另一个轴也相同,所以加入把每一行选择的格子看成一个区间(因为如果不连续显然是不合法的),我们选择的这些区间一定是互相包含的关系,且必须是一个凸的图形(即不能有工字形)。
然后我们考虑一个 \(O(n^3)\) 的做法,设 \(f(l,r,x)\) 表示考虑第 \([l,r]\) 行,选择的区间一定包含第 \(x\) 列的最大足球场大小(如下图就是一个 \(l=1,r=3,x=1\) 时的例子)。
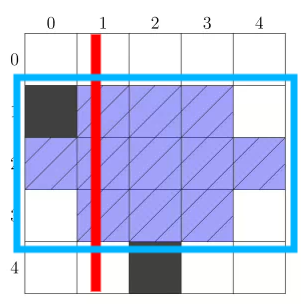
考虑转移。我们对于每个状态 \((l,r,x)\) 维护一个列区间 \([L,R]\),代表我们选择的区间需要为 \([L,R]\) 的子区间,然后从 \((l+1,r,x)\) 与 \((l,r-1,x)\) 转移即可,这个部分是简单的。
但是我们会发现,这样的状态数是 \(O(n^3)\) 的,无法通过这道题。但是我们发现许多状态显然是无用的,如下图。
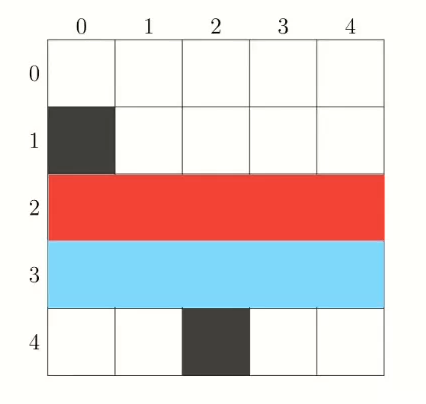
假设我们当前在蓝色状态(即 \((3,3,x)\) 状态),我们发现我们当前的状态一定不能成为答案,因为我们可以没有任何花费的(也就是在保持我们需要选择的区间 \([L,R]\) 不变的情况下)扩展到红色状态+蓝色状态(即 \((2,3,x)\) 状态)。
所以我们发现,我们可以固定 \(r\),有用的整数对 \((l,x)\) 不超过 \(O(n)\) 个(对于每一个 \(x\),我们显然会将 \(l\) 扩展到第 \(x\) 列上最靠下的一个障碍),所以我们只需要 \((r,x)\) 就可以唯一确定一个状态,这样我们的总状态数就降到了 \(O(n^2)\)。
考虑在这种情况下我们怎么进行转移,我们会发现,对于一个状态 \((r,x)\),我们要么就是从 \((r-1,x)\) 增加第 \(r\) 转移来,此时对答案的贡献就是当前这一行能够选择的最大区间长度(即区间 \([\max(L(r,x),L(r-1,x)),\min(R(r,x),R(r-1,x))]\),其中 \(L(r,x)\) 表示状态 \((r,x)\) 能选择的最左边的列,\(R(r,x)\) 以及下文的 \(U(r,x)\) (即向上)同理)。要么就是令第 \(r\) 行为最宽的一行,此时答案为 \(f(r,L(r-1,x))+(U(r,L(r-1,x))-U(r,x)) \times (\min(R(r,x),R(r-1,x))-\max(L(r,x),L(r-1,x)))\)。
最终我们会发现,所有信息的维护都可以在 \(O(1)\) 内完成,时间复杂度 \(O(n^2)\),可以通过本题。
const int MAXN = 2005;
int n, f[MAXN][MAXN], L[MAXN][MAXN], R[MAXN][MAXN], U[MAXN][MAXN], ll[MAXN][MAXN];
vector<pair<int, int>> dp[MAXN];
signed biggest_stadium(signed _, vector<vector<signed>> ___) {
n = _;
vector<vector<int>> a(n + 3, vector<int>(n + 3));
for (int i = n; i >= 1; --i) {
for (int j = n; j >= 1; --j) {
a[i][j] = ___[i - 1][j - 1];
}
}
for (int i = 1; i <= n; ++i)
a[i][0] = a[i][n + 1] = a[0][i] = a[n + 1][i] = 1;
for (int i = 0; i <= n + 1; ++i) {
for (int j = 0; j <= n + 1; ++j) {
if (a[i][j]) U[i][j] = i, L[i][j] = j;
else U[i][j] = U[i - 1][j], L[i][j] = L[i][j - 1];
}
}
for (int i = 0; i <= n + 1; ++i) {
for (int j = n + 1; j >= 0; --j) {
if (a[i][j]) R[i][j] = j;
else R[i][j] = R[i][j + 1];
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (a[i][j]) continue;
dp[i - U[i][j]].push_back({i, j});
ll[i][j] = i - U[i][j];
}
}
int ans = 0;
for (int len = 1; len <= n; ++len) {
for (auto __ : dp[len]) {
int r = __.first, x = __.second;
if (a[r - 1][x]) {
f[r][x] = R[r][x] - L[r][x] - 1;
ans = max(ans, f[r][x]);
continue;
}
f[r][x] = f[r - 1][x] +
(min(R[r - 1][x], R[r][x]) - max(L[r - 1][x], L[r][x]) - 1);
if (L[r - 1][x] > L[r][x]) {
const auto upd = f[r][L[r - 1][x]] +
(U[r][L[r - 1][x]] - U[r][x]) *
(min(R[r - 1][x], R[r][x]) - L[r - 1][x] - 1);
f[r][x] = max(f[r][x], upd);
}
if (R[r - 1][x] < R[r][x]) {
const auto upd = f[r][R[r - 1][x]] +
(U[r][R[r - 1][x]] - U[r][x]) *
(R[r - 1][x] - max(L[r - 1][x], L[r][x]) - 1);
f[r][x] = max(f[r][x], upd);
}
R[r][x] = min(R[r - 1][x], R[r][x]);
L[r][x] = max(L[r - 1][x], L[r][x]);
ans = max(ans, f[r][x]);
}
}
return ans;
}