669.修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
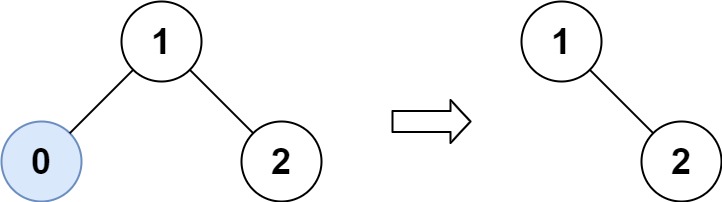
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:
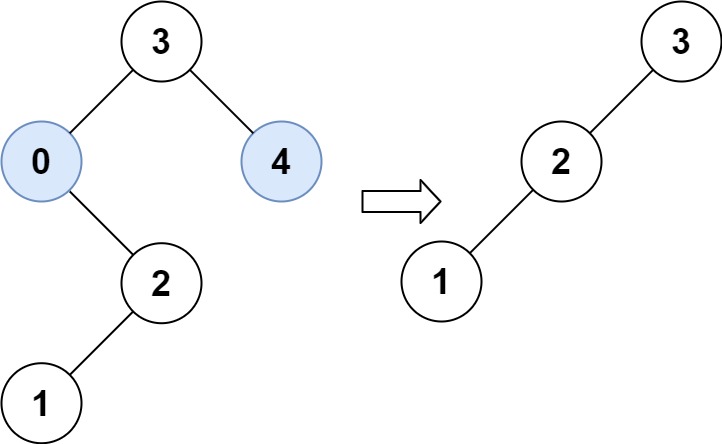
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
递归法
class Solution {
TreeNode left, right;
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) return null;
if (root.val < low) {
left = trimBST(root.right, low, high);// 寻找符合区间[low, high]的节点
return left;
}
if (root.val > high) {
right = trimBST(root.left, low, high);// 寻找符合区间[low, high]的节点
return right;
}
root.left = trimBST(root.left, low, high); // root->left接入符合条件的左孩子
root.right = trimBST(root.right, low, high);// root->right接入符合条件的右孩子
return root;
}
}