[AGC044E] Random Pawn题解
题目链接
AtCoder原题链接
Step 1. 拆环
原问题是在环上的问题,考虑将环拆开变成链来处理。因此,我们需要找到一个点,使得操作越过这个点一定不优。
令使 \(a\) 的值最大的位置的下标为 \(maxp\)。容易发现,如果现在正处在 \(maxp\) 上,那么继续操作一定不可能得到更优的答案。因此,我们可以从 \(maxp\) 的位置将环断开成为一条链。令环上下标为 \(maxp\) 的点在链上的下标为 \(0\),并将环上下标为 \(maxp\) 的点复制一份到链上下标为 \(n\) 的点。操作结束后链上共 \(n + 1\) 个点,下标为 \(0 \sim n\)。(后文中的下标若未加特殊说明则视为链上的下标)
原来在环上的问题被成功转化为在链上的问题。
Step 2. 问题转化
概率和期望问题可用动态规划求解。令 \(dp_i\) 表示以 \(i\) 点为起点的最大期望价值。如果不操作,价值为 \(a_i\);如果操作,价值的期望为 \(\dfrac{f_{i - 1} + f_{i + 1}}{2} - b_i\)。由于每一步要走最优路线,\(f_i\) 为上述两种情况期望价值的最大值。即:
\[f_i = \max\left(a_i,\dfrac{f_{i - 1} + f_{i + 1}}{2}- b_i\right) \]边界条件:\(f_0 = a_0\),\(f_n = a_n\)。
这是一个有后效性的动态规划,因此考虑解方程组,\(f_i\) 为未知数,\(a_i\),\(b_i\) 为参数。
Step 3. 消去常数
方程组里的的常数项 \(b_i\) 很烦人,考虑消去 \(b_i\) 。由于 \(\max\) 函数左半部分为常数,右半部分与 \(f\) 相关,比较常见的做法是构造一个数组 \(d\) 并令 \(g_i = f_i + d_i\),将与 \(f\) 相关的方程组转换为与 \(g\) 有关的方程组,从而消去 \(\max\) 右半部分的常数。具体而言:
\[g_i = f_i + d_i \]\[g_i = \max\left(a_i + d_i,\dfrac{f_{i - 1} + f_{i + 1}}{2}- b_i + d_i\right) \]\[g_i = \max\left(a_i + d_i,\dfrac{g_{i - 1} - d_{i - 1} + g_{i + 1} - d_{i + 1}}{2}- b_i + d_i\right) \]\[g_i = \max\left(a_i + d_i,\dfrac{g_{i - 1}+ g_{i + 1} }{2}- \dfrac{ d_{i - 1} + d_{i + 1}}{2}- b_i + d_i\right) \]我们要消去常数,因此我们令 $ - \dfrac{ d_{i - 1} + d_{i + 1}}{2}- b_i + d_i = 0 $。于是我们得到的 \(d\) 的递推式:
\[d_{i + 1} = 2\left(d_i - b_i\right) - d_i \]由于 \(d\) 的作用只是消去常数,我们并不关心 \(d\) 取什么值,满足递推关系即可。因此 \(d_0\) 和 \(d_1\) 可以随便取(例如都取 \(0\))。
方程式化简为:
令 \(c_i = a_i + d_i\),最终方程组为:
\[g_i = \max\left(c_i,\dfrac{g_{i - 1}+ g_{i + 1} }{2}\right) \]边界条件:\(g_0 = c_0\),\(g_n = c_n\)。
原问题被转化为一个方程组的求解。
Step 4. 方程组求解
观察到 \(\dfrac{g_{i - 1}+ g_{i + 1} }{2}\) 的结构类似中点公式。于是考虑将问题放到平面直角坐标系上。在坐标系内点 \(n + 1\) 个点, 每个点的坐标为 \(\left( i, g_i \right)\)。
假设不考虑 \(c_i\) 的限制,那么中间每个点均为左右两边的点的连线段的中点,每个点都在左右两边的点的连线段上。此时所有点都在一条线段上。
那么这些点的排布可能如下:(\(g_0, g_n\) 随便取的)
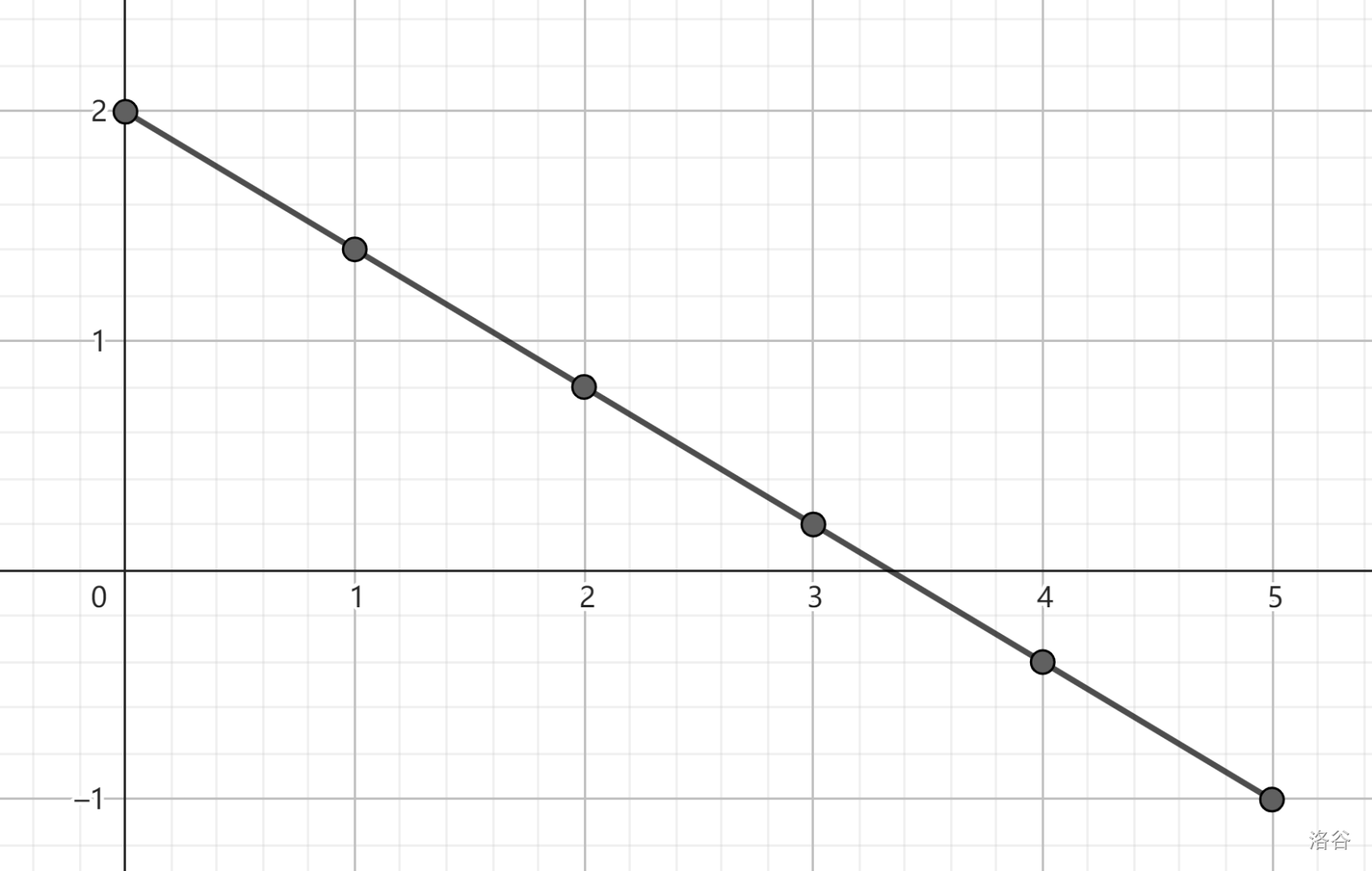
接下来考虑带上 \(c_i\) 的情况。
我们分析 \(c_i\) 对解的影响。如果 \(c_i\) 小于或等于原来的 \(g_i\),那么 \(c_i\) 不会产生影响;如果 \(c_i\) 大于原来的 \(g_i\),那么 \(g_i\) 就会被增大为 \(c_i\),其他点也会随 \(g_i\) 的变化而变化。可以理解为 \(c_i\) 把这个点“顶”起来了。如图所示:
带上 \(c_2\):
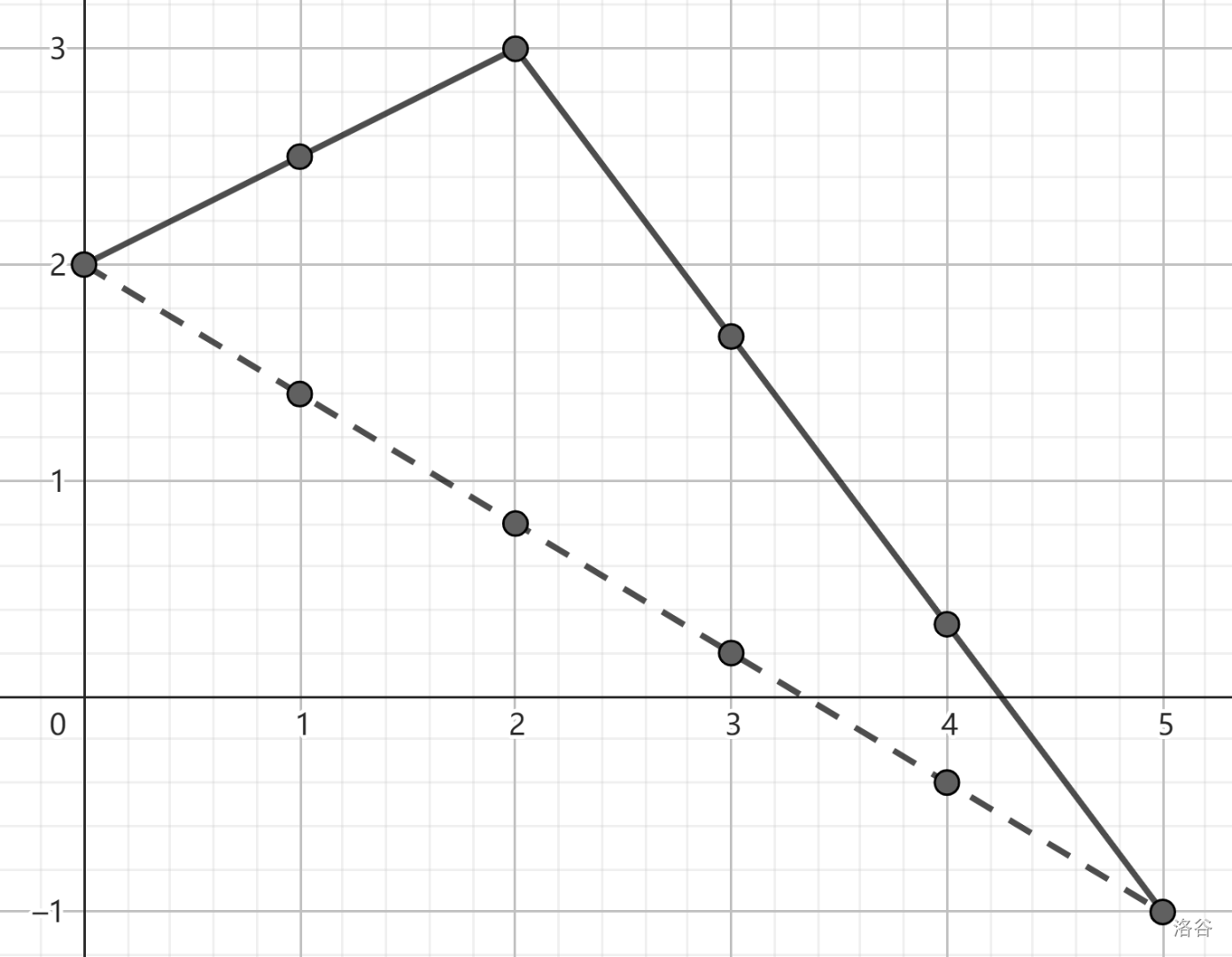
再带上 \(c_4\):
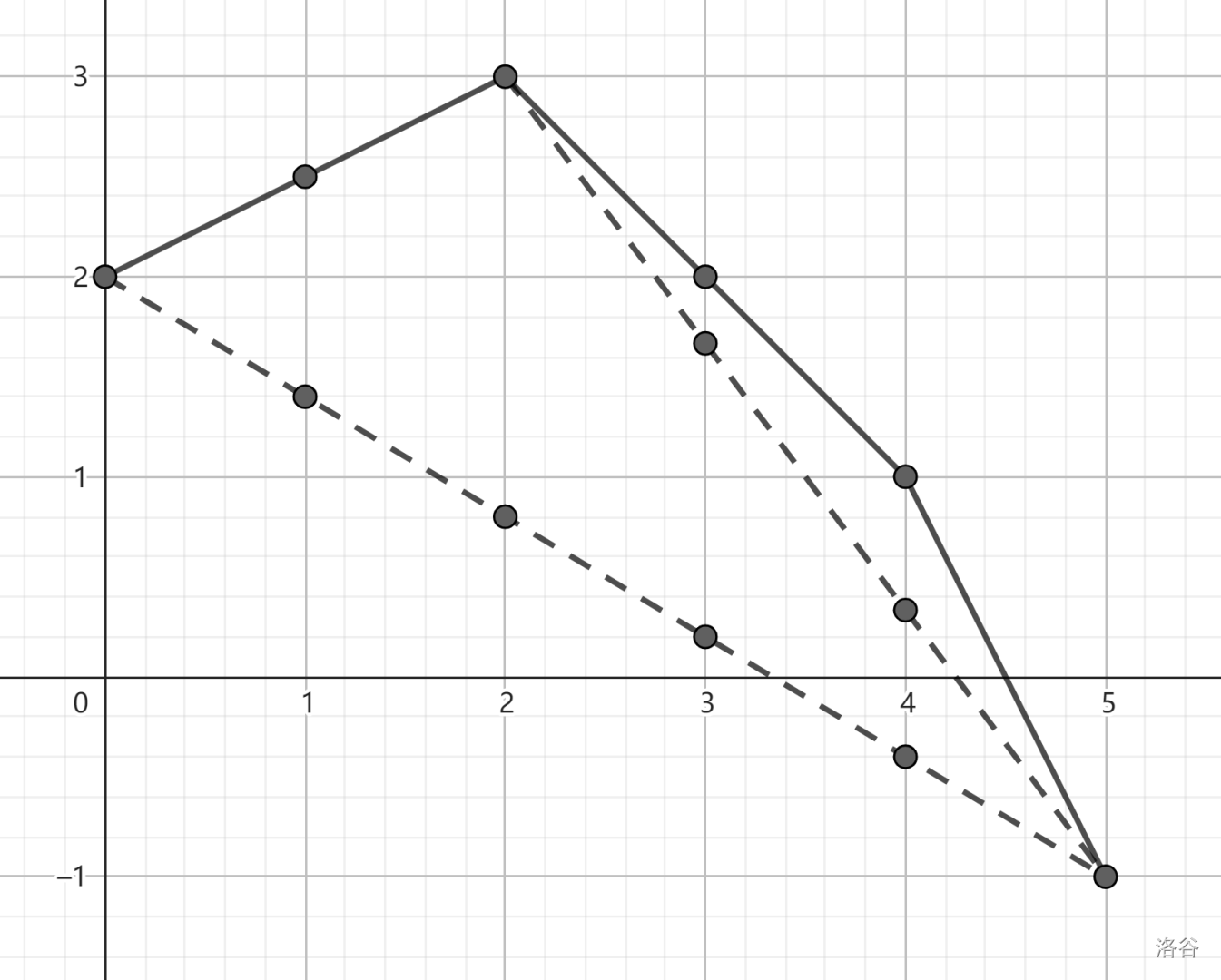
容易发现,经过若干次操作后,线段和点形成了一个上凸壳,即线段的斜率单调递减。
为什么是一个上凸壳?因为 \(\max\) 函数和 \(\dfrac{g_{i - 1}+ g_{i + 1} }{2}\) 的结构保证了一个点的位置不会比三点共线时低。严谨证明较为简单,请读者自证。
可以理解为:\(c_i\) 规定了每个点位置的理想值,而 \(\max\) 函数和 \(\dfrac{g_{i - 1}+ g_{i + 1} }{2}\) 的结构保证了图形的凹凸性。
原问题转化为对给定的若干点求上凸壳。
\(\left(0, c_0\right)\) 和 \(\left(n, c_n\right)\) 已经确定,使用单调栈维护凸壳上斜率递减的线段即可。
得到上凸壳之后,我们计算出 \(g_i\) 并还原出 \(f_i\) 就能够得到从每个点出发价值的期望,对 $i \in \left [1, n \right ] $ 求出 \(f_i\) 的平均值即为答案。
时间复杂度为 \(O\left(n\right)\)。
总结
本题的原问题经历了三次转化:
-
将环断开为链,把环上问题变为链上问题。
-
利用动态规划,将最优策略问题变为有后效性动态规划解方程组问题,并将每个未知数加上一个常数来消常数。
-
把未知数放到平面直角坐标系上,观察出上凸壳性质,将解方程组问题转化为上凸壳维护的问题。
环拆链和有后效性动态规划的转化比较常见,但消去常数和维护上凸壳的转化较为巧妙,而消去常数的一大原因是找到了大致的上凸壳关系。因此,找到上凸壳的性质是解出本题的关键。
在平时做题的时候,要多多注意积累类似的转化。同时,任何题目的关系式都一定不是空穴来风,要注意观察,构造几何模型,更好地发掘性质,以求问题的简单化。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 200010;
int n, maxp;
double a[MAXN], b[MAXN], f[MAXN], g[MAXN], d[MAXN], c[MAXN];
double ans;
int q[MAXN];
int tot;
bool Cmpk(const int i){
double k1 = (c[i] - c[q[tot]]) / (i - q[tot]);
double k2 = (c[q[tot]] - c[q[tot - 1]]) / (q[tot] - q[tot - 1]);
return k1 > k2;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i){
scanf("%lf", a + i);
if (a[i] > a[maxp]) maxp = i;
}
for (int i = 0; i < n; ++i) scanf("%lf", b + i);
double tmp[MAXN];
for (int i = 0; i < n; ++i) tmp[i] = a[(i + maxp) % n];
for (int i = 0; i < n; ++i) a[i] = tmp[i];
for (int i = 0; i < n; ++i) tmp[i] = b[(i + maxp) % n];
for (int i = 0; i < n; ++i) b[i] = tmp[i];
a[n] = a[0];
for (int i = 1; i < n; ++i) d[i + 1] = (d[i] - b[i]) * 2 - d[i - 1];
for (int i = 0; i <= n; ++i) c[i] = a[i] + d[i];
q[0] = 0;
for (int i = 1; i <= n; ++i) {
while (tot && Cmpk(i)) --tot;
q[++tot] = i;
}
//q为单调栈,维护凸包内线段端点的点集
for (int i = 0; i < tot; ++i) {
double know = (c[q[i + 1]] - c[q[i]]) / (q[i + 1] - q[i]);
double bnow = c[q[i]] - know * q[i];
for (int j = q[i]; j < q[i + 1]; ++j) {
g[j] = know * j + bnow;
}
}
for (int i = 0; i < n; ++i) f[i] = g[i] - d[i], ans += f[i];
ans /= n;
printf("%.12lf\n", ans);
return 0;
}