看看会不会咕/cf
除非极度不可做题,否则一般都是会写的。
每个题限时思考 \(30\min\),如果有想法可以延长;然后自己写/看题解。
BJOI2019
P5322 排兵布阵
- \(\color{blue}\texttt{以前做过}\)
比较水的,略。
P5323 光线
- \(\color{blue}\texttt{以前做过}\)
考虑记 \(f_i\) 为直接穿过第 \(i\) 面镜子的光有多少,记 \(g_i\) 为从第 \(i\) 面镜子反射回来的光有多少。
易得:
\[\begin{aligned} f_i & = f_{i-1}a_i\sum\limits_{k=0}^{\infty} (g_{i-1}b_i)^k\\ g_i & = b_i+g_{i-1}a_i^2\sum\limits_{k=0}^{\infty} (g_{i-1}b_i)^k \end{aligned} \]核心思想是一道光从上面打下了和从下面打上来,一面镜子能射回去的光是相同的。
然后就做完了。
P5324 删数
- \(\color{gold}\texttt{想出 50\% 以上}\)
主要是之前做过其弱化版 AGC17C,所以一上来就有想法。
首先观察到的是,这个题和 AGC17C 唯一的区别就是多了全局 \(\pm 1\) 的操作,所以很自然的会去想到维护一个 \(\Delta\) 去描述这个东西。
然后 update 操作就变成了 delete 掉 \(a_p\) 再 insert 进去 \(x+\Delta\),然后最后就是查询 \(n-\text{sum of }(1+\Delta,n+\Delta)\) 的值。
看起来很对,但是有一种特殊情况:
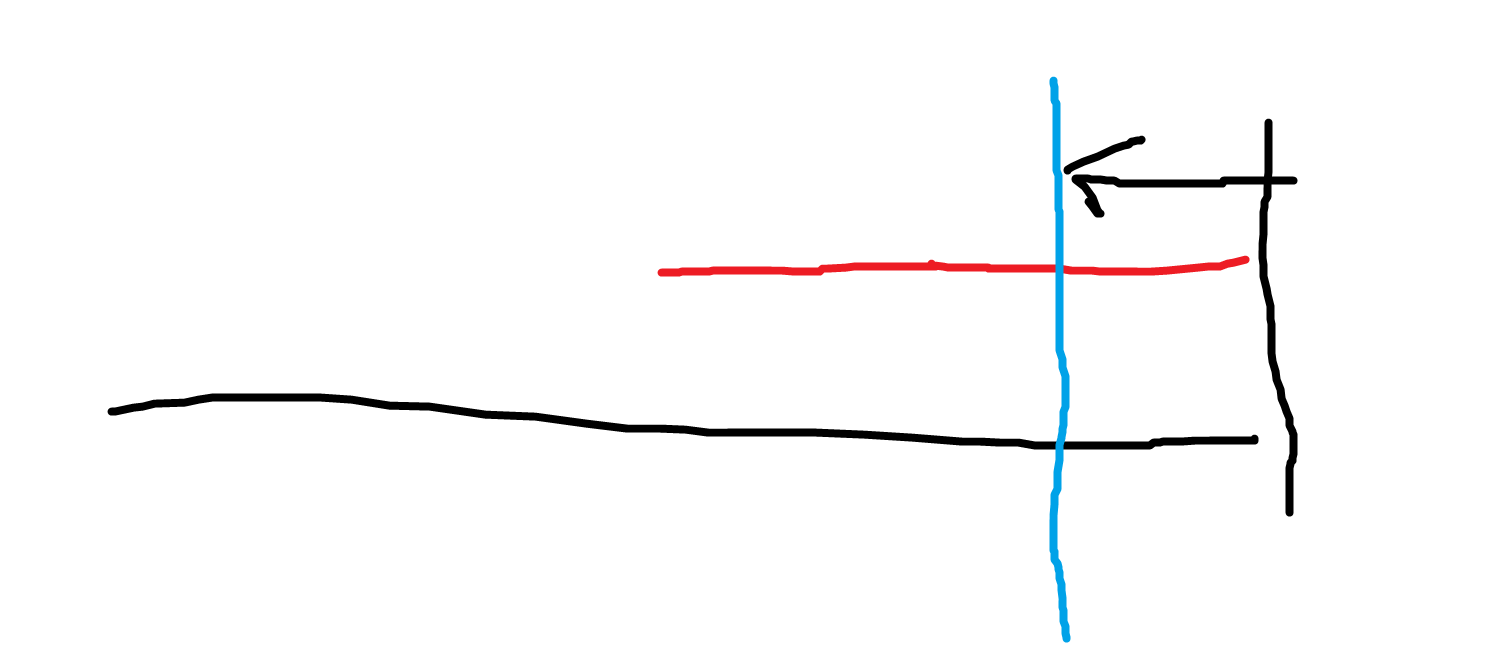
如图,我们的合法区间边界 \([1+\Delta,n+\Delta]\) 向左挪了一点(黑->蓝),然后红线(对应一条线段 \((x-cnt_x+1)\text{-}(x)\))的端点到了边框之外,这时候显然整个红线我们都要 change 掉(因为不满足 \(a_i=n\) 了),但是事实上根据我们上面的做法还是会将其统计进去。
所以我们上面讲了一堆是个假做法。
考虑如何处理,一个比较自然的想法是,每次边框左移时,就把红线 delete 掉;右移时再把红线 insert 进去。
那么这个相对于要支持下面的一个数据结构:
- 区间修,不会出现负数,查询一个区间内有多少个 \(0\)。
考虑到如果一个区间内出现了零,则其必然时整个区间的最小值(因为值非负),所以我们维护一个区间的最小值和最小值出现个数即可,这个是简单的。
然后就做完了,复杂度 \(\Theta((n+q)\log{n})\)。
标签:选题,板刷,sum,texttt,AGC17C,color,2019,Delta,区间 From: https://www.cnblogs.com/lsj2009/p/17961683