返回 C 组做题,然后发现自己挂分了。
T1 寻找道路
[NOIP2014 提高组] 寻找道路
题目背景
NOIP2014 提高组 D2T2
题目描述
在有向图 \(G\) 中,每条边的长度均为 \(1\),现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
- 路径上的所有点的出边所指向的点都直接或间接与终点连通。
- 在满足条件 \(1\) 的情况下使路径最短。
注意:图 \(G\) 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入格式
第一行有两个用一个空格隔开的整数 \(n\) 和 \(m\),表示图有 \(n\) 个点和 \(m\) 条边。
接下来的 \(m\) 行每行 \(2\) 个整数 \(x,y\),之间用一个空格隔开,表示有一条边从点 \(x\) 指向点 \(y\)。
最后一行有两个用一个空格隔开的整数 \(s,t\),表示起点为 \(s\),终点为 \(t\)。
输出格式
输出只有一行,包含一个整数,表示满足题目描述的最短路径的长度。如果这样的路径不存在,输出 \(-1\)。
样例 #1
样例输入 #1
3 2 1 2 2 1 1 3样例输出 #1
-1样例 #2
样例输入 #2
6 6 1 2 1 3 2 6 2 5 4 5 3 4 1 5样例输出 #2
3提示
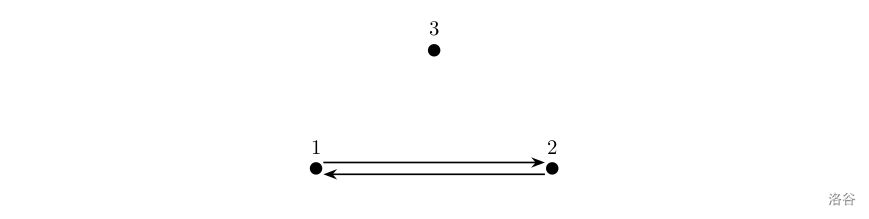
样例 1 解释
如上图所示,箭头表示有向道路,圆点表示城市。起点 \(1\) 与终点 \(3\) 不连通,所以满足题目描述的路径不存在,故输出 \(-1\)。
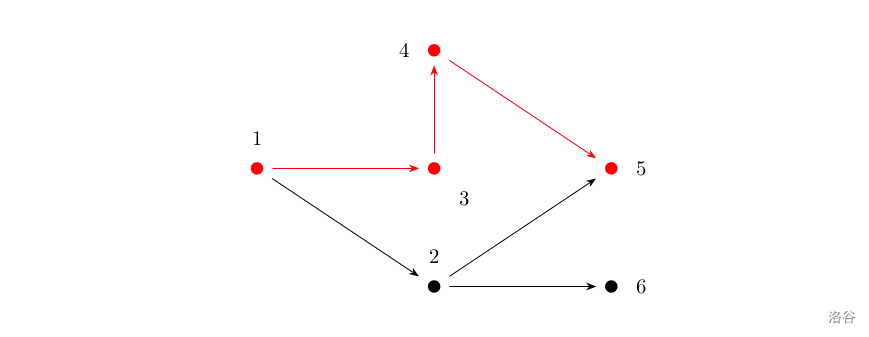
样例 2 解释
如上图所示,满足条件的路径为 \(1\to 3\to 4\to 5\)。注意点 \(2\) 不能在答案路径中,因为点 \(2\) 连了一条边到点 \(6\),而点 \(6\) 不与终点 \(5\) 连通。数据范围及约定
- 对于 \(30\%\) 的数据,\(0<n\le10\),\(0<m\le 20\)。
- 对于 \(60\%\) 的数据,\(0<n\le100\),\(0<m\le 2000\)。
- 对于 \(100\%\) 的数据,\(0<n\le 10^4\),\(0<m\le 2\times 10^5\),\(0<x,y,s,t\le n,x,s\ne t\)。
反向建边,跑 dfs 算出能到达终点的点,然后跑 dij 就可以了。
/**
* @file 寻找道路.cpp
* @tag: #GMOJ#最短路
* @author: ZnPdCo
* @date: 2023-12-30 14:26:11
* @problem: https://gmoj.net/senior/#main/show/3934
**/
#include <cstdio>
#include <queue>
#define ll long long
#define N 10010
#define M 200010
using namespace std;
ll n, m, st, ed;
bool flag[N], go[N];
ll head[N];
ll nxt[2*M];
bool type[2*M];
ll to[2*M], cnt;
void addEdge(ll u, ll v, ll t) {
cnt++;
to[cnt] = v;
nxt[cnt] = head[u];
type[cnt] = t;
head[u] = cnt;
}
void dfs(ll u) {
flag[u] = 1;
for(ll i = head[u]; i; i = nxt[i]) if(type[i] == 1) {
ll v = to[i];
if(!flag[v]) dfs(v);
}
}
priority_queue<pair<ll, ll> > q;
ll dis[N];
bool vis[N];
void dij() {
for(ll i = 1; i <= n; i++) dis[i] = 1e15;
dis[st] = 0;
q.push(make_pair(0, st));
while(!q.empty()) {
ll u = q.top().second;
q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(ll i = head[u]; i; i = nxt[i]) if(type[i] == 0) {
ll v = to[i];
if(!go[v]) continue;
if(!vis[v]) {
if(dis[v] > dis[u] + 1) {
dis[v] = dis[u] + 1;
q.push(make_pair(-dis[v], v));
}
}
}
}
}
int main() {
scanf("%lld %lld", &n, &m);
for(ll i = 1; i <= m; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
addEdge(u, v, 0);
addEdge(v, u, 1);
}
scanf("%lld %lld", &st, &ed);
dfs(ed);
for(ll u = 1; u <= n; u++) {
go[u] = true;
for(ll i = head[u]; i; i = nxt[i]) {
ll v = to[i];
if(flag[v] == 0) go[u] = false;
}
}
dij();
if(dis[ed] == 1e15) printf("-1");
else printf("%lld", dis[ed]);
}
/*
3 3
1 2
2 3
3 1
1 2
*/
T2 联合权值
[NOIP2014 提高组] 联合权值
题目背景
NOIP2014 提高组 D1T2
题目描述
无向连通图 \(G\) 有 \(n\) 个点,\(n-1\) 条边。点从 \(1\) 到 \(n\) 依次编号,编号为 \(i\) 的点的权值为 \(W_i\),每条边的长度均为 \(1\)。图上两点 \((u, v)\) 的距离定义为 \(u\) 点到 \(v\) 点的最短距离。对于图 \(G\) 上的点对 \((u, v)\),若它们的距离为 \(2\),则它们之间会产生 \(W_v \times W_u\) 的联合权值。
请问图 \(G\) 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入格式
第一行包含 \(1\) 个整数 \(n\)。
接下来 \(n-1\) 行,每行包含 \(2\) 个用空格隔开的正整数 \(u,v\),表示编号为 \(u\) 和编号为 \(v\) 的点之间有边相连。
最后 \(1\) 行,包含 \(n\) 个正整数,每两个正整数之间用一个空格隔开,其中第 \(i\) 个整数表示图 \(G\) 上编号为 \(i\) 的点的权值为 \(W_i\)。
输出格式
输出共 \(1\) 行,包含 \(2\) 个整数,之间用一个空格隔开,依次为图 \(G\) 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对 \(10007\) 取余。
样例 #1
样例输入 #1
5 1 2 2 3 3 4 4 5 1 5 2 3 10样例输出 #1
20 74提示
样例解释
本例输入的图如上所示,距离为 \(2\) 的有序点对有\((1,3)\) 、\((2,4)\) 、\((3,1)\) 、$(3,5) \(、\)(4,2)$ 、$(5,3) $。
其联合权值分别为 \(2,15,2,20,15,20\)。其中最大的是 \(20\),总和为 \(74\)。
数据说明
- 对于 \(30\%\) 的数据,\(1 < n \leq 100\);
- 对于 \(60\%\) 的数据,\(1 < n \leq 2000\);
- 对于 \(100\%\) 的数据,\(1 < n \leq 2\times 10^5\),\(0 < W_i \leq 10000\)。
保证一定存在可产生联合权值的有序点对。
样例太水了,脑子也抽了,忘记还有兄弟距离了。
题目说得很明白,就是一棵树。对于树上的每一个节点与其相连的两个不同节点距离为 2。
然后就是数学题了。
/**
* @file 联合权值.cpp
* @tag: #GMOJ#树
* @author: ZnPdCo
* @date: 2023-12-30 14:26:53
* @problem: https://gmoj.net/senior/#main/show/3931
**/
#include <cstdio>
#include <algorithm>
#define ll long long
#define N 200010
#define P 10007
using namespace std;
ll n, w[N], ans1, ans2;
ll fa[N];
ll dep[N];
ll f[N], mx[N];
ll head[N];
ll nxt[2*N];
ll to[2*N], cnt;
void addEdge(ll u, ll v) {
cnt++;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
int main() {
scanf("%lld", &n);
for(ll i = 1; i < n; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
for(ll i = 1; i <= n; i++) {
scanf("%lld", &w[i]);
}
for(ll u = 1; u <= n; u++) {
ll sum1 = 0, sum2 = 0, mx1 = 0, mx2 = 0;
for(ll j = head[u]; j; j = nxt[j]) {
ll v = to[j];
(sum1 += w[v]) %= P;
(sum2 += w[v]*w[v]) %= P;
if(w[v] > mx1) mx1 = w[v];
else if(w[v] > mx2) mx2 = w[v];
}
ans1 = max(ans1, mx1*mx2);
(ans2 += sum1 * sum1 - sum2) %= P;
}
printf("%lld %lld", ans1, ans2);
}
T3 飞扬的小鸟
[NOIP2014 提高组] 飞扬的小鸟
题目背景
NOIP2014 提高组 D1T3
题目描述
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为 \(n\),高为 \(m\) 的二维平面,其中有 \(k\) 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 \(1\),竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 \(x\),每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 \(y\)。小鸟位于横坐标方向不同位置时,上升的高度 \(x\) 和下降的高度 \(y\) 可能互不相同。
小鸟高度等于 \(0\) 或者小鸟碰到管道时,游戏失败。小鸟高度为 \(m\) 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
输入格式
第 \(1\) 行有 \(3\) 个整数 \(n, m, k\),分别表示游戏界面的长度,高度和水管的数量,每两个整数之间用一个空格隔开;
接下来的 \(n\) 行,每行 \(2\) 个用一个空格隔开的整数 \(x\) 和 \(y\),依次表示在横坐标位置 \(0 \sim n-1\) 上玩家点击屏幕后,小鸟在下一位置上升的高度 \(x\),以及在这个位置上玩家不点击屏幕时,小鸟在下一位置下降的高度 \(y\)。
接下来 \(k\) 行,每行 \(3\) 个整数 \(p,l,h\),每两个整数之间用一个空格隔开。每行表示一个管道,其中 \(p\) 表示管道的横坐标,\(l\) 表示此管道缝隙的下边沿高度,\(h\) 表示管道缝隙上边沿的高度(输入数据保证 \(p\) 各不相同,但不保证按照大小顺序给出)。
输出格式
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出 \(1\),否则输出 \(0\)。
第二行,包含一个整数,如果第一行为 \(1\),则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
样例 #1
样例输入 #1
10 10 6 3 9 9 9 1 2 1 3 1 2 1 1 2 1 2 1 1 6 2 2 1 2 7 5 1 5 6 3 5 7 5 8 8 7 9 9 1 3样例输出 #1
1 6样例 #2
样例输入 #2
10 10 4 1 2 3 1 2 2 1 8 1 8 3 2 2 1 2 1 2 2 1 2 1 0 2 6 7 9 9 1 4 3 8 10样例输出 #2
0 3提示
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
【数据范围】
对于 \(30\%\) 的数据:\(5 \leq n \leq 10, 5 \leq m \leq 10, k=0\),保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\) 次;
对于 \(50\%\) 的数据:\(5 \leq n \leq 20, 5 \leq m \leq 10\),保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\) 次;
对于 \(70\%\) 的数据:\(5 \leq n \leq 1000, 5 \leq m \leq 100\);
对于 \(100\%\) 的数据:\(5 \leq n \leq 10000\),\(5 \leq m \leq 1000\),\(0 \leq k < n\),\(0 < x,y < m\),\(0 < p < n\),\(0 \leq l < h \leq m\), \(l + 1 < h\)。
赛时不知道为什么,直接上线段树,常数炸了。
其实可以直接用背包思想。原题就是一个可重复取的背包。
/**
* @file 飞扬的小鸟.cpp
* @tag: #GMOJ#dp
* @author: ZnPdCo
* @date: 2023-12-30 14:27:53
* @problem: https://gmoj.net/senior/#main/show/3932
**/
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define N 10010
using namespace std;
ll n, m, k, ans2;
ll x[N], y[N];
ll f[2][N];
struct node {
ll p, h, l;
} a[N];
ll pos = 1;
bool cmp(node x, node y) {
return x.p < y.p;
}
int main() {
scanf("%lld %lld %lld", &n, &m, &k);
for(ll i = 1; i <= n; i++) {
scanf("%lld %lld", &x[i], &y[i]);
}
for(ll i = 1; i <= k; i++) {
scanf("%lld %lld %lld", &a[i].p, &a[i].l, &a[i].h);
}
sort(a+1, a+1+k, cmp);
for(ll i = 1; i <= n; i++) {
for(ll j = 0; j <= m; j++) f[i%2][j] = 1e15;
for(ll j = x[i]+1; j < m; j++) {
f[i%2][j] = min(f[i%2][j], min(f[(i-1)%2][j-x[i]], f[i%2][j-x[i]]) + 1);
}
for(ll j = m - x[i]; j <= m; j++) {
f[i%2][m] = min(f[i%2][m], min(f[(i-1)%2][j], f[i%2][j]) + 1);
}
for(ll j = 0; j <= m - y[i]; j++) {
f[i%2][j] = min(f[i%2][j], f[(i-1)%2][j+y[i]]);
}
// for(ll j = 0; j <= m; j++) printf("f[%lld][%lld]=%lld\n", i, j, f[i%2][j]);
if(pos <= k && a[pos].p == i) {
for(ll j = 0; j <= a[pos].l; j++) f[i%2][j] = 1e15;
for(ll j = a[pos].h; j <= m; j++) f[i%2][j] = 1e15;
for(ll j = 0; j <= m; j++) {
if(f[i%2][j] != 1e15) {
ans2 = max(ans2, pos);
}
}
pos++;
}
}
ll ans = 1e15;
for(ll i = 1; i <= m; i++) {
ans = min(ans, f[n%2][i]);
}
if(ans != 1e15) {
printf("1\n");
printf("%lld", ans);
} else {
printf("0\n");
printf("%lld", ans2);
}
}
T4 解方程
[NOIP2014 提高组] 解方程
题目背景
NOIP2014 提高组 D2T3
题目描述
已知多项式方程:
\[a_0+a_1x+a_2x^2+\cdots+a_nx^n=0 \]求这个方程在 \([1,m]\) 内的整数解(\(n\) 和 \(m\) 均为正整数)。
输入格式
输入共 \(n + 2\) 行。
第一行包含 \(2\) 个整数 \(n, m\) ,每两个整数之间用一个空格隔开。
接下来的 \(n+1\) 行每行包含一个整数,依次为 \(a_0,a_1,a_2\ldots a_n\) 。
输出格式
第一行输出方程在 \([1,m]\) 内的整数解的个数。
接下来每行一个整数,按照从小到大的顺序依次输出方程在 \([1,m]\) 内的一个整数解。
样例 #1
样例输入 #1
2 10 1 -2 1样例输出 #1
1 1样例 #2
样例输入 #2
2 10 2 -3 1样例输出 #2
2 1 2样例 #3
样例输入 #3
2 10 1 3 2样例输出 #3
0提示
对于 \(30\%\) 的数据:\(0<n\le 2,|a_i|\le 100,a_n≠0,m<100\) 。
对于 \(50\%\) 的数据:\(0<n\le 100,|a_i|\le 10^{100},a_n≠0,m<100\) 。
对于 \(70\%\) 的数据:\(0<n\le 100,|a_i|\le 10^{10000},a_n≠0,m<10^4\) 。
对于 \(100\%\) 的数据:\(0<n\le 100,|a_i|\le 10^{10000},a_n≠0,m<10^6\) 。
赛时一眼 \(O(nm)\) 正解,然后不知道为什么我竟然每次都求一次 \(x^i\),常数送到 30pts。
因为 \(0\bmod p = 0\),我们可以利用模数的性质,把 \(a_i\) 都取模,然后就是正常暴力。
但是对于 \(p\) 的倍数怎么办呢?没关系,两个模数撞的概率比较小,就可以过了。
我只用了 \(998244353\)。
不要每次都求一次 \(x^i\)。
然后可以边输入边取模。
/**
* @file 联合权值.cpp
* @tag: #GMOJ#玄学
* @author: ZnPdCo
* @date: 2023-12-30 14:27:22
* @problem: https://gmoj.net/senior/#main/show/3935
**/
#include <cstdio>
#include <random>
#include <ctime>
#include <algorithm>
using namespace std;
#define ll long long
#define N 110
#define P 998244353
mt19937 rnd(time(0));
ll n, m;
ll a[N];
bool ismx;
ll ans[N], cnt;
ll read() {
ll x=0, flag = 0;
char c = '.';
while((c < '0' || c > '9') && c != '-') c = getchar();
if(c == '-') flag = 1, c = getchar();
while(c >= '0' && c <= '9') {
x = ((x<<1)%P + (x<<3)%P + (c^'0')) % P;
c = getchar();
}
if(flag) x = (-x % P + P) % P;
return x;
}
void output() {
printf("%lld\n", cnt);
for(ll i = 1; i <= cnt; i++) {
printf("%lld\n", ans[i]);
}
}
int main() {
n = read(), m = read();
for(ll i = 0; i <= n; i++) {
a[i] = read();
}
for(ll i = 1; i <= m; i++) {
ll sum = 0, xc = 1;
for(ll j = 0; j <= n; j++) {
(sum += a[j] * xc % P) %= P;
(xc *= i) %= P;
}
if(sum == 0) ans[++cnt] = i;
}
output();
}
比赛赛时发挥不好,很多点都没有想到,特别是 T3,完全没有把背包联系起来(最后其实想到了,但不知道为什么自己丢掉了)
标签:输出,12,权值,ll,30,样例,小鸟,leq,2023 From: https://www.cnblogs.com/znpdco/p/17936339.html