题目描述
有一天,小 D 在刷朋友圈时看到了一段游戏视频。
这个游戏的名字叫涂色游戏,视频中的游戏界面是一个 \(n\) 行 \(m\) 列的网格,初始时每一个格子都是白色(用数字 \(0\) 表示)。其中每一行的左侧、每一列的上方都有一把带颜色的刷子。玩家点击某个刷子后,这个刷子会将其右侧(或下方)的一整行(或一整列)涂上同一种颜色,该行(或该列)格子原有的颜色都会被覆盖成新涂上的颜色。
下图展示的情况可以通过先将第一列涂成红色,然后将第一行涂成蓝色得到,若此时选择将第三列涂成绿色,则图中绿色方框中的格子都会变成绿色。
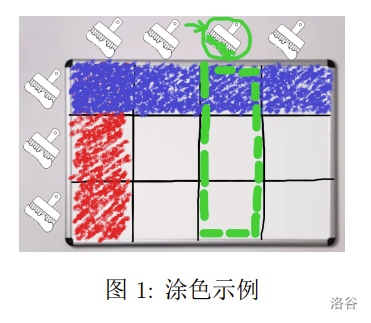
小 D 想用他自己编写的程序来进行视频中的游戏。在编程的过程中,小 D 在涂色逻辑的实现上却遇到了一些困难,于是他向你求助,希望你能帮他完成实现涂色逻辑部分的代码。
首先,小 D 会给你网格的行数和列数 \(n, m\),然后给出 \(q\) 次操作,每次操作用三个整数 \(opt_i, x_i, c_i\) 表示:
- 如果 \(opt_i=0\),那么这次操作会将第 \(x_i\) 行涂成颜色 \(c_i\)。
- 如果 \(opt_i=1\),那么这次操作会将第 \(x_i\) 列涂成颜色 \(c_i\)。
在所有涂色操作结束以后,你需要输出网格中每个位置的颜色是什么。
输入格式
本题有多组测试数据。
第一行包含一个正整数 \(T\),表示数据组数。
接下来一共 \(T\) 组数据,每组数据格式如下:
第一行包含三个整数 \(n, m, q\),分别表示涂色板的行数、列数,以及小 D 进行涂色操作的次数。
接下来 \(q\) 行,每行包含三个整数 \(opt_i, x_i, c_i\),表示一次操作。
输出格式
对于每组数据,输出 \(n\) 行,每行 \(m\) 个由单个空格隔开的整数。
其中第 \(i\) 行第 \(j\) 个整数表示涂色完成后网格中第 \(i\) 行第 \(j\) 列的方格是什么颜色。
样例 #1
样例输入 #1
2
5 5 9
1 5 1
0 4 0
1 4 1
0 3 0
1 3 1
0 2 0
1 2 1
0 1 0
1 1 1
3 3 3
0 1 2
0 3 1
1 1 3
样例输出 #1
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
3 2 2
3 0 0
3 1 1
提示
【样例 1 解释】
注意当一个格子没有被涂色时,其颜色为白色,用数字 \(0\) 表示。
【样例 2】
见选手目录下的 paint/paint2.in 与 paint/paint2.ans。
【数据范围】
对于所有数据,保证:
- \(1 \leq T \leq 10\),\(1 \leq n,m \leq 10^5\),\(0 \leq q \leq 10^5\),\(0 \leq c_i \leq 10^9\)。
- 若 \(opt_i=0\),则 \(1 \leq x_i \leq n\);若 \(opt_i=1\),则 \(1 \leq x_i \leq m\)。
- 单个测试点中所有数据的 \(n \cdot m\) 的总和不超过 \(10^6\),\(q\) 的总和不超过 \(10^6\)。
| 测试点 | \(n \le\) | \(m \le\) | \(q \le\) | 性质 A | 性质 B |
|---|---|---|---|---|---|
| 1 | \(1\) | \(1\) | \(0\) | √ | √ |
| 2 | \(1\) | \(1\) | \(1\) | √ | √ |
| 3 | \(1\) | \(10\) | \(20\) | √ | √ |
| 4 | \(1\) | \(10^5\) | \(10^5\) | × | √ |
| 5 | \(1\) | \(10^5\) | \(10^5\) | × | √ |
| 6 | \(1\) | \(10^5\) | \(10^5\) | × | × |
| 7 | \(10\) | \(10\) | \(20\) | √ | √ |
| 8 | \(50\) | \(50\) | \(100\) | √ | √ |
| 9 | \(50\) | \(50\) | \(100\) | √ | × |
| 10 | \(1000\) | \(1000\) | \(2000\) | × | √ |
| 11 | \(1000\) | \(1000\) | \(2000\) | × | × |
| 12 | \(1000\) | \(1000\) | \(2000\) | × | × |
| 13 | \(1000\) | \(1000\) | \(10^5\) | × | × |
| 14 | \(1000\) | \(1000\) | \(10^5\) | × | × |
| 15 | \(10^5\) | \(10^5\) | \(10^5\) | √ | √ |
| 16 | \(10^5\) | \(10^5\) | \(10^5\) | √ | √ |
| 17 | \(10^5\) | \(10^5\) | \(10^5\) | √ | × |
| 18 | \(10^5\) | \(10^5\) | \(10^5\) | √ | × |
| 19 | \(10^5\) | \(10^5\) | \(10^5\) | × | × |
| 20 | \(10^5\) | \(10^5\) | \(10^5\) | × | × |
特殊性质 A:保证测试点中所有的 \(q \cdot \max(n, m)\) 之和不超过 \(10^7\)。
特殊性质 B:保证 \(opt_i = 1\)。
【提示】
数据千万条,清空第一条。多测不清空,爆零两行泪。
题解
这个题其实非常简单,一个格子的颜色是由他的行和列决定的,先后涂色的话,让我想起了铺地毯那个题,所以我们用结构体记录每一行或者每一列的颜色,但是我们只记录颜色是不行的,我们得记录每一行或者每一列叠加的时间,最终每个格子的颜色时候叠加的时间决定的,这是这个题解题的第一部分,我们需要枚举t,枚举q,时间复杂度是\(O(tq)\)
下一步我们输出每个格子的颜色,但是我发现n和m非常大,但是\(n*m\)非常小,在时间复杂度方面,\(O(t*n*m)\)是可以接受的,但是要把这个二维矩阵存下来是不可能的,空间复杂度不允许,所以我们选择直接输出的方式。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005;
struct maxtr{
int ys,tt;
}h[maxn],l[maxn];
int t,n,m,q;
int main(){
scanf("%d",&t);
for(int k=1;k<=t;k++){
scanf("%d%d%d",&n,&m,&q);
memset(h,0,sizeof h);
memset(l,0,sizeof l);
for(int j=1;j<=q;j++){
int op,a,b;
scanf("%d%d%d",&op,&a,&b);
if(op==0){
h[a].ys=b;
h[a].tt=j;
}
if(op==1){
l[a].ys=b;
l[a].tt=j;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(h[i].tt>l[j].tt){
cout<<h[i].ys<<" ";
}else{
cout<<l[j].ys<<" ";
}
cout<<endl;
}
}
}
/**
1
3 3 3
0 1 2
0 3 1
1 1 3
*/