快速幂,快速乘,矩阵乘
快速幂
计算\(a^n(n\geqslant0)\),一般会对答案取个模
例如计算\(5^{11}\),考虑11二进制\((1011)_2\)有\(5^{11} = 5^8*5^2*5^1\)
将n的二进制中为1的位置对应的a的\(2^k\)次幂相乘就能得到最终结果
可以用\(O(\log{n})\)的时间复杂度计算a所有被用到的\(2^k\)
模板
int P = 1e9+7;
int quickpow(long long a, int n)
{
long long ans = 1;
for(; n; n >>= 1)
{
if(n & 1)
{
ans *= a;
ans %= P;
}
a *= a;
a %= P;
}
}
快速乘\(O(\log{b})\)
\(a*b\mod P\)
- \(0\leqslant{a,b}\leqslant{10^{9}},1\leqslant P \leqslant10^9\),开
long long直接算 - \(0\leqslant{a,b}\leqslant{10^{18}},1\leqslant P \leqslant10^9\),由于\((a*b)\%P=(a\%P*b\%P)\%P\)且取完模后并不会报
long long,乘之前分别取模 - \(0\leqslant{a,b}\leqslant{10^{18}},1\leqslant P \leqslant10^{18}\),怎么办?
考虑\(7*11\%P\),\((11)_{2}=1011\),有\(7*11 = 7*8 + 7*2 + 7*1\)
将b的二进制中为1的位置对应的\(2^k*a\)相加就能得到最终结果
模板:
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
LL quickmul(LL a, LL b, LL P)
{
LL ans = 0;
a %= P;
for(; b; b >>= 1)
{
if(b & 1) ans += a, ans %= P;
a += a;
a %= P;
}
return ans;
}
int main()
{
LL a,b,P; scanf("%lld%lld%lld",&a,&b,&P);
printf("%lld",quickmul(a,b,P));
return 0;
}
矩阵乘法
使用大写字母A,B表示矩阵,\(A_{i,j}\)表示矩阵A中第i行第j列的元素
\[\begin{array}{l} 假设A是一个n行m列矩阵,B为m行k列矩阵,C是一个行k列矩阵 \\ C = A * B \\ C_{i,j} = \sum^{m}_{k=1}A_{i,j}B_{i,j} \end{array} \]矩阵乘法满足结合律但不满足交换律
\[\begin{array}{l} (A * B) * C = A * (B * C) \\ A * B \neq B * A \end{array} \]暴力求复杂度\(O(nmk)\)
根据结合律性质,可以使用快速幂快速求出一个矩阵A的n次幂,因为在很多问题中,我们在处理递推公式或动态规划的转移方程时第i项的值可以由之前k项的值推得:
\[\begin{array}{l} f[i] = \sum^{k}_{j = 1} a_{j}*f[i-j] \\ 构造矩阵 \\ A = \left( \begin{array}{cc} 0 & 0 & \dots & 0 & a_{k} \\ 1 & 0 & \dots & 0 & a_{k-1} \\ 0 & 1 & \dots & 0 & a_{k-2} \\ \dots \\ 0 & 0 & \dots & 1 & a_1 \end{array} \right) \\ (f[i-k] \dots f[i-2] f[i-1]) * A = (f[i-k+1] \dots f[i-1] f[i]) \\ (f[1] \dots f[k-1] f[k]) * A^{n-k} = (f[n-k+1] \dots f[n-1] f[n]) \end{array} \]时间复杂度\(O(k^{3}\log{n})\)
模板:
int n;
LL a[N+1][N+1],f[N+1];
void aa()
{
LL w[N+1][N+1];
memset(w,0,sizeof(w));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++)
w[i][j] = a[i][k] * a[k][j],
w[i][j] %= P;
memcpy(a,w,sizeof(a));
}
void fa()
{
LL w[N+1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f,w,sizeof(f));
}
void matrixpow(int k)
{
for(; k; k >>= 1)
{
if(k & 1) fa();
aa();
}
}
可以进一步将一定为0的位置省略计算优化
const int N = 200, P = 1e9+10;
int n;
LL a[N+1][N+1],f[N+1];
void aa()
{
LL w[N+1][N+1];
memset(w,0,sizeof(w));
for(int i = 1; i <= n; i++)
for(int k = 1; k <= n; k++)
if(a[i][k])
for(int j = 1; j <= n; j++)
if(a[k][j])
w[i][j] += a[i][k] * a[k][j],
w[i][j] %= P;
memcpy(a,w,sizeof(a));
}
void fa()
{
LL w[N+1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f,w,sizeof(f));
}
void matrixpow(int k)
{
for(; k; k >>= 1)
{
if(k & 1) fa();
aa();
}
}
例题
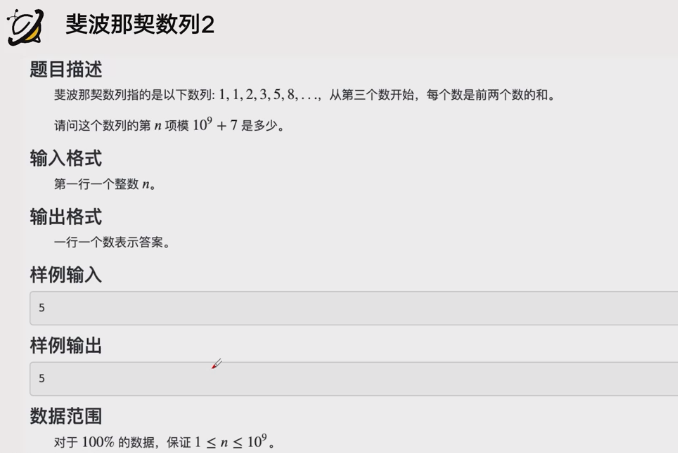
推出来的公式
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 2, P = 1e9+7;
int n = 2;
int k;
LL f[N+1],a[N+1][N+1];
void aa()
{
LL w[N+1][N+1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= n; i++)
for(int k = 1; k <= n; k++)
if(a[i][k])
for(int j = 1; j <= n; j++)
if(a[k][j])
w[i][j] += a[i][k] * a[k][j],
w[i][j] %= P;
memcpy(a, w, sizeof(a));
}
void fa()
{
LL w[N+1];
memset(w,0,sizeof(w));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f, w, sizeof(f));
}
void output()
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
cout<<a[i][j]<<" ";
}
cout<<endl;
}
}
void matrixpow(LL k)
{
for(; k; k>>=1)
{
if(k & 1) fa();
aa();
// output();
}
}
int main()
{
scanf("%d",&k);
f[1] = 0, f[2] = 1;
a[1][1] = 0, a[1][2] = 1;
a[2][1] = 1, a[2][2] = 1;
matrixpow(k-1);
printf("%lld",f[2]);
return 0;
}
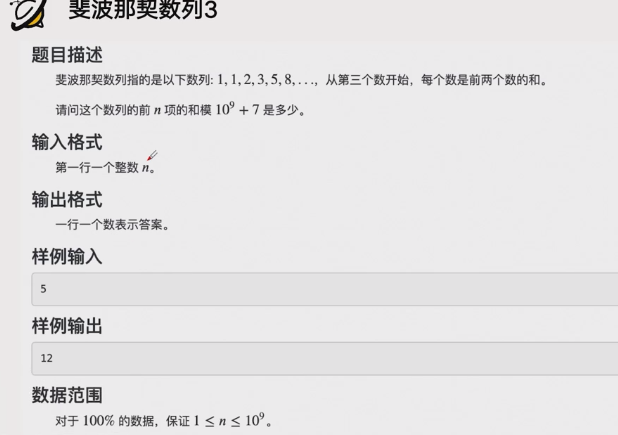
套路: 求前多少项的和就在矩阵中多加一行一列即可
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 3, P = 1e9+7;
int k;
LL f[N+1],a[N+1][N+1];
void aa()
{
LL w[N + 1][N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= N; i++)
for(int k = 1; k <= N; k++)
if(a[i][k])
for(int j = 1; j <= N; j++)
if(a[k][j])
w[i][j] += a[i][k] * a[k][j];
memcpy(a, w, sizeof(a));
}
void fa()
{
LL w[N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f, w, sizeof(f));
}
void martixpow(LL k)
{
for(; k; k >>= 1)
{
if(k & 1) fa();
aa();
}
}
int main()
{
cin>>k;
f[1] = 0, f[2] = 1, f[3] = 0;
a[1][1] = 0, a[1][2] = 1, a[1][3] = 0;
a[2][1] = 1, a[2][2] = 1, a[2][3] = 1;
a[3][1] = 0, a[3][2] = 0, a[3][3] = 1;
martixpow(k);
printf("%lld",f[3]);
return 0;
}
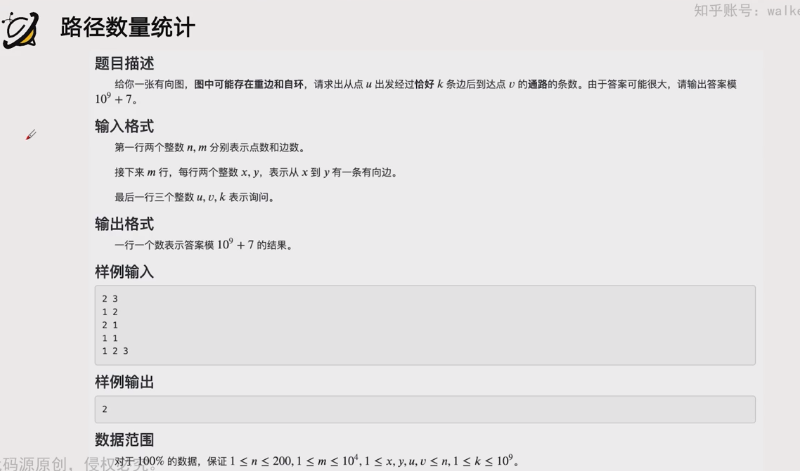
使用dp的话k的复杂度太高,使用矩阵的话可以将k的复杂度省掉,此时f的定义则是经过i条边后可以到达的点
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 200, P = 1e9 + 10;
int n,m,u,v,k;
LL f[N + 1],a[N + 1][N + 1];
void aa()
{
LL w[N + 1][N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= N; i++)
for(int k = 1; k <= N; k++)
if(a[i][k])
for(int j = 1; j <= N; j++)
if(a[k][j])
w[i][j] += a[i][k] * a[k][j],
w[i][j] %= P;
memcpy(a, w, sizeof(a));
}
void fa()
{
LL w[N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= N ;i++)
for(int j = 1; j <= N; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f, w, sizeof(f));
}
void martixpow(int k)
{
for(; k; k >>= 1)
{
if(k & 1) fa();
aa();
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 0; i < m; i++)
{
int x, y; scanf("%d%d", &x, &y);
a[x][y]++;
}
scanf("%d%d%d", &u, &v, &k);
f[u] = 1;
martixpow(k);
printf("%lld", f[v]);
return 0;
}
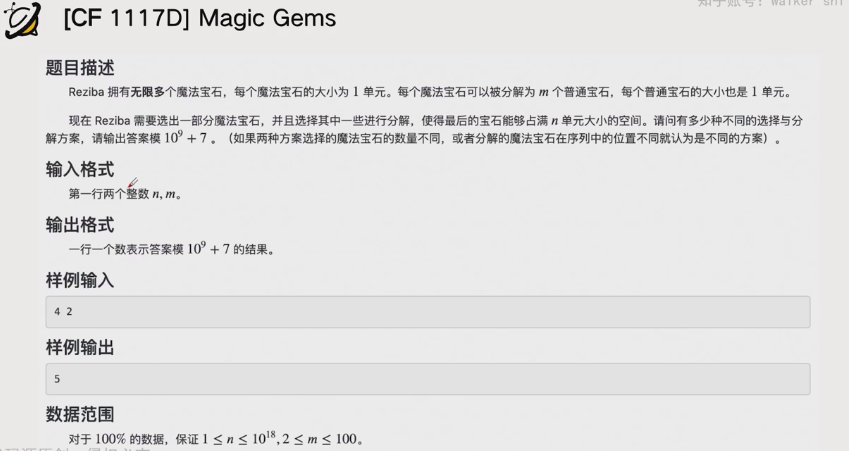
使用dp求状态\(f[n] = f[n-1] + f[n-m]\),但是效率不高,此时采用矩阵乘除最后一列外,其他如上述构造的矩阵,最后一个位置,n-1位和n-m位有贡献为1,此时只需要右上和右下为1即可
// Problem: D. Magic Gems
// Contest: Codeforces - Educational Codeforces Round 60 (Rated for Div. 2)
// URL: https://codeforces.com/problemset/problem/1117/D
// Memory Limit: 256 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 100, P = 1e9+7;
LL n, a[N + 1][N + 1], f[N + 1];
int m;
void aa()
{
LL w[N + 1][N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= m; i++)
for(int k = 1; k <= m; k++)
if(a[i][k])
for(int j = 1; j <= m; j++)
if(a[k][j])
w[i][j] += a[i][k] * a[k][j],
w[i][j] %= P;
memcpy(a, w, sizeof(a));
}
void fa()
{
LL w[N + 1];
memset(w, 0, sizeof(w));
for(int i = 1; i <= m; i++)
for(int j = 1; j <= m; j++)
w[i] += f[j] * a[j][i],
w[i] %= P;
memcpy(f, w, sizeof(f));
}
void martixpow(LL k)
{
for(; k; k >>= 1)
{
if(k & 1) fa();
aa();
}
}
int main()
{
scanf("%lld%d",&n,&m);
for(int i = 2; i <= m; i++) a[i][i-1] = 1;
a[1][m] = 1;
a[m][m] = 1;
f[m] = 1;
martixpow(n);
printf("%lld\n", f[m]);
return 0;
}