标签：le int ll 选讲 多校 sdfz sum dp mod

杂题选讲

20231212

《批题乱讲》

[ARC132E] Paw - 期望 + 计数

AT_arc132_e [ARC132E] Paw

长为 \(n\) 的字符串，每个地方可能是 <>. 每次随机一个 . 的地方，然后等概率向左向右。直到走出边界或者走到 . 。

路上会留下相同方向的符号。 问最后期望 < 的个数有多少。

\(1 \le n \le 10^5\)。

首先可以拿一种最终情况去分析，

发现最终的情况一定是 <<<<<=>>>>> 其中 = 表示不变（即原来的字符串）。

于是我们就可以去枚举每一个 = 的地方，一共有 \(n\) 个，

每次只要我们知道左右情况的概率即可。

那么我们设 \(f_i\) 表示 \(i\) 个洞之前全部变成 < 的概率，

由于对于第 \(i\) 个洞，除去最右边的往右走的情况，其他一定都是满足条件的，因为都是会被后面的洞走过来覆盖掉，

于是 \(f_i = f_{i-1} \times (1 - \frac{1}{2i})\)。

最终答案就很好算了，直接用 \(f_{左边点数} \times f_{右边点数} \times (cnt_{中间个数} + 左边点数)\) 算就可以了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=2e5+5;
const ll mod=998244353;
ll inv[N],f[N],ans=0;
int s[N],n,cnt=0,tp=0;
char str[N];

int main(){
  /*2023.12.13 H_W_Y [ARC132E] Paw 计数与期望*/
  scanf("%d%s",&n,str+1);inv[1]=f[0]=1ll;
  for(int i=1;i<=n;i++) if(str[i]=='.') s[++tp]=i;
  s[0]=0;s[tp+1]=n+1;
  for(int i=2;i<=(n<<1);i++) inv[i]=inv[mod%i]*(mod-mod/i)%mod;
  for(int i=1;i<=tp;i++) f[i]=f[i-1]*(mod+1-inv[2*i])%mod;
  for(int i=0;i<=tp;cnt=0,i++){
    for(int j=s[i]+1;j<s[i+1];j++) cnt+=(str[j]=='<');
    ans=(ans+1ll*(cnt+s[i])*f[i]%mod*f[tp-i]%mod)%mod;
  }
  printf("%lld\n",ans);
  return 0;
}

CF1610H Squid Game - 树形 dp - 好题！

CF1610H Squid Game

给定㇐个 \(n\) 个点的树，以及 \(m\) 条链。

你需要选取尽可能少的点， 使得对于每㇐条链 \((x_i , y_i)\)，都存在㇐个被选的 \(z\) 点，使得链上到 \(z\) 距离最短的点既不是 \(x_i\) 也不是 \(y_i\)。

\(n, m \le 3 \times 10^5\)。

好题啊。

首先可以知道树上的链分成了两种：直链 和 曲链，也就是说对于一条链 \((u,v)\)，如果其中一点是另一点的祖先，我们就把它叫做直链。

那么我们先来考虑一棵树是一条链的情况。

发现这个东西可以直接被转移到区间上面，那么每一条链就是这个样子：

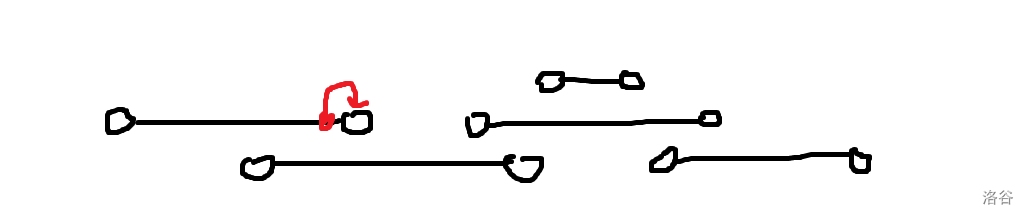
于是对于一个当前枚举到的点 \(i\)，也就是图中红色的点，它被选当且仅当下一个点是一条链的端点并且这条链没有被选过（这里我们称红色的点为这条链的关键点）。

我们现在把问题放到树上面，容易发现对于曲链，只要有一个点在它的 \(lca\) 上面就满足条件，那么我们最后再选一个根节点就一定满足条件，这样对答案的贡献只有 \(1\)，所以其实我们只需要考虑直链的情况。

和上面分析的方法类似，对于直链，我们也是尽可能让选的点深度更浅。

也就是说如果当前的节点 \(u\) 不是一条链的关键点（它上面的点不是一条链的上端点），那么 \(u\) 也是一定不会选的；而如果是，也不一定被选，因为有这样一种情况：

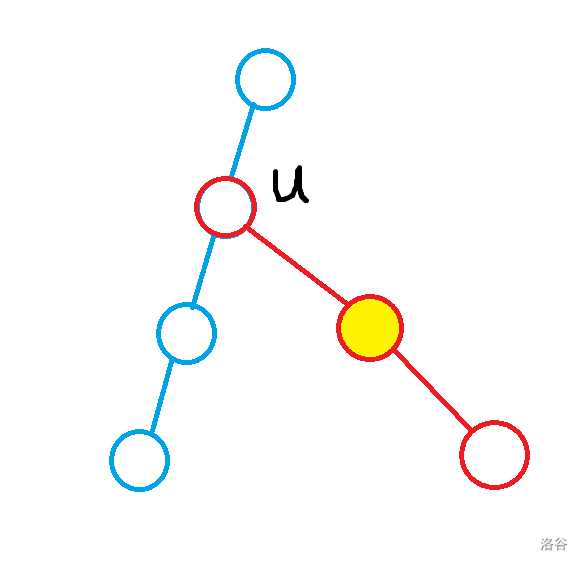
其中黄色是我们已经选的点，而蓝色和红色分别是链。

再这种情况中对于节点 \(u\) 而言，虽然它是蓝色链的关键点，但是我们也是不会选的，因为黄色点一定是可以满足条件的。

那么现在问题来了，到底什么时候才会去选 \(u\) 呢？

分析一下我们可以发现，有一条以 \(u\) 为关键点的链 \((x,y)\)（\(x\) 在 \(y\) 上面），它满足在 \(u\) 的子树中选的所有点都在 \(y\) 的子树中时，我们才会选 \(u\)。因为这个时候已选的所有点到链距离最小的点都是 \(y\)，反之在 \(y\) 子树外的一个选上的点是满足条件的。

于是现在我们考虑树形 dp，设 \(dp_u\) 表示只考虑关键点在 \(u\) 子树中的链，所需要选的点的最小值。

不考虑 \(u\) 这个点的贡献，很轻松可以得到 \(dp_u=\sum_{v \in son_u} dp_v\)。

而算上 \(u\) 的贡献就是：\(dp_u = \max(dp_u,dp_y+1)\)，其中 \(y\) 和前面的 \(y\) 意思一样。

这样为什么是对的？

很明显可以发现当 \(dp_u\) 变大的时候当且仅当 \(dp_y\) 与此时的 \(dp_u\) 相等，也就是说所有选的点都在 \(y\) 的子树中，这和我们上面分析的一致。

于是现在直链都解决了，剩下的就是曲链了。

发现这也是很好做的，如果有曲链不满足条件我们就直接选上 \(1\) 号节点即可。

而判断是否要选的思路和上面是类似的，对于一条曲链 \((x,y)\)，它需要再选上 \(1\) 当前仅当所有选的点都在 \(x\) 和 \(y\) 的子树中，也就是 \(dp_x+dp_y =dp_1\)。

于是统计答案的时候我们先令 \(ans=dp_1\)，那么就变成了 \(ans=\max(ans,dp_x+dp_y+1)\)。

这道题就做完了，代码也是好写的。

#include <bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back

const int N=5e5+5;
int n,m,head[N],tot=0,dp[N],ans=0,f[N][22],dep[N];
vector<int> g[N];
vector<pii> p;
struct edge{int v,nxt;}e[N<<1];

void add(int u,int v){
  e[++tot]=(edge){v,head[u]};head[u]=tot;
  e[++tot]=(edge){u,head[v]};head[v]=tot;
}

void init(int u,int fa){
  f[u][0]=fa;dep[u]=dep[fa]+1;
  for(int i=1;f[f[u][i-1]][i-1];i++) f[u][i]=f[f[u][i-1]][i-1];
  for(int i=head[u];i;i=e[i].nxt){
  	int v=e[i].v;
  	if(v==fa) continue;
  	init(v,u);
  }
}

int lca(int u,int v){
  if(dep[u]<dep[v]) swap(u,v);
  for(int i=19;i>=0;i--)
  	if(dep[f[u][i]]>dep[v]) u=f[u][i];
  return (f[u][0]==v)?u:-1; 
}

void dfs(int u,int fa){
  dp[u]=0;
  for(int i=head[u];i;i=e[i].nxt){
  	int v=e[i].v;
  	if(v==fa) continue;
  	dfs(v,u);dp[u]+=dp[v];
  }
  for(auto i:g[u]) dp[u]=max(dp[u],dp[i]+1);
}

int main(){
  /*2023.12.13 H_W_Y CF1610H Squid Game 树形dp*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m;
  for(int i=2,x;i<=n;i++) cin>>x,add(i,x);
  init(1,0);
  for(int i=1,u,v;i<=m;i++){
  	cin>>u>>v;
  	int nw=lca(u,v);
  	if(nw==-1) p.pb({u,v});
  	else{
  	  if(abs(dep[u]-dep[v])==1) cout<<"-1",exit(0);
  	  g[nw].pb(dep[u]>dep[v]?u:v);
  	}
  }
  dfs(1,0);ans=dp[1];
  for(auto i:p) ans=max(ans,dp[i.fi]+dp[i.se]+1);
  cout<<ans<<'\n';
  return 0;
}

写了一篇题解

CF704C Black Widow - 建图 + dp

CF704C Black Widow

给定 \(m\) 个布尔变量 \(x_1, x_2, \ldots, x_m\)，以及 \(n\) 个形如 \(x_i\) 或者 \(x_i \ \mathrm{or} \ x_j\) 的布尔表达式，其中规定 \(x_{-i}=\lnot x_i\)。并且，保证 \(x_i\) 和 \(x_{-i}\) 在所有的布尔表达式中一共只会出现最多两次。

请你求出，在一共 \(2^m\) 种布尔变量取值的情况下，有多少种情况，使得所有布尔表达式的值的异或为 \(1\)。此处认为，\(\rm True\) 为 \(1\)，\(\rm False\) 为 \(0\)。

由于结果可能过大，请输出答案模 \(10^9+7\) 的结果。

\(1 \leq n,m \leq 10^5\)。

首先容易发现这个东西总是想去建图。

因为一个 \(x_i\) 只会出现两次，所以我们建成的图一定是 链 或者 环。

我们以每一个表达式为节点，一条边表示一个变量，于是对于每一个连动块，是非常好算的。

我们直接设 \(g_{i,0/1,0/1}\) 表示前 \(i\) 个节点，前面的异或值为 \(0/1\)，它连出去的一条边的权值是 \(0/1\) 的方案数，

于是对于每一个连动块 dp 即可，而对于环的情况，我们直接暴力拆环，枚举那个节点选 \(0/1\) 分别 dp 即可。

但是这里存在了一些特殊的情况，比如只有一个点的连动块，

这是需要单独特判掉的，判断它是 \(x_i\) 还是 \(x_i \or x_j\) 即可。

统计答案的时候也是很简单的，直接 dp 就行了。

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define ll long long

const int N=1e5+5;
const ll mod=1e9+7;
ll c[2],g[N][2][2],ans=0,f[N][2];
int n,m,d[N],cnt=0,vis[N];
vector<int> G[N],s,a[N],b[N];

void dfs(int u){
  vis[u]=cnt;s.pb(u);
  for(auto v:G[u]) if(!vis[v]) dfs(v);
} 

void dp(int l1,int r1,int l2,int r2){
  int t=s.size();
  for(int i=0;i<=t;i++)
    for(int j=0;j<2;j++)
      for(int k=0;k<2;k++)
        g[i][j][k]=0;
  if(!a[s[0]][1]||(abs(a[s[0]][1])!=abs(a[s[1]][0])&&abs(a[s[0]][1])!=abs(a[s[1]][1]))) swap(a[s[0]][0],a[s[0]][1]);
  for(int i=1;i<t;i++) if(abs(a[s[i]][0])!=abs(a[s[i-1]][1])) swap(a[s[i]][0],a[s[i]][1]);
  for(int i=l1;i<=r1;i++) g[0][0][i]=1ll;
  for(int i=1;i<=t;i++){
  	int x=a[s[i-1]][0],y=a[s[i-1]][1];
  	for(int j=0;j<2;j++)
  	  for(int p=0;p<2;p++)
  	    for(int q=0;q<2;q++)
  	      (g[i][(((x<0)^p)|((y<0)^q))^j][q]+=g[i-1][j][p])%=mod;
  }
  for(int i=0;i<2;i++)
    for(int j=l2;j<=r2;j++)
      (c[i]+=g[t][i][j])%=mod;
}

void sol(){
  if(s.size()==1){
  	int x=s[0];
  	if(a[x].size()==1) return c[0]=c[1]=1,void();
  	if(abs(a[x][0])!=abs(a[x][1])) return c[0]=1,c[1]=3,void();
  	if(a[x][0]==a[x][1]) return c[0]=c[1]=1,void();
  	return c[0]=0,c[1]=2,void();
  }
  int rt=0;c[0]=c[1]=0;
  for(auto i:s) if(d[i]==1) rt=i;
  if(rt){
  	for(auto i:s) vis[i]=0;
  	s.clear();dfs(rt);
  	int x=s[0],l1=0,r1=1,l2=0,r2=1;
  	if(a[x].size()==1) a[x].pb(0),r1=0;
  	x=s.back();
  	if(a[x].size()==1) a[x].pb(0),r2=0;
  	return dp(l1,r1,l2,r2);
  }
  dp(0,0,0,0),dp(1,1,1,1);
}

int main(){
  /*2023.12.14 H_W_Y CF704C Black Widow dp*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m;ans=f[0][0]=1ll;
  for(int i=1,op,x;i<=n;i++){
  	cin>>op;
  	while(op--) cin>>x,a[i].pb(x),b[abs(x)].pb(i);
  }
  for(int i=1;i<=m;i++){
  	if(b[i].size()==2){
  	  int x=b[i][0],y=b[i][1];
  	  G[x].pb(y);G[y].pb(x);++d[x],++d[y];
  	}else if(b[i].size()==0) ans=ans*2ll%mod;
  }
  for(int i=1;i<=n;i++)
    if(!vis[i]){
      s.clear();++cnt;dfs(i);sol();
      for(int j=0;j<2;j++)
        f[cnt][j]=(1ll*f[cnt-1][j]*c[0]%mod+1ll*f[cnt-1][j^1]*c[1]%mod)%mod;
    }
  ans=ans*f[cnt][1]%mod;
  cout<<ans<<'\n';
  return 0;
}

CF839E Mother of Dragons - 最大团 + 记忆化

CF839E Mother of Dragons

给你一个 \(n\) 个节点的无向图 \(G=\{V,E\}\) 的邻接矩阵 。分配每个点的点权为 \(s_i\)，其中 \(\sum_{i=1}^n s_i = K\)，使得 \(\sum_{u,v \in E} s_u \times s_v\) 最大并求出其值。

\(1 \le n \le 40,1 \le k \le 1000\)。

首先需要得到一个结论：我们需要求的就是最大团。

为什么呢？（可以手玩一下）

如果 \(u,v\) 不在同一个块中，而 \(a_u =\sum_{e[u][i]=1} s_i,a_v= \sum_{e[v][i]=1}s_i\)，

那么对于 \(u,v\)，他们的贡献就是 \(a_u s_u + a_v s_v\)。

如果现在 \(a_u \ge a_v\)，那么把 \(s_v\) 变成 \(0\)，\(s_u=s_u+s_v\) 一定不会更劣，

所以我们最终保留下来的一定是最大团，

于是最大团中每一个元素的值平均一下就可以得到答案了。

而求最大团也是好求的，考虑记忆化搜索，

发现其实本质不同的状态只有 \(2^{\frac{2}{n}}\) 个，

对于每一个状态，我们就把它的 \(lowbit\) 找出来，枚举一下选不选它就可以了。

而由于你前面只有 \(2^{\frac{2}{n}}\) 次对于前面的点的枚举，

后面的 \(2^{\frac{2}{n}}\) 个状态被你记忆化掉了，所以只会枚举 \(2^{\frac{2}{n}}\) 次。

直接做就可以了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

int n,k;
ll e[45];
map<ll,int> f,mp;

int dfs(ll nw){
  if(nw==0) return 0;
  if(mp.count(nw)!=0) return mp[nw];
  ll lb=(nw&(-nw));
  return mp[nw]=max(dfs(nw-lb),dfs(nw&e[f[lb]])+1);
}

int main(){
  /*2023.12.14 H_W_Y CF839E Mother of Dragons 最大团 + 记忆化*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>k;
  for(int i=0;i<n;i++){
    f[1ll<<i]=i;
    for(int j=0,x;j<n;j++){
      cin>>x;
      if(x) e[i]|=(1ll<<j);
    }
  }
  double ans=dfs((1ll<<n)-1);
  ans=k*k/ans*(ans-1)/2;
  cout<<fixed<<setprecision(12)<<ans<<'\n';
  return 0;
}

CF1253F Cheap Robot - 图论 + Kruskal 重构树

CF1253F Cheap Robot

给你一张 \(N\) 个点的带权无向连通图，其中结点 \(1,2,…,k\) 为充电中心。

一个机器人在图中行走，假设机器人的电池容量为 \(c\)，则任何时刻，机器人的电量 \(x\) 都必须满足 \(0\le x\le c\)。如果机器人沿着一条边权为 \(w\) 的边从结点 \(i\) 走到结点 \(j\)，它的电量会减少 \(w\)。机器人可以在到达某个充电中心时把电量充满。

现在有 \(q\) 个询问，每次询问机器人要从 \(a\) 点到达 \(b\) 点，电池容量至少为多少，各个询问相互独立。保证 \(a\) 点和 \(b\) 点都是充电中心。

\(1 \le n,k \le 10^5,1 \le m,q \le 3 \times 10^5\)。

用树剖写 LCA 一直 TLE。。。

首先对于每一个节点，可以想到如果要充电一定时去最近的一个地方充电。

于是这是可以直接多元最短路求出来的，设点 \(i\) 到它最近的充电点距离是 \(dis_i\)。

这样假设现在我们有 \(x\) 的电量在 \(u\) 点，那么如果 \(x \lt dis_u\)，那它一定死了。

于是这时我们发现此时的 \(x\) 一定满足：

\[c-dis_u \ge x \ge dis_u \]

为什么呢？

毕竟它是从一个充电站来的，它的距离一定是 \(\ge dis_u\) 的，所以发现一个合法的电量 \(x\) 一定是满足这些条件的。

既然每次充电会让电量增加，那么我们每走一步就去充一次电回来一定不劣。

而我们希望从 \(u \to v\)，电量 \(x\) 是一定满足：

\[c-dis_u-w \ge dis_v\\ \therefore c \ge dis_u + dis_v +w \]

于是我们把每一条边的边权都变成 \(dis_u+dis_v+w\)，

直接跑一次 Kruskal 重构树即可，最后的答案就是路径上面的最大值。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fi first
#define se second
#define pb push_back

const int N=5e5+5;
const ll inf=1e18;
int n,m,k,s,cnt=0,head[N],tot=0,fa[N],Q,st[20][N],lg[N],idx=0,dfn[N];
struct edge{
  int u,v;ll w;
  bool operator <(const edge &rhs) const{
  	return w<rhs.w;
  }
}ed[N];
struct Edge{int v,nxt,w;}e[N<<1];
ll dis[N],val[N];
bool vis[N];

void dij(){
  priority_queue<pair<ll,int> > q;
  for(int i=0;i<=n;i++) dis[i]=inf;
  dis[s]=0,q.push({0,s});
  while(!q.empty()){
  	int u=q.top().second;q.pop();
  	if(vis[u]) continue;
  	vis[u]=true;
  	for(int i=head[u];i;i=e[i].nxt){
  	  int v=e[i].v;ll w=1ll*e[i].w;
  	  if(dis[v]>dis[u]+w){
  	  	dis[v]=dis[u]+w;
  	  	q.push({-dis[v],v});
  	  }
  	}
  }
}

void add(int u,int v,int w=0){
  e[++tot]=(Edge){v,head[u],w};head[u]=tot;
}

int find(int x){
  if(fa[x]==x) return x;
  return fa[x]=find(fa[x]);
}

void merge(int u,int v,ll w){
  u=find(u),v=find(v);
  if(u==v) return;
  ++cnt;add(cnt,u);add(cnt,v);
  val[cnt]=w,fa[u]=fa[v]=cnt;
}

void dfs(int u,int pre){
  dfn[u]=++idx;st[0][idx]=pre;
  for(int i=head[u];i;i=e[i].nxt) dfs(e[i].v,u);
}

int Min(int u,int v){return dfn[u]<dfn[v]?u:v;}

void init(){
  dfs(cnt,0);lg[1]=0;
  for(int i=2;i<=cnt;i++) lg[i]=lg[i/2]+1;
  for(int i=1;i<=lg[cnt]+1;i++)
    for(int j=1;j+(1<<i)-1<=cnt;j++)
      st[i][j]=Min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}

int lca(int u,int v){
  if(u==v) return u;
  u=dfn[u];v=dfn[v];
  if(u>v) swap(u,v);
  int s=lg[v-u];
  return Min(st[s][u+1],st[s][v-(1<<s)+1]);
}

int main(){
  /*2023.12.14 H_W_Y CF1253F Cheap Robot Kruskal + 图论*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m>>k>>Q;s=0;
  for(int i=1;i<=n*2;i++) fa[i]=i;
  for(int i=1,u,v,w;i<=m;i++) cin>>u>>v>>w,add(u,v,w),add(v,u,w),ed[i]=(edge){u,v,w};
  for(int i=1;i<=k;i++) add(s,i);
  dij();
  memset(head,0,sizeof(head));tot=0;
  for(int i=1;i<=m;i++) ed[i].w+=dis[ed[i].u]+dis[ed[i].v];
  sort(ed+1,ed+m+1);cnt=n;
  for(int i=1;i<=m;i++){
  	int u=ed[i].u,v=ed[i].v;ll w=ed[i].w;
    merge(u,v,w);
  }
  init();
  for(int i=1,u,v;i<=Q;i++) cin>>u>>v,cout<<val[lca(u,v)]<<'\n';
  return 0;
} 

CF1446D2 Frequency Problem (Hard Version) - 区间与众数 + lxlds

CF1446D2 Frequency Problem (Hard Version)

想不到吧，在 lxl 课件里面找到了。

给出\(n(1 \le n \le 200000)\)个元素组成的序列\(a_1,a_2,……,a_n\)。

求最长的子段使得其中有至少两个出现次数最多的元素。

输出最长子段长度。

首先我们需要得到一个结论，众数里面一定有一个是全局众数。

这还是比较显然的，因为我们发现如果这个区间中的众数不是全局众数，那么我们向外拓张一定可以再找到一个更大的区间使得有一个是全局众数。

于是我们直接枚举另一个众数是什么，求出最大的区间即可。

不管它合不合法，因为不合法会被更优的覆盖，这样时间复杂度是 \(\mathcal O(nV)\) 的。

优化就是考虑根号分治，但是我们没有那么写。

我们考虑其实每一次有很多不必要的数，

设当前枚举到的节点是 \(x\)，全局众数是 \(a\)。

对于每一个 \(x\) 出现的位置，我们将 \(a\) 出现位置集合中它的前驱后继找出来，标记，然后删掉。

于是这样我们就得到了 \(3 \times c(x)\) 个关键点，\(c(x)\) 为 \(x\) 的出现次数，而关键点就是我们标记过的点。

答案只会和这些点有关，容易证明，于是你再跑一边算答案即可。

如果用双指针可以做到 \(\mathcal O(n)\)，但是我写的还是 \(\log\) 的。

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define fi first
#define se second

const int N=5e5+5;
int n,ans=0,col=0,mx,c[N];
struct node{int v,c;}a[N];
vector<int> g[N],del;
vector<pair<int,int> > tg;
set<int> s;

bool bt(int x,int y){
  auto it=ub(g[mx].begin(),g[mx].end(),x);
  return it!=g[mx].end()&&*it<y;
}

int main(){
  /*2023.12.14 H_W_Y  CF1446D2 Frequency Problem (Hard Version) lxlds*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n;
  for(int i=1,x;i<=n;i++) cin>>x,g[x].pb(i),++c[x];
  mx=max_element(c+1,c+n+1)-c;
  for(auto i:g[mx]) s.insert(i);
  
  for(int x=1;x<=n;x++){
  	if(x==mx||!c[x]) continue;
  	for(auto j:del) s.insert(j);del.clear();
  	tg.clear();
  	for(auto j:g[x]){
  	  auto it=s.ub(j);
  	  if(it!=s.end()) tg.pb({*it,-1}),del.pb(*it),s.erase(it);
  	  tg.pb({j,1});
  	}
  	for(int j=g[x].size()-1;j>=0;j--){
  	  auto it=s.lb(g[x][j]);
  	  if(it!=s.begin()) tg.pb({*--it,-1}),del.pb(*it),s.erase(it);
  	}
  	sort(tg.begin(),tg.end());
  	tg.erase(unique(tg.begin(),tg.end()),tg.end());
  	for(auto i=tg.begin();i!=tg.end();++i){
  	  auto l=i;int lim,rim;
  	  for(;next(i)!=tg.end()&&!bt(i->fi,next(i)->fi);++i);
      auto it=lb(g[mx].begin(),g[mx].end(),l->fi),itr=ub(g[mx].begin(),g[mx].end(),i->fi);
      if(itr==g[mx].end()) rim=n;
      else rim=*itr-1;
      if(it==g[mx].begin()) lim=0;
      else lim=*--it;
      ++col;a[n]=(node){lim,col};
      int nw=0;
      for(auto j=l;j<=i;++j){
      	nw+=j->se;
      	if(a[nw+n].c==col) ans=max(ans,((j==i)?rim:(next(j)->fi-1))-a[nw+n].v);
      	else a[nw+n]=(node){j->fi,col};
      }
  	}
  }
  cout<<ans<<'\n';
  return 0;
}

CF1718D Permutation for Burenka - 笛卡尔树

CF1718D Permutation for Burenka

如果一个数组里面任意两个数字都是不同的，我们把这种数组称作为一个“纯数组”。举个例子。\([1,7,9]\) 是纯数组，\([1,3,3,7]\) 不是，因为 \(3\) 出现了两次。

如果两个纯数组 \(b,c\) 的长度相等且“类似”，并且对于所有数组中的 \(l\) 和 \(r (l \leq l \leq r \leq n)\)，都满足

\(\text{argmax}([b_l,b_{l+1}, \ldots, b_r])= \text{argmax}([c_l,c_{l+1}, \ldots, c_r]).\)

\(\text{argmax(x)}\) 返回值是 \(x\) 中最大值的下标。举个例子，\(\text{argmax}([1337,179,57])=1.\)

最近，Tonya 发现 Burenka 非常喜欢长度为 \(n\) 的排列 \(p\)。 Tonya 为了让她开心，于是给她一个类似于 \(p\) 的数组。他已经修复了 \(a\) 的一些元素，但恰好缺少 \(k\) 个元素（在这些位置 \(a_i\) 暂时等于 \(0\)）。保证\(k≥2\)。此外，他有一个由 \(k-1\) 个数字组成的集合 \(S\)。

Tonya 意识到他缺少一个数字来填补 \(a\) 的空白，所以他决定买下它。他有 \(q\) 个购买的选项。 Tonya 认为数字 \(d\) 适合他，如果可以用来自 \(S\) 的数字和数字 \(d\) 替换 \(a\) 中的所有零，那么 \(a\) 就变成了一个类似于 \(p\) 的纯数组。对于 \(d\) 的每个选项，输出这个数字是否适合他。

\(1 \le n,q \le 3\times 10^5\)。

挺有意思的一道题。

一开始以为是最大最小都相同，结果写完大意了。

首先容易发现两个序列本质相同其实就是他们所建立出来的笛卡尔树相同，

于是对于排列 \(p\)，我们可以先把它的笛卡尔树建出来，

这样每一个空的节点就有了一个区间 \([l,r]\)，一个方案合法当且仅当你可以把这 \(k\) 个数双射到这些区间中。

首先来想这个东西怎么判断，

我们如果把区间按照 \(r\) 排序，那么对于一个数满足的多个区间，我们一定是选走 \(r\) 最小的，

这样贪心的选择一定是不劣的。

而最终的 \(d\) 合法容易发现也是在一个区间中，那这个区间的上下界是什么？

我们可以用相同的贪心思路，

像上面那个从小到大的贪心，到了一个区间 \([l_i,r_i]\) 我们会发现没有合法的点了，

于是这个时候就需要 \(d\) 出场，它的下界就是 \(l_i\)，

如果贪心过程中两次出现需要 \(d\) 的情况，那么本来就不合法。

同理，找上界我们就按照 \(l\) 从大到小排序，同样从大到小枚举每一个点，

这样需要 \(d\)，的时候就可以得到上界，最后直接判断就可以了。

于是我们就做完了。

#include <bits/stdc++.h>
using namespace std;
#define pb push_back

const int N=3e5+5,inf=1e9;
int n,q,T,k,d[N],a[N],p[N],st[N],tp=0,lc[N],rc[N],b[N],l,r;
struct node{int l,r;};
vector<node> g;
set<int> s;
bool fl=false;

bool cmpl(const node &x,const node &y){return x.l>y.l;}
bool cmpr(const node &x,const node &y){return x.r<y.r;}

void dfs1(int u){
  if(!u) return;
  dfs1(lc[u]);dfs1(rc[u]);
  if(a[u]) d[u]=a[u]+1;
  else d[u]=max(1,max(d[lc[u]],d[rc[u]]));
}

void dfs2(int u,int lim){
  if(!u) return;
  if(!a[u]) g.pb((node){d[u],lim});
  else fl|=(a[u]>lim),lim=a[u]-1;
  dfs2(lc[u],lim);dfs2(rc[u],lim);
}

void sol(){
  cin>>n>>q;tp=l=k=0;r=inf;
  for(int i=1;i<=n;i++) cin>>p[i],lc[i]=rc[i]=d[i]=0;
  for(int i=1;i<=n;i++){
  	while(tp>0&&p[st[tp]]<p[i]) lc[i]=st[tp--];
  	rc[st[tp]]=i;st[++tp]=i;
  }
  
  lc[0]=rc[0]=fl=0;g.clear();
  for(int i=1;i<=n;i++) cin>>a[i],k+=!a[i];
  dfs1(st[1]);dfs2(st[1],inf);
  
  s.clear();
  for(int i=1;i<k;i++) cin>>b[i],s.insert(b[i]);
  sort(g.begin(),g.end(),cmpl);
  for(auto i:g){
  	auto it=s.upper_bound(i.r);
  	if(it==s.begin()||*--it<i.l){
  	  if(l){fl=1;break;}
  	  l=i.l;
  	}else s.erase(it);
  }
  
  s.clear();
  for(int i=1;i<k;i++) s.insert(b[i]);
  sort(g.begin(),g.end(),cmpr);
  for(auto i:g){
  	auto it=s.lower_bound(i.l);
  	if(it==s.end()||*it>i.r){
  	  if(r<inf){fl=1;break;}
  	  r=i.r;
  	}else s.erase(it);
  }
  
  while(q--){
  	int x;cin>>x;
  	if(!fl&&x>=l&&x<=r) cout<<"YES\n";
  	else cout<<"NO\n"; 
  }
}

int main(){
  /*2023.12.16 H_W_Y CF1718D Permutation for Burenka 笛卡尔树*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>T;
  while(T--) sol();
  return 0;
}

[ARC141C] Bracket and Permutation - 构造

AT_arc141_c [ARC141C] Bracket and Permutation

给你两个长度为 \(2\times n\) 的排列 \(P\) \(Q\)，还有一个要求的括号序列 \(S\)，长度也是 \(2\times n\)。定义一个长度为 \(2\times n\) 的排列 \(C\) 是合法的，当且仅当按照 \(S_{C_1} S_{C_2} \cdots S_{C_2\times n}\) 的顺序写下得到的字符串是合法的括号序列，其中 \(P\) 是合法的排列中字典序最小的，\(Q\) 是最大的，求 \(S\)。

\(1 \le n \le 2 \times 10^5\)。

差不多是自己想出来了，看来题解的写法——比我的好写多了。

首先我们可以通过这两个排列去推出一些东西，

比如对于排列 \(P={1,2,4,3}\)，那么很容易想到枚举到 \(i=3\) 时，我们发现这里应该时 \(3\)，为什么是 \(4\)？

而这是因为 \(3\) 不满足条件，于是稍微推一下就可以得到 \(3\) 是右括号，而 \(4\) 是左括号。

在分析 \(1,2,100\) 的情况，容易发现 \(3 \sim 99\) 全部是右括号，

但这些情况会在之后的位置一次被统计，所以我们其实只需要处理 \(3,100\) 即可。

于是我们对于每一个位置，我们都计算一个它应该是否什么值，

如果这个数不是应该的值，就进行上述的构造。

而正一次反一次一定可以构造玩所有位置，最后直接判断一下是否合法即可。

写代码的过程中我们用 \(c\) 数组维护为 \(0/1\) 是否被标记要好写得多。

#include <bits/stdc++.h>
using namespace std;

const int N=5e5+5;
int n,p[N],q[N],ans[N],cnt=0,m=0;
bool c[N][2],vis[N][2];
char s[N];
queue<int> Q;

int main(){
  /*2023.12.14 H_W_Y [ARC141C] Bracket and Permutation 构造*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n;
  for(int i=1;i<=(n<<1);i++) cin>>p[i];
  for(int i=1;i<=(n<<1);i++) cin>>q[i];
  int l=1,r=(n<<1);
  for(int i=1;i<=(n<<1);i++){
  	if(p[i]!=l){
  	  c[p[i]][0]=c[l][1]=true;
  	  vis[p[i]][0]=true;
  	}else{
  	  vis[l][0]=true;
  	  for(int j=l+1;j<=(n<<1);j++) if(!vis[j][0]){l=j;break;}
  	}
  	if(q[i]!=r){
  	  c[q[i]][0]=c[r][1]=true;
  	  vis[q[i]][1]=true;
  	}else{
  	  vis[r][1]=true;
  	  for(int j=r-1;j>=1;j--) if(!vis[j][1]){r=j;break;}
  	}
  }
  for(int i=1;i<=(n<<1);i++) if(!(c[i][0]^c[i][1])) cout<<"-1",exit(0);
  for(int i=1;i<=(n<<1);i++) s[i]=(c[i][0]?'(':')');
  cnt=m=0;
  while(!Q.empty()) Q.pop();
  for(int i=1;i<=(n<<1);i++){
  	if(s[i]=='('){
  	  ans[++m]=i;
  	  if(!Q.empty()) ans[++m]=Q.front(),Q.pop();
  	  else ++cnt;
  	}else{
  	  if(cnt) --cnt,ans[++m]=i;
  	  else Q.push(i);
  	}
  }
  for(int i=1;i<=(n<<1);i++) if(ans[i]!=p[i]) cout<<"-1",exit(0);
  cnt=m=0;
  while(!Q.empty()) Q.pop();
  for(int i=(n<<1);i>=1;i--){
  	if(s[i]=='('){
  	  ans[++m]=i;
  	  if(!Q.empty()) ans[++m]=Q.front(),Q.pop();
  	  else ++cnt; 
  	}else{
  	  if(cnt) --cnt,ans[++m]=i;
  	  else Q.push(i);
  	}
  }
  for(int i=1;i<=(n<<1);i++) if(ans[i]!=q[i]) cout<<"-1",exit(0);
  for(int i=1;i<=(n<<1);i++) cout<<s[i];
  return 0;
}

CF1603E A Perfect Problem - 构造 + 记忆化搜索

CF1603E A Perfect Problem

一个序列是好的当且仅当集合最大值乘上集合最小值大于等于集合元素的加和；

一个序列是完美的，当且仅当这个序列的任何子序列都是好的(包括自己不包括空集)；

你要求的是：长度为 \(n\) 的并且每一个元素都大于等于 \(1\) 并且小于等于 \(n+1\) 的完美序列的个数对 \(\mathrm{mod}\) 取模。

\(1 \le n \le 200\)。

这道题是一道需要发现很多性质的题目。。。

题解中有挺多什么 \(\mathcal O(n^6)\) 跑过的。

这里有 \(6\) 个性质：

1. 如果一个序列是好的，那么它排序之后的序列也是好的。
2. 如果所有子区间是好的，那么这个序列一定是完美的。（因为当一个区间是好的的时候，它的 \(\sum\) 是确定了的，于是一个区间是好的，它的子区间也是好的，那么就是完美的）
3. 如果一个序列所有前缀都是好的，那么序列就是好的。（通过上一个）
4. 对于所有的 \(i\)，有 \(a_i \ge i\)。（如果 \(a_i \lt i\)，那么前缀一定不是好的）
5. 如果 \(a_i = i\)，那么前面的所有都 \(=i\)。（易证）
6. 若 \(a_n = n+1,a_i \ge i+1\) 并且 \([1,n]\) 是好的，那么前缀就是好的。

根据这些性质，我们就可以进行 dp。

设 \(f_{i,s,k}\) 表示当前选了 \(i\) 个，前缀和是 \(s\)，将要选 \(k\)。

于是我们直接枚举一下选 \(k\) 的数量即可转移：

\[f_{i,s,k} = \frac{f_{i+cnt,s+k\times cnt,k+1}}{cnt!}s \]

于是直接记忆化搜索就行了。

而发现这个我们需要枚举 \(a_1\)，

但是考虑 \(a_1\) 一定很大，试了一下发现 \(a_1 \ge n-18\)，于是就做完了。

好抽象。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=205;
int n,fi;
ll mod,f[N][N][50],jc[N],inv[N],ans;
bool vis[N][N][50];

ll qpow(ll a,ll b){
  ll res=1ll;
  while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}
  return res;
}

void init(){
  jc[0]=1ll;
  for(int i=1;i<N;i++) jc[i]=1ll*jc[i-1]*i%mod;
  inv[N-1]=qpow(jc[N-1],mod-2);
  for(int i=N-1;i>=1;i--) inv[i-1]=1ll*inv[i]*i%mod;
}

ll dfs(int ct,int s,int cur,int lim){
  if(vis[ct][s][cur]) return f[ct][s][cur];
  vis[ct][s][cur]=true;
  ll &res=f[ct][s][cur];res=0;
  if(cur<=lim-1&&ct<cur) return res;
  if(cur==lim){
  	if(ct<n) res=inv[n-ct];
  	return res;
  }
  int x=n+1-cur-fi;
  for(int j=0;s+j*x<=fi&&ct+j<=n;j++)
    res=(res+dfs(ct+j,s+j*x,cur+1,lim)*inv[j]%mod)%mod;
  return res;
}

int main(){
  /*2023.12.16 H_W_Y CF1603F A Perfect Problem 构造 + 记忆化搜索*/ 
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>mod;init(); 
  for(int lim=0;lim<=18;lim++){
  	memset(vis,0,sizeof(vis));
  	fi=n+1-lim;
  	ans=(ans+dfs(0,0,0,lim))%mod;
  }
  ans=ans*jc[n]%mod;
  cout<<ans<<'\n';
  return 0;
}

CF1208H Red Blue Tree - lxlds + 二分 + 权值线段树 + 树剖 - 好题！

CF1208H Red Blue Tree

随机跳题让我做的，而且第一次就跳到它了。。。我认命了/kk

有一棵 \(n\) 个节点的树，然后给定一个数 \(k\)，

每个叶子结点都有一个固定的颜色（红或蓝），

其中红色用 \(0\) 表示，蓝色用 \(1\) 表示

对于每个非叶子节点 \(u\) 的儿子 \(v\)，如果 \(\sum (color_v=blue)-\sum (color_v=red)\ge k\)

那么这个节点就是蓝色的，否则就是红色的

现在要求支持三种操作：

1 v 输出 \(v\) 节点的颜色

2 v c 把 \(v\) 节点的颜色改为 \(c\)

3 h 把当前 \(k\) 的值改成 \(h\)

\(1 \le n \le 2 \times 10^5\)。

首先对于每一个节点的颜色是由它的所有儿子所决定的，也是极其不好维护的。

于是我们考虑换一种思路，发现对于每一个节点，他一定存在一个分界点 \(k_u\)，也就是 \(u\) 这个点的 \(k\) 值，

对于全局的 \(k\)，我们这个节点满足：

• 当 \(k \ge k_u\)，为红色，也就是 \(0\)。
• 当 \(k \lt k_u\)，为蓝色，也就是 \(1\)。

而容易发现 \(k_u\) 是单调的，

于是其实我们想找到最小的 \(k_u\) 使得当 \(k\) 值为 \(k_u\) 时，是红色，而 \(k=k_u-1\) 时，是蓝色。

直接在儿子中 二分 就可以得到答案了，

每次只需要判断是否满足 \(sz- 2 \sum_{v \in son_u} [k_v \le k_u] \lt k_u\)，也就是它的儿子中 \(cnt_1 -cnt_0\) 的个数比 \(k_u\) 小，那么这个节点一定是 \(0\)。

但是对于每一个节点判断是 \(\mathcal O(n \log n)\) 的，

如果我们建立一棵权值线段树，于是直接在线段树上面二分就可以把单次的时间复杂度做到 \(\mathcal O(\log n)\)。

做到这里，根据 lxlds 的基础，我们就很容易想到树剖了，

让每一个节点实际只维护它轻儿子的信息，得到一个轻儿子的 \(k\) 值，

于是再和重儿子的值合并一下就可以了，可是如何合并呢？

我们设重儿子的 \(k\) 值为 \(x\)，\(\Delta = k_u +2 \sum_{v \in lson_u} [k_v \le k_u]-sz \gt 0,cnt=\sum_{v \in lson_u} [k_v =k _u]\)。

于是我们可以分三种情况来讨论。

• \(x \gt k\)，于是 \(\Delta' = \Delta - 1\)，因为式子中的 \(sz ++\) 了。
  • \(\Delta \gt 1\)，那么变化对其是没有影响的，所以 \(k'=k\)。
  • \(\Delta = 1\)，那么变化会使 \(\Delta \gt 0\) 的条件不满足，于是 \(k'=k+1\)。
• \(x=k\)，那么 \(\Delta'=\Delta + 1\)，而 \(k\) 是不会变小，因为 \(-1\) 是一定不满足条件的（这样 \(x\) 就没有贡献了，而本来就不满足），所以 \(k'=k\)。
• \(x \lt k\)，同理 \(\Delta'=\Delta +1\)，此时 \(k\) 是可能减小的。
  • 假设 \(k'=k-1\)，那么 \(\Delta + 1 -2cnt -1\gt 0\) 满足条件，即 \(\Delta -2cnt \gt 0\)。
  • 反之不能减小，\(k'=k\)。

于是情况我们就推完了，于是对于每一个节点它的 \(k_u\)，我们可以把它变成一个三段函数，

而把这个三段函数在每一条重链上面维护好，查询的时候直接合并就可以了。

合并也是简单的，在重链上面的合并容易发现最后一定是一条链，于是直接用最后的 \(k\) 值即可（具体可以看代码）。

具体实现中，我们把每一条重链用二叉树维护，

这样才可以让每一次的查询做到 \(\mathcal O(\log n)\)，

而总的时间复杂度是 \(\mathcal O(n \log^2 n)\) 的。

#include <bits/stdc++.h>
using namespace std;
#define mid ((l+r)>>1)
#define pb push_back

const int N=2e5+5;
int n,K,q,col[N],head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];

struct SGT{//权值线段树维护每一个节点轻儿子的 k 值
   struct node{int v,s[2];}tr[N<<6];
   int idx=0;
   
   #define lc(p) tr[p].s[0]
   #define rc(p) tr[p].s[1]
   
  void pu(int p){
  	tr[p].v=tr[lc(p)].v+tr[rc(p)].v;
  }
  void upd(int l,int r,int &p,int x,int val){
    if(!p) p=++idx;
    if(l==r) return tr[p].v+=val,void();
    if(x<=mid) upd(l,mid,lc(p),x,val);
    else upd(mid+1,r,rc(p),x,val);pu(p);
  }
  int ct(int l,int r,int p,int x,int y){
  	if(!p) return 0;
  	if(x<=l&&y>=r) return tr[p].v;
  	if(y<=mid) return ct(l,mid,lc(p),x,y);
    if(x>mid) return ct(mid+1,r,rc(p),x,y);
    return ct(l,mid,lc(p),x,y)+ct(mid+1,r,rc(p),x,y);
  }
  int qry(int l,int r,int p,int pre,int m){
  	if(l==r) return l;
  	if(mid+2*(pre+tr[lc(p)].v)>m) return qry(l,mid,lc(p),pre,m);
  	return qry(mid+1,r,rc(p),pre+tr[lc(p)].v,m);
  }
}T;

void add(int u,int v){
  e[++tot]=(edge){v,head[u]};head[u]=tot;
  e[++tot]=(edge){u,head[v]};head[v]=tot;
}

int fa[N],top[N],son[N],sz[N],dep[N],lct[N],lrt[N];

void dfs1(int u,int pre){//树剖1
  dep[u]=dep[pre]+1;fa[u]=pre;son[u]=-1;sz[u]=1;
  for(int i=head[u];i;i=e[i].nxt){
  	int v=e[i].v;
  	if(v==pre) continue;
  	dfs1(v,u);sz[u]+=sz[v],++lct[u];
    if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
  }
  if(lct[u]) --lct[u];
}

void dfs2(int u,int pre){//树剖2
  top[u]=pre;
  if(son[u]==-1) return;
  dfs2(son[u],pre);
  for(int i=head[u];i;i=e[i].nxt) if(e[i].v!=son[u]&&e[i].v!=fa[u]) dfs2(e[i].v,e[i].v); 
}

int rt[N],pa[N],s[N][2];

bool isrt(int x){return s[pa[x]][0]!=x&&s[pa[x]][1]!=x;}

struct node{//维护每一个节点和区间的函数，有关 k
  int k,a,b,c;
  node(int x=0){k=a=b=c=x;}
  int operator ()(int x) const{return (x>k)?a:((x==k)?b:c);}
  friend node operator +(const node &f,const node &g){
  	node res=g;
  	res.a=f(g.a),res.b=f(g.b),res.c=f(g.c);
  	return res;
  }
}f[N],mul[N];

void pu(int p){
  mul[p]=f[p];
  if(s[p][1]) mul[p]=mul[p]+mul[s[p][1]];
  if(s[p][0]) mul[p]=mul[s[p][0]]+mul[p];
}

void upd(int x){//算出 x 的 f 函数
  int k=T.qry(-n-1,n+1,lrt[x],0,lct[x]);
  int delta=k+2*(T.ct(-n-1,n+1,lrt[x],-n-1,k))-lct[x],cnt=T.ct(-n-1,n+1,lrt[x],k,k);
  f[x].k=f[x].b=k;
  f[x].a=(delta==1)?k+1:k;
  f[x].c=(delta-2*cnt>0)?k-1:k;
}

int build(int l,int r,vector<int> &a){//二叉树维护一条重链
  if(l>r) return 0;
  int x=a[mid];
  s[x][0]=build(l,mid-1,a);
  if(s[x][0]) pa[s[x][0]]=x;
  s[x][1]=build(mid+1,r,a);
  if(s[x][1]) pa[s[x][1]]=x;
  pu(x);return x;
}

void dfs3(int u){//预处理每一条重链
  vector<int> nw;
  for(int x=u;x!=-1;x=son[x]) nw.pb(x);
  for(auto x:nw)
    for(int i=head[x];i;i=e[i].nxt){
      int v=e[i].v;
      if(v==son[x]||v==fa[x]) continue;
      dfs3(v),T.upd(-n-1,n+1,lrt[x],mul[rt[v]](0),1),pa[rt[v]]=x;
    }
  for(auto x:nw){
  	if(son[x]!=-1) upd(x);
  	else f[x]=(col[x]==0)?node(-n-1):node(n+1);
  }
  rt[u]=build(0,nw.size()-1,nw);
}

void mdf(int x){//修改 x 节点颜色
  f[x]=(col[x]==0)?node(-n-1):node(n+1);
  for(;x;x=pa[x]){
  	if(isrt(x)){
  	  T.upd(-n-1,n+1,lrt[pa[x]],mul[x](0),-1);
  	  pu(x);
  	  T.upd(-n-1,n+1,lrt[pa[x]],mul[x](0),1);
  	  upd(pa[x]);
  	}else pu(x);
  }
}

node qry(int x){//询问 x 节点的 k 值
  node res=f[x];
  if(s[x][1]) res=res+mul[s[x][1]];
  while(!isrt(x)){
  	if(x==s[pa[x]][0]){
  	  x=pa[x];res=res+f[x];
  	  if(s[x][1]) res=res+mul[s[x][1]];
  	}else x=pa[x];
  }
  return res;
}

int main(){
  /*2023.12.16 H_W_Y CF1208H Red Blue Tree 权值线段树 + 树剖*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>K;
  for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v);
  for(int i=1;i<=n;i++) cin>>col[i];
  dfs1(1,0);dfs2(1,1);dfs3(1);
  cin>>q;
  while(q--){
  	int op,v,c;
  	cin>>op;
  	if(op==1){
  	  cin>>v;node res=qry(v);
  	  cout<<(K<res(0))<<'\n';
  	}
  	else if(op==2){cin>>v>>c,col[v]=c,mdf(v);}
  	else cin>>K;
  }
  return 0;
}

[ARC154E] Reverse and Inversion - 逆序对与排列 + 期望

AT_arc154_e [ARC154E] Reverse and Inversion

给定 \(n,m\) 两个正整数和一个 \(n\) 的排列 \(P\)。重复进行如下操作 \(m\) 次：

• 选定 \(1\le i\le j\le n\)，并将 \(P_i,P_{i+1},..,P_j\) 翻转。

对于所有 \((\frac{n(n+1)}{2})^m\) 种方案，计算 \(\sum_{i<j}[P_i>P_j](j-i)\) 的值的和。

\(1 \le n,m \le 2 \times 10^5\)。

纯纯诈骗啊，我都要看出来了。

首先推式子，排列这个东西就是挺好的。

\[\begin{align} & \sum_{i\lt j}[P_i \gt P_j](j-i)\\ = & \sum_{i \lt j,P_i \gt P_j} j -\sum_{i \lt j,P_i \gt P_j} i\\ = & \sum_{i=1}^n i \cdot ( \sum_{j=1}^{i-1} [P_j \gt P_i] ) - \sum_{i=1}^n i\cdot (\sum_{j=i+1}^{n} [P_j \lt P_i])\\ = & \sum_{i=1}^n i ( \sum_{j=1}^{i-1} [P_j\gt P_i] - \sum_{j=i+1}^n [P_j \lt P_i] ) \end{align} \]

推到这里看似不太可以推了，但是发现是排列啊——全局比它小的也就 \(P_i -1\) 个，

于是这个的性质就多了，我们设前面比你大的有 \(x\) 个，这个式子有了后续。

\[\begin{align} & \sum_{i=1}^n i ( \sum_{j=1}^{i-1} [P_j\gt P_i] - \sum_{j=i+1}^n [P_j \lt P_i] )\\ = & \sum_{i=1}^n i (x-(n-i-(n-P_i-x)))\\ = & \sum_{i=1}^n i (i-P_i)\\ = & \sum_{i=1}^n i^2 - \sum_{i=1}^n iP_i \end{align} \]

这样一下就豁然开朗了。

于是我们现在就变成了求 \(i\) 最后到的位置的期望到达的位置，

首先有 \((1-\frac{2i(n-i+1)}{n(n+1)})^m\) 的概率，这些修改根本不影响到 \(i\)，于是 \(i\) 的期望就是它自己。

而对于碰到 \(i\) 的，我们发现把它移动到 \(j\) 和 \(n-j+1\) 的概率是一样的（可以画图理解），

于是 \(P_i\) 在这种情况下的期望位置就是 \(\frac{n+1}{2}\)，于是这道题直接做完了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long 

const int N=1e5+5;
const ll mod=998244353;
int n,m;
ll inv2,invn,ans=0;

ll qpow(ll a,ll b){
  ll res=1ll;a=(a+mod)%mod;
  while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}
  return res;
}

int main(){
  /*2023.12.16 H_W_Y [ARC154E] Reverse and Inversion 计数*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m;ans=0;
  inv2=qpow(2,mod-2);invn=qpow(1ll*n*(n+1)%mod,mod-2);
  for(int i=1,x;i<=n;i++){
  	cin>>x;
  	ll q=qpow((1-2ll*i*(n-i+1)%mod*invn%mod),m),s=q*i%mod+1ll*(1+mod-q)%mod*(n+1)%mod*inv2%mod;
    ans=(ans+1ll*i*i%mod-1ll*s*x%mod+mod)%mod;
  }
  ans=ans*qpow(1ll*n*(n+1)%mod*inv2%mod,m)%mod;
  cout<<ans<<'\n';
  return 0;
}

[ARC135D] Add to Square - 黑白染色 + 构造

AT_arc135_d [ARC135D] Add to Square

有一个 \(H \times W\) 的整数矩阵，你可以不断选择一个 \(2 \times 2\) 的区域都加上同一个整数，你需要最小化矩阵所有元素的绝对值的和，输出最小值并构造方案。

\(1 \le H,W \le 500\)。

又是一个矩阵，发现答案只会和绝对值有关，于是我们希望找到不变量。

将矩阵进行黑白染色（有点类似 CF1416F Showing Off 的做法了），

将黑色格子中的数取反，于是整个矩阵的答案是不变的，而每一次操作对一整行一整列的和就没有影响了。

于是我们现在希望构造一个最终的矩阵 \(B\)，使得它是答案并且可以和初始的矩阵 \(A\) 互相转化。

我们令 \(A\) 的每行每列的和为 \(x[i],y[j]\)，于是合法的 \(B\) 的每行每列和和 \(A\) 是相等的，因为每一次操作都是不会改变行列的和。

于是现在考虑如何构造 \(B\)，

发现我们就先当于要把 \(A\) 的 \(x[],y[]\) 都减成 \(0\)。

于是第一种是存在一个 \((i,j)\) 使得 \(x[i],y[j]\) 是同号的，那么我们直接把其中一个消成 \(0\)，一定没有多余的代价。

而如果不存在这样的二元组，我们就找两行或两列异号的，在第一行/第一列操作一下即可。

如果都不存在这两种情况，那一定是完成了，因为 \(\sum x[i]=\sum y[j]\) 的。

于是这样就做完了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long 

const int N=505;
int n,m;
ll b[N][N],x[N],y[N],a[N][N],ans=0;

void upd(int i,int j,ll s){b[i][j]+=s,x[i]-=s,y[j]-=s;}

int main(){
  /*2023.12.16 H_W_Y [ARC135D] Add to Square 黑白染色 + 构造*/
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m;
  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++){
      cin>>a[i][j];
      if((i+j)&1) a[i][j]=-a[i][j];
      x[i]+=a[i][j],y[j]+=a[i][j];
    }
  while(1){
  	int px1=0,px2=0,py1=0,py2=0;
    for(int i=1;i<=n;i++) (x[i]>0)?(px1=i):(x[i]<0?(px2=i):0);
    for(int j=1;j<=m;j++) (y[j]>0)?(py1=j):(y[j]<0?(py2=j):0);
    if(px1&&py1){upd(px1,py1,min(x[px1],y[py1]));continue;} 
    if(px2&&py2){upd(px2,py2,max(x[px2],y[py2]));continue;}
    if(px1&&px2){
      ll s=min(x[px1],-x[px2]);
      upd(px1,1,s);upd(px2,1,-s);
      continue;
    }
    if(py1&&py2){
      ll s=min(y[py1],-y[py2]);
      upd(1,py1,s);upd(1,py2,-s);
      continue;
    }
    break;
  }
  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++){
      if((i+j)&1) b[i][j]=-b[i][j];
      ans+=abs(b[i][j]);
    }
  cout<<ans<<'\n';
  for(int i=1;i<=n;i++,cout<<'\n')
    for(int j=1;j<=m;j++)
      cout<<b[i][j]<<' ';
  return 0;
}

[ARC149E] Sliding Window Sort - 计数 + 找循环节 - 好题！

AT_arc149_e [ARC149E] Sliding Window Sort

给定正整数 \(N,M,K\)。考虑对某个正整数数列 \(A=(A_0,\dots,A_{N-1})\) 做如下操作：

• 对所有 \(k=0,1,\dots,K-1\) 依次做一遍如下操作：
  • 将 \(A_{k\bmod N},A_{(k+1)\bmod N},\dots,A_{(k+M-1)\bmod N}\) 升序排序。

给定一个 \(1\sim N\) 间整数的排列 \(B=\{B_0,\dots,B_{N-1}\}\)。求经过上述操作后与 \(B\) 相同的 \(A\) 的数量，对 \(998244353\) 取模。

\(1 \le M \le N \le 3 \times 10^5,1 \le K \le 10^9\)。

深夜赶题，终于写完。

首先看着 \(K\) 那么大就不是什么好东西，这种情况只有两种：

1. 可以用倍增/矩阵快速幂优化。
2. 在经过一定次数的操作之后成环了。

而这道题的点就在于第二种。

我们发现他在经过 \(N-M+1\) 次操作后相当于把每一个数都进行了，

于是容易发现此时序列的最后 \(M-1\) 个就是全局的 \(M-1\) 大的数，并且还是排好序了的。

想象一下发现，后面的操作中也不会有大的变化了，也就是一个序列的循环，

就是这最大的 \(M-1\) 个数绕着序列转，每次把它后面的数交换到前面去，而这并不会影响什么。

所以对于 \(K \gt N-M+1\) 的情况我们是只用考虑 \(K=N-M+1\) 的情况；

而对于 \(K \lt N-M +1\) 的情况，发现后面的那些数根本没有用到，所以我们也是不用考虑的，于是也可以转化。

那么我们现在留下来就只需要考虑 \(K=N-M+1\) 的情况。

首先最大的 \(M-1\) 个数是可以乱排的，也就是有 \((M-1)!\) 种方案，

而我们剩下的那些数的位置，是有讲究的。

我们从给出的序列 \(B\) 入手，如果当前枚举到的 \(B_i\) 是前缀最大值，那么它在任意时刻进队都行，

因为前面比它小一定比它先出去，所以它是可以填在 \(A_0 \dots A_{i+M-1}\) 中任意没有被填过的位置，

于是对答案的贡献就是 \(M\)。

反之，那么一定有 \(A_{i+M-1} = B_i\)，因为它既然不是前缀最大值，那为什么前面有比它大的被淘汰了呢？

于是它就一定是新进来的那一个。

这样分析之后我们就做完了，主要是想清楚它的起始位置是什么。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=3e5+5;
const ll mod=998244353;
int n,m,k,b[N],a[N],cnt=0,mx=0;
ll ans=1ll;

int main(){
  /*2023.12.16 H_W_Y [ARC149E] Sliding Window Sort 计数问题*/ 
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>n>>m>>k;
  for(int i=0;i<n;i++) cin>>b[i];
  n=min(n,m+k-1);
  for(int i=0;i<n;i++) a[i]=b[i];
  sort(a,a+n);
  for(int i=0;i<n;i++) b[i]=lower_bound(a,a+n,b[i])-a+1;
  int pos=(m+k-2)%n;
  for(int i=1,j=pos;i<m;++i,j=(j-1+n)%n)
    if(b[j]!=n-i+1) cout<<"0\n",exit(0);
  k-=n-m+2;
  pos=((n-m+1-1ll*(m-1)*(k/(n-m+1)))%n+n)%n;
  for(int i=0,j=pos;i<n;i++,j=(j+1)%n)
    if(b[j]<=n-m+1) a[cnt++]=b[j];
  for(int i=1;i<m;i++) ans=1ll*ans*i%mod;
  for(int i=0;i<cnt;i++)
    if(a[i]>mx) mx=a[i],ans=1ll*ans*m%mod;
  cout<<ans<<'\n';
} 

Conclusion

1. 关于期望与计数问题，我们可以 随机找一个最终的情况 来分析性质。（[ARC132E] Paw）

2. 对于有关 bool 变量的题目我们都可以考虑建图用 dp 解决。（CF704C Black Widow）

3. 有关二进制的搜索我们常常考虑记忆化，每一次把状态的 \(lowbit\) 拿出来往下递归。（CF839E Mother of Dragons）

4. 在 lca 查询数达到 \(1e5\) 时，dfn 的 \(\mathcal O(1)\) 还是比树剖快太多了。（CF1253F Cheap Robot）

5. 有关枚举 值域 的问题我们可以考虑 根号分治。（CF1446D2 Frequency Problem (Hard Version)）

6. 线段树递归的函数名不要乱用——（交了 \(4\) 发得到数据，有看了好久。。。）（CF1208H Red Blue Tree）

   

   ct：其实我没用。

7. 当全局的“评判标准”要变时，我们考虑换成统计每一个节点改变值时的值。（CF1208H Red Blue Tree）

8. 有关 矩形或绝对值 的问题，我们可以考虑黑白染色，找到一些不变量从而解题。（[ARC135D] Add to Square）

9. 对于操作次数高达 \(10^9\) 的题目，我们一般考虑 倍增/矩阵快速幂 或者 找循环节。（[ARC149E] Sliding Window Sort）

10. 有关很多种情况的问题，我们考虑互相抵消（可以是期望，也可以是计数）。（[ARC154E] Reverse and Inversion）

11. 只要求区间子区间的最大值/最小值其中一个相同的问题可以转化成它们所构成的 笛卡尔树 的形态相同。（CF1718D Permutation for Burenka）

标签：le,int,ll,选讲,多校,sdfz,sum,dp,mod
From： https://www.cnblogs.com/hwy0622/p/20231212ztxj.html