珂朵莉树

珂朵莉树的适用范围是具有区间赋值操作且数据随机的题目。

珂朵莉树的思想在于随机数据下的区间赋值操作很可能让大量元素变为同一个数，所以我们以三元组<l,r,v>的形式保存数据（区间[l,r]中的元素的值都是v）：

struct node
{
    ll l, r;
    mutable ll v; // 这里mutable要写不然可能会CE
    node(ll l, ll r, ll v) : l(l), r(r), v(v) {} // 构造函数
    bool operator<(const node &o) const { return l < o.l; } // 重载小于运算符
};

用set存储三元组：

set<node> tree;

set会保证内部元素有序（便于插入、删除和查询），而mutable使得当整个结构体为const时，标为mutable的成员仍可变（便于区间加）。

• split()：区间操作可能会需要把原本连续的区间断开

auto split(ll pos)
// 若不支持C++14，auto须改为set<node>::iterator
{
    auto it = tree.lower_bound(node(pos, 0, 0)); // 寻找左端点大于等于pos的第一个节点
    // 若不支持C++11，auto须改为set<node>::iterator
    if (it != tree.end() && it->l == pos) // 如果已经存在以pos为左端点的节点，直接返回
        return it;
    it--; // 否则往前数一个节点
    ll l = it->l, r = it->r, v = it->v;
    tree.erase(it); // 删除该节点
    tree.insert(node(l, pos - 1, v)); // 插入<l,pos-1,v>和<pos,r,v>
    return tree.insert(node(pos, r, v)).first; // 返回以pos开头的那个节点的迭代器
                                               // insert默认返回值是一个pair，第一个成员是我们要的
}

原来：

执行split(4)后：(<2,4,2>变成<2,3,2>和<4,4,2>)

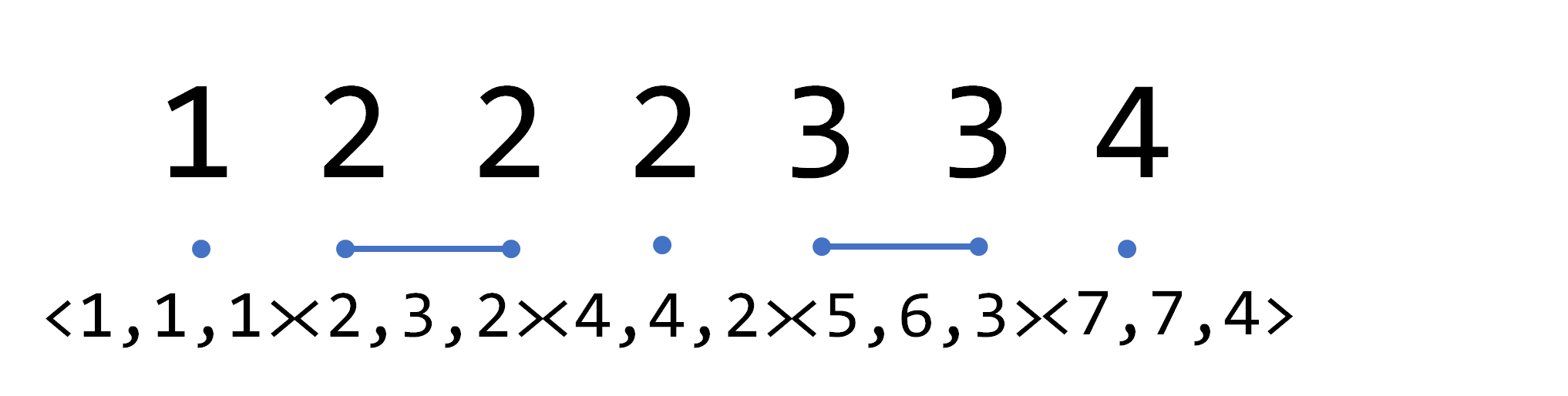
• assign()：区间赋值操作

void assign(ll l, ll r, ll v)
{
    auto end = split(r + 1), begin = split(l); // 顺序不能颠倒，否则可能RE
    tree.erase(begin, end); // 清除一系列节点
    tree.insert(node(l, r, v)); // 插入新的节点
}

即把范围内的节点全部删除，然后换上新的（范围更大的）节点。

注意求end和begin的顺序不能颠倒，因为split(end)可能把begin原来所在的节点断开。