模拟退火

引入

模拟退火，一种由金属退火启发的随机化（玄学）算法，。

当问题的方案数及其巨大甚至是无穷，而且不是一个线性或单峰函数时，模拟退火是一个较好的解决方案。

解释

先介绍一下它的前置算法——爬山算法。

爬山算法

爬山算法是一种局部择优的方法，采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。

说人话，也就是生成一个新解，将新解与当前最优解比较，如果更优，转移，否则不变，继续生成新解。

听不懂？举个可爱的例子。

假设我们现在有一个如下的单峰函数：

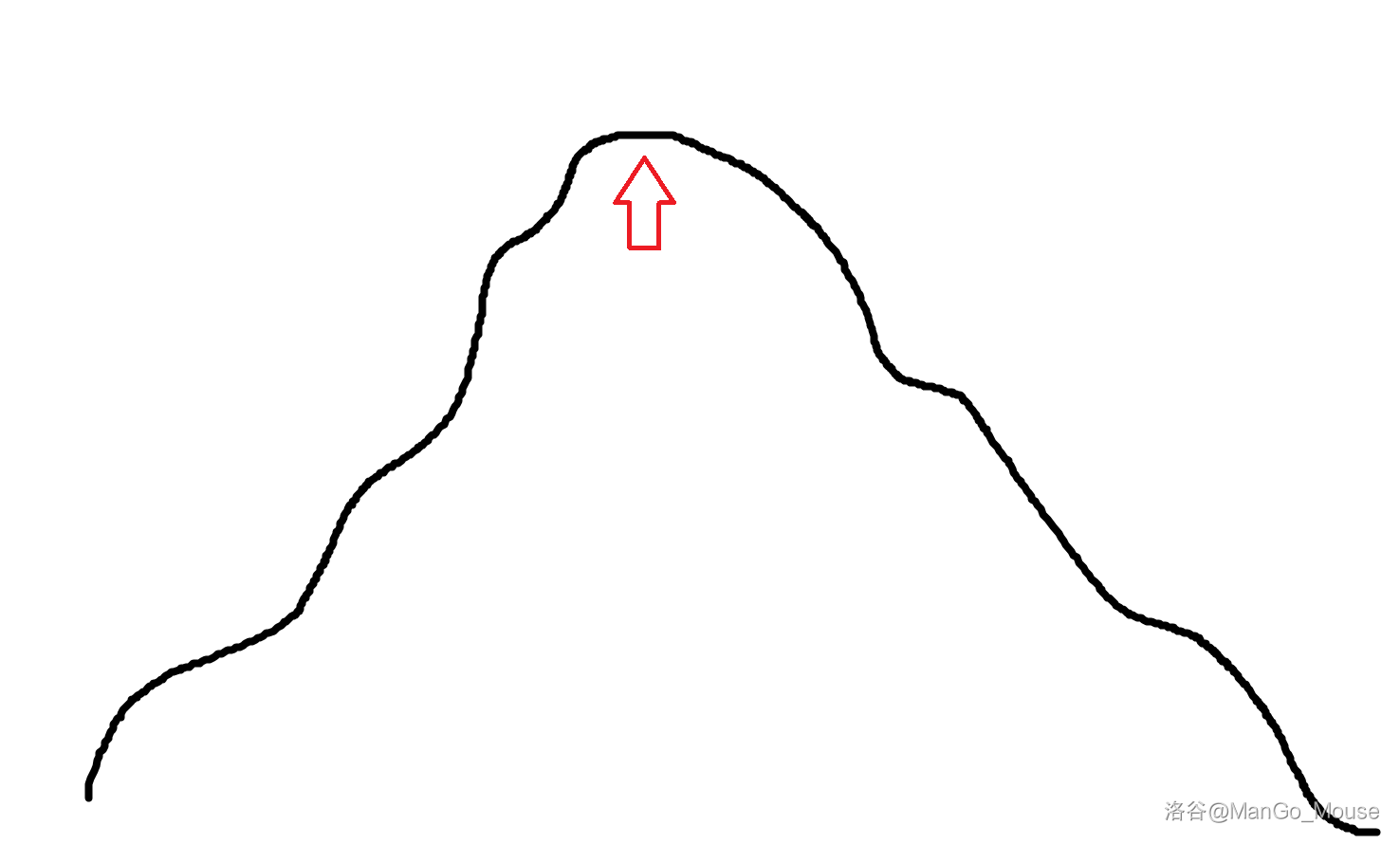
很明显，最优值就是红色箭头所在的地方。

把这个单峰函数比作一座山，可以举个例子：

现在有一只胡萝卜吃多了的软萌可爱的小兔纸，她的家在山顶（最优解）处，而她现在在山脚（初始值）。

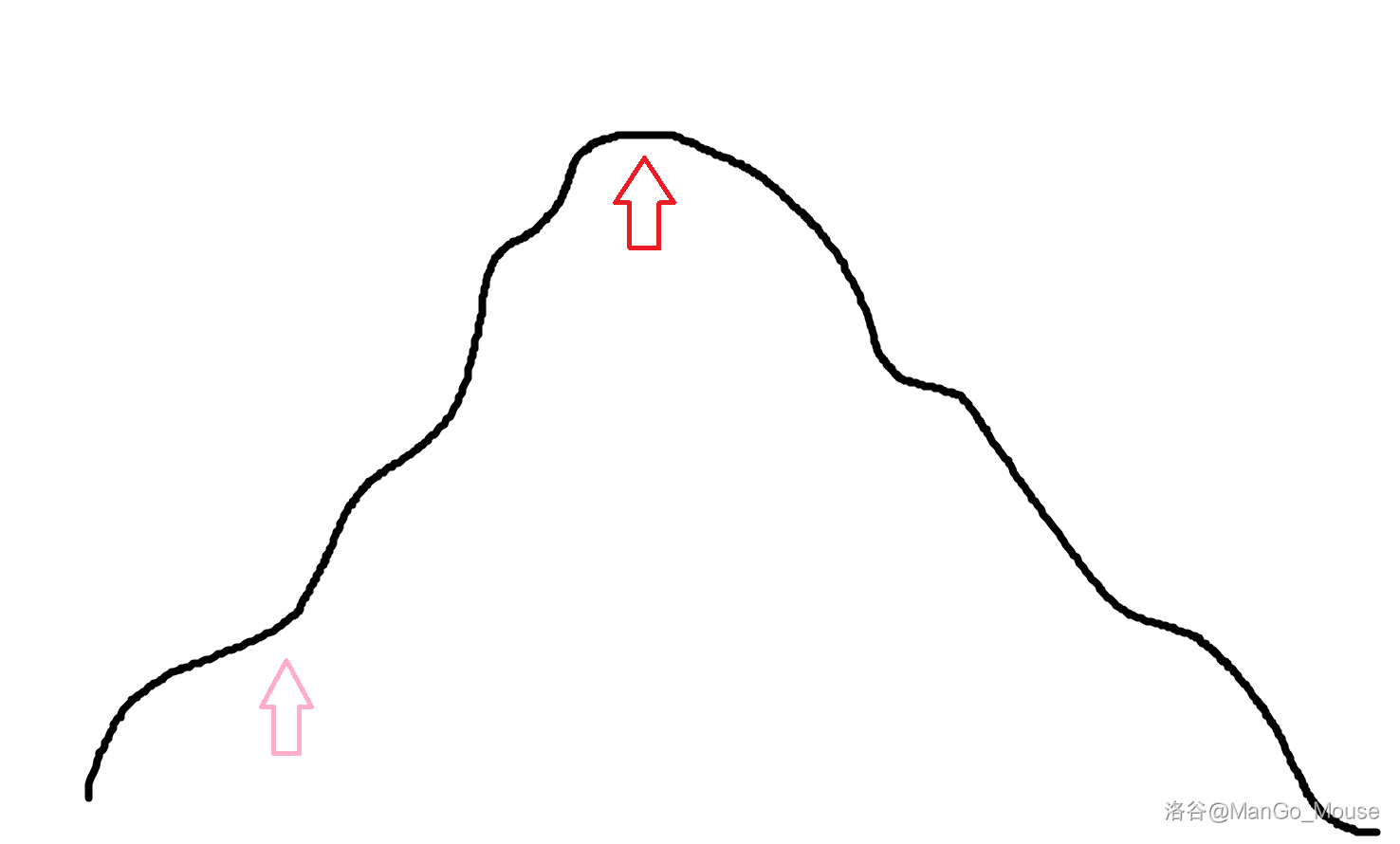
粉色箭头为小兔纸初始位置

她每次都跳一步，拿出气压计看看有没有比原先高（是否更优），如果是的，那么就从这里继续跳，否则，那就只好跳回去啦（回溯？）。

那就可以一步一步地走，一路 向云端（安安安安安安安~），一定会到家的。

但这样实在太慢了！万一这座山是珠穆朗玛峰，小兔纸变成冰雕了还没到家吧……

于是小兔纸想出一个办法，她一口气跳超级远，不就好啦。

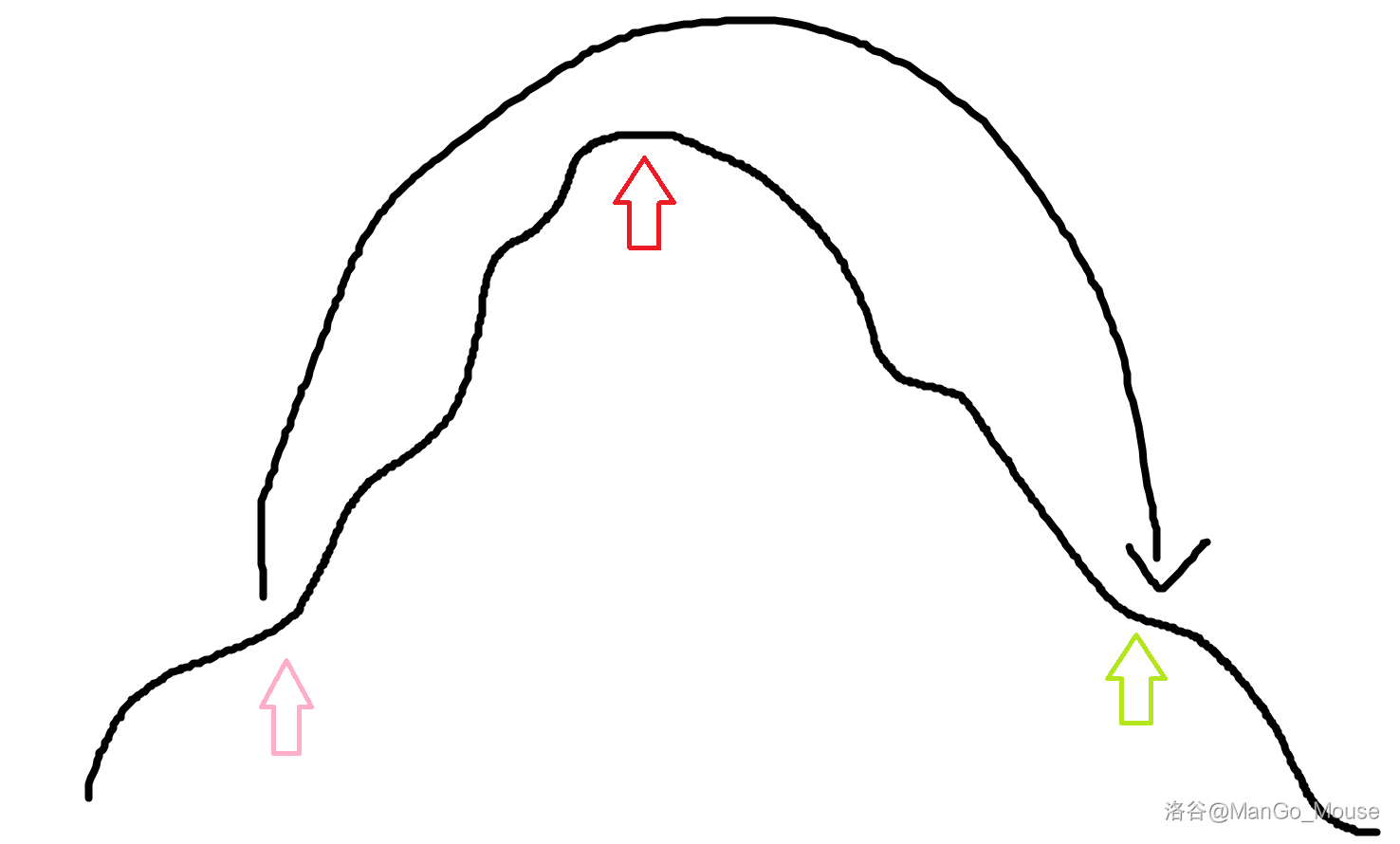
淡绿色为小兔纸跳跃后的位置

那确实挺快的，但又有个问题，跳的距离太远，不小心跳过山顶，就算她再翻过来，因为跳跃距离是固定的，还是会再次跳过山顶，那不就怎么跳都再也到不了家了吗？

所以就要改变策略，先一开始跳很远，然后慢慢地减少跳跃距离，越来越谨慎，这样就可以慢慢接近山顶了。

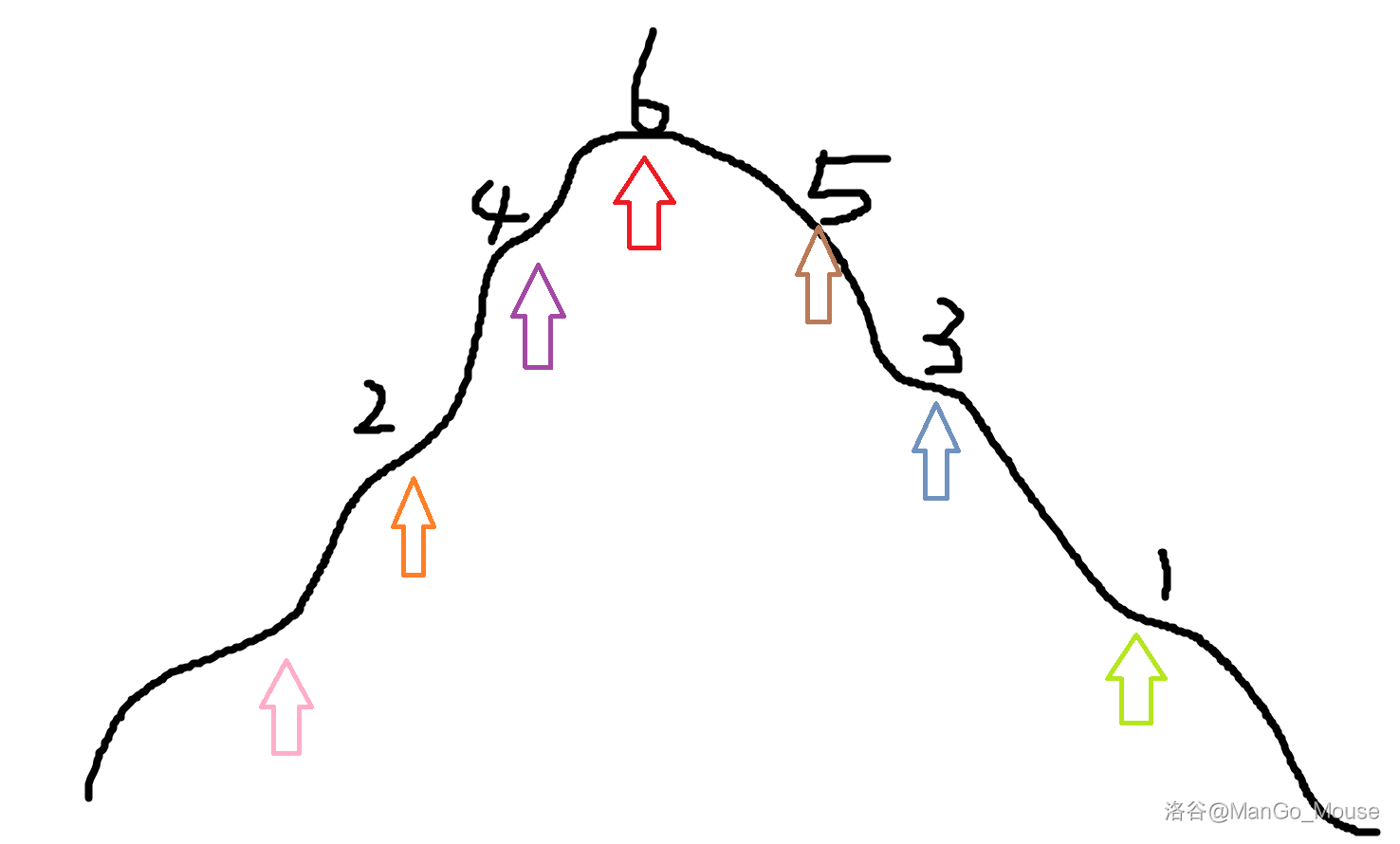
序号表示小兔子跳的顺序

就这样，小兔子终于到了家……

实现

一般来说，爬山需要利用一个名为⌈温度⌋的变量，温度可以理解为新解与当前最优解的更改幅度。

然后使用一个能量函数计算新解的能量，用于比较新解是否更优。

记得为当前最优解计算一个初始值。

例题：洛谷 P4035 [JSOI2008] 球形空间产生器

观察可以发现，这是一个单峰函数，爬山解决。

#include<bits/stdc++.h>
using namespace std;
const int N = 15;
const double d = 0.99995;
int n;
double dis[N],ans[N],cans[N],f[N][N];
double t = 10000;
void check(){ // 能量函数
	double res = 0;
	for(int i = 1;i <= n + 1;i ++){
		dis[i] = 0;
		cans[i] = 0;
		for(int j = 1;j <= n;j ++)
			dis[i] += (f[i][j] - ans[j]) * (f[i][j] - ans[j]);
		dis[i] = sqrt(dis[i]),res += dis[i];
	}
	res /= (n + 1);
	for(int i = 1;i <= n + 1;i ++)
		for(int j = 1;j <= n;j ++)
			cans[j] += (dis[i] - res) * (f[i][j] - ans[j]) / res;
}
int main(){
	cin>>n;
	for(int i = 1;i <= n + 1;i ++)
		for(int j = 1;j <= n;j ++)
			cin>>f[i][j],ans[j] += f[i][j];
	for(int i = 1;i <= n;i ++)
		ans[i] /= (n + 1);
	while(t >= 0.0001){
		check();
		for(int i = 1;i <= n;i ++)
			ans[i] += cans[i] * t; // 计算新解
		t *= d; // 降温
	}
	for(int i = 1;i <= n;i ++)
		printf("%.3lf ",ans[i]);
	return 0;
}

但是如果需要解决的问题不是单峰函数，而是一个多峰函数呢？

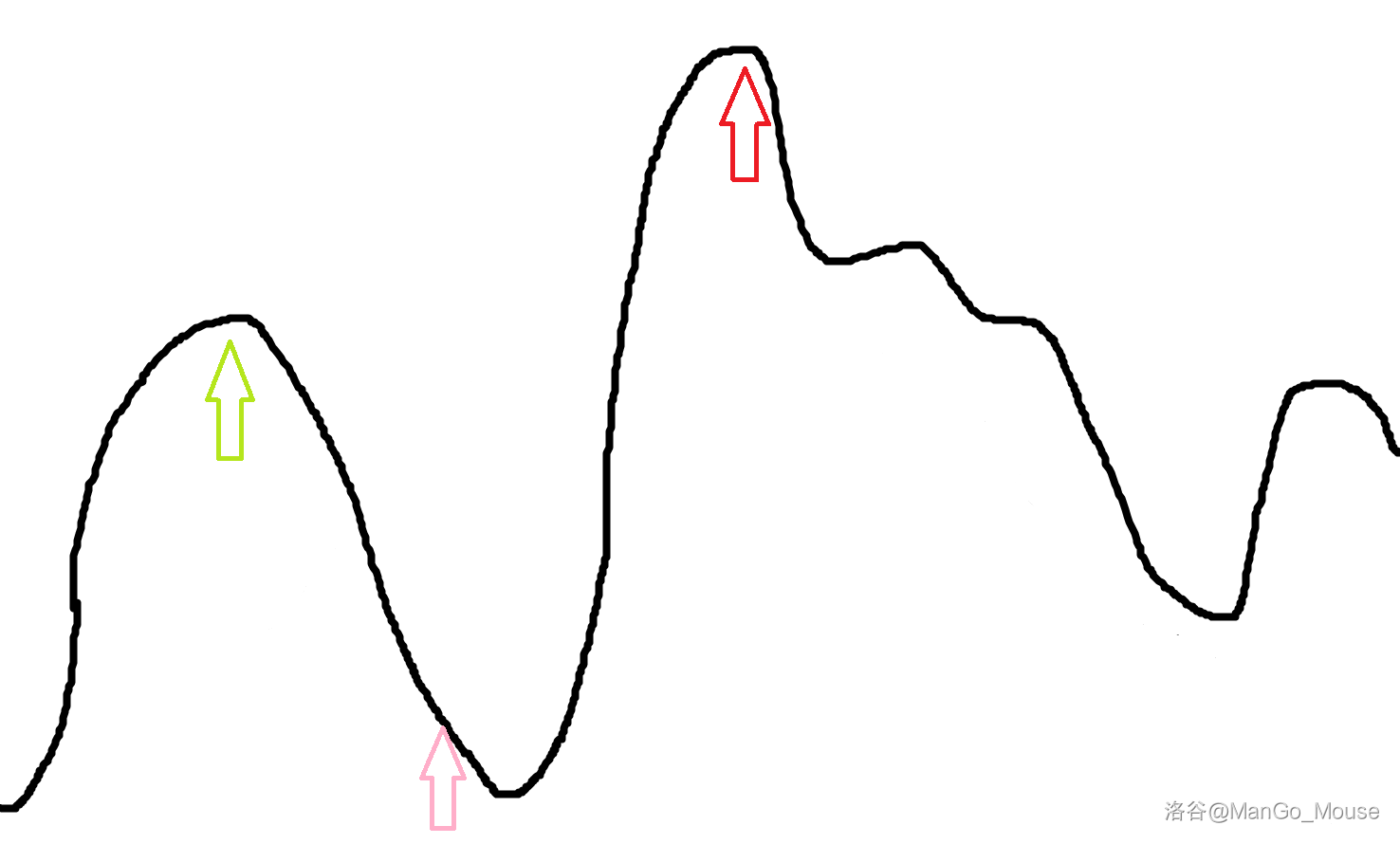
那么如果初始值为粉色箭头处，爬山算法就很有可能会找到绿色箭头处的局部最优解，但很明显，全局最优解应为红色箭头处。

这时候就该请出模拟退火了。