CF786B
题意:
定义 \((u,v,w)\) 表示 \(u\) 向 \(v\) 连了边权为 \(w\) 的边。
有三种连边操作
- \((u,v,w)\)
- \(\forall i\in [l,r],(u,i,w)\)
- \(\forall i\in [l,r],(i,u,w)\)
求最短路。
暴力加边是 \(O(nm)\) 的,考虑优化。
可以把图建到线段树上,线段树每个结点向左右儿子连 \(w=0\) 的边。那么对于 \(2\) 操作,只需要叶子结点 \(u\) 向对应区间连边即可,一次连边是 \(O(\log n)\) 的。
如下图:

假设现在 \(1\) 结点 向区间 \([2,4]\) 连 \(w=3\) 的边:

下面考虑 \(3\) 操作,只需要再建一棵线段树,每个结点向其父亲连 \(w=0\) 的边即可。
假设现在 \([1,3]\) 区间向 \(2\) 结点连 \(w=4\) 的边:
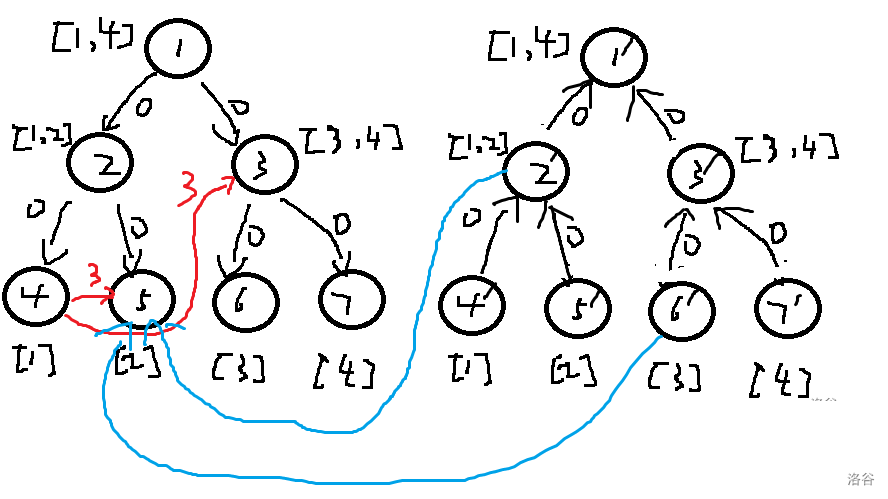
注意两棵树的叶子节点本质是同一个点,所以两点间也要连 \(w=0\) 的双向边。
那么这道题就解决了,总边数 \(O(8n+m\log n)\),跑最短路即可。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,K=4e5;
int n,m,s,id[N],vis[N*8];
long long d[N*8];
vector<pair<int,int>> G[N*8];
#define lc (k<<1)
#define rc (k<<1|1)
#define mid (l+r>>1)
void build(int k=1,int l=1,int r=n)
{
if(l==r) {id[l]=k;G[k].push_back({k+K,0}),G[k+K].push_back({k,0});return;}
G[k].push_back({lc,0}),G[k].push_back({rc,0});
G[lc+K].push_back({k+K,0}),G[rc+K].push_back({k+K,0});
build(lc,l,mid),build(rc,mid+1,r);
}
void upd(int x,int y,int u,int w,int op,int k=1,int l=1,int r=n)
{
if(l>=x&&r<=y)
{
if(!op) G[u].push_back({k,w});
else G[k+K].push_back({u,w});
return;
}
if(x<=mid) upd(x,y,u,w,op,lc,l,mid);
if(mid<y) upd(x,y,u,w,op,rc,mid+1,r);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>s;
build();
while(m--)
{
int op,u,v,l,r,w;cin>>op>>u;
if(op==1) {cin>>v>>w;G[id[u]].push_back({id[v],w});}
else {cin>>l>>r>>w;upd(l,r,id[u],w,op&1);}
}
memset(d,0x3f,sizeof(d));
priority_queue<pair<long long,int>> q;
q.push({0,id[s]});d[id[s]]=0;
while(!q.empty())
{
int u=q.top().second;q.pop();
if(vis[u]) continue;
vis[u]=1;
for(auto [v,w]:G[u]) if(d[u]+w<d[v]) d[v]=d[u]+w,q.push({-d[v],v});
}
for(int i=1;i<=n;i++) if(d[id[i]]>1e18) cout<<-1<<' ';else cout<<d[id[i]]<<' ';
}
P5025
优化建图 + 强连通分量。
注意 DAG 上不能 dp 点权和,改为对每个强连通分量求能引爆的区间。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e6+5,P=1e9+7;
int n,ans,tot,id[N],rev[N],vis[N],L[N],R[N],x[N],y[N],l[N],r[N];
vector<int> G[N],g[N];
#define lc (k<<1)
#define rc (k<<1|1)
#define mid (l+r>>1)
void build(int k=1,int l=1,int r=n)
{
tot=max(tot,k);
if(l==r) {id[l]=k,rev[k]=l;return;}
G[k].push_back(lc),G[k].push_back(rc);
build(lc,l,mid),build(rc,mid+1,r);
}
void upd(int x,int y,int u,int k=1,int l=1,int r=n)
{
if(l>=x&&r<=y) {if(id[u]!=k) G[id[u]].push_back(k);return;}
if(x<=mid) upd(x,y,u,lc,l,mid);
if(mid<y) upd(x,y,u,rc,mid+1,r);
}
inline int rd()
{
int x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
int dn,top,cnt,stk[N],dfn[N],low[N],bel[N];
void tarjan(int u)
{
stk[++top]=u;
dfn[u]=low[u]=++dn;
for(int v:G[u])
{
if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
else if(!bel[v]) low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
int v;++cnt;
do{
v=stk[top--];
bel[v]=cnt;
if(rev[v]) l[cnt]=min(l[cnt],L[rev[v]]),r[cnt]=max(r[cnt],R[rev[v]]);
}while(v!=u);
}
}
void dfs(int u)
{
vis[u]=1;
for(int v:g[u])
{
if(!vis[v]) dfs(v);
l[u]=min(l[u],l[v]);
r[u]=max(r[u],r[v]);
}
}
signed main()
{
n=rd();build();
memset(l,0x3f,sizeof(l));
for(int i=1;i<=n;i++) x[i]=rd(),y[i]=rd();
for(int i=1;i<=n;i++)
{
L[i]=lower_bound(x+1,x+1+n,x[i]-y[i])-x;
R[i]=upper_bound(x+1,x+1+n,x[i]+y[i])-x-1;
upd(L[i],R[i],i);
}
tarjan(1);
for(int i=1;i<=tot;i++) for(int j:G[i]) if(bel[i]!=bel[j]) g[bel[i]].push_back(bel[j]);
for(int i=1;i<=cnt;i++) if(!vis[i]) dfs(i);
for(int i=1;i<=n;i++) ans=(ans+1ll*i*(r[bel[id[i]]]-l[bel[id[i]]]+1))%P;
cout<<ans<<'\n';
}