本来是不想写这篇博客的,但为了课前十分钟还是来水一发
前缀和
简介
继续引用OI-Wiki的话(OI-Wiki $yyds$ !):
前缀和可以简单理解为「数列的前 $n$ 项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
也就是说,我们能使用 $O(n)$ 的时间进行预处理,在 $O(1)$ 的时间内求出数列的一段区间内所有数的和。
为什么要使用前缀和?
假如我们有一段长为 $1e6$ 的数列,有 $1e6$ 个询问,假如我们使用传统的方式,对每一个询问以一个一个相加的方式进行求和,那么最坏情况下这个程序要运行 $1e12$ 次,妥妥的 $TLE$ 。但是我们使用前缀和的话就可以免去这些操作了。
那么怎么做?
假设给出的数列为 $a$ ,我们可以构造出一个相应的数列 $sum$ ,其中第 $x$ 个元素的值为 $a$ 数列中 $1$ ~ $x$ 个元素的和,即:$ sum_x = \sum\limits_{i = 1} ^ x a_i$ 。
那么显然,如果我们要求出从第 $l$ 个元素到第 $r$ 个元素,只要求出 $sum_r - sum_{l - 1}$ 的值就可以了。
而 $sum$ 数列中每一个元素的值,我们可以用前一个元素的值加上 $a$ 数列中对应位置元素的值求的。特别地,$sum$ 数列中第一个元素的值就等于 $a$ 数列中第一个元素的值。
示范代码如下:
cin >> n >> q;
for (int i = 1; i <= n; i++){
cin >> a[i];
sum[i] = a[i] + sum[i - 1];
}
while(q--){
cin >> l >> r;
cout << sum[r] - sum[l - 1] << endl;
}
扩展:二维前缀和
前面我们的讨论都是在一个一位的数列上进行的,但如果题目给我们的是一个二维的矩阵,阁下又当如何应对?
显然的,我们同样可以构造一个矩阵 $sum$ 使得 $sum_{x, y} = \sum\limits_{i = 1} ^ x \sum\limits_{j = 1} ^ y a_{i, j}$ 。怎么求出 $sum_{x, y}$ 的值呢?
首先,我们要加上 $a_{x, y}$ 的值。然后根据容斥原理,我们会重复加上一部分的前缀和,于是需要减去一部分。
如下图所示。我们要计算整块前缀和,就要先加上右下角这些,再加上左侧的所有前缀和和上面的前缀和。这时你会发现,我们把左上角的那一部分算了两次,于是我们减掉一次就好了。

那么怎么查询特定块的前缀和呢?
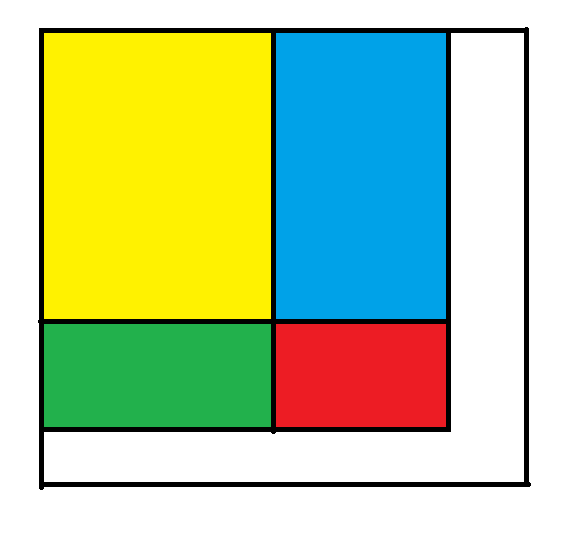
再看下面这张图。我们现在要计算红色部分的前缀和,而红色部分的前缀和等于总的前缀和 $-$ 它正上方的前缀和(蓝色部分) $-$ 它左侧的前缀和(绿色部分) $-$ 它左上方的前缀和(黄色部分)。根据二位前缀和的定义,我们可以求得它左侧和左上方的总前缀和(绿色和黄色部分),它正上方和左上方的总前缀和(蓝色和黄色部分)。再次根据容斥原理,我们两次减去了黄色部分,应该加回一次。这就是红色部分的前缀和。
下面是示范代码:
// 处理前缀和
cin >> n >> m >> q;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> a[i][j];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
// 查询前缀和
while(q --){
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
cout << sum[l2][r2] - sum[l1 - 1][r2] - sum[l2][r1 - 1] + sum[l1 - 1][r1 - 1] << endl;
}
差分
简介
再次引用OI-Wiki的话:
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
用人话来说,差分支持我们通过前缀和的方式,实现 $O(1)$ 对一个数列中一段区间元素的值进行修改,并且方便的得到每一个值。
为什么要使用差分
同理,使用差分可以避免对数列中每个元素的值一个一个进行修改,使得程序的运行时间大大减少。
那么怎么做?
针对给出的数列 $a$ ,我们可以构造出一个数列 $b$ ,使得其中每一个元素的值都是 $a$ 数列中对应元素的值减去前一个元素的值,也就是 $b_i = a_i - a_{i - 1}$
那么我们可以得出这样的一个式子:$a_x = \sum\limits_{i = 1} ^ x b_i$。很显然,我们可以利用前缀和求出 $a$ 中元素的值。
但这样显然没有任何优势,但是差分的优势在于对区间元素的修改。假如我们要给 $l$ 到 $r$ 之间的元素都加上一个值 $val$ ,我们只需要给 $b_l$ 的值加上 $val$ ,给 $b_{r + 1}$ 的值减去 $val$ 就可以了。
解释以下。根据差分的定义,给 $b_l$ 的值加上 $val$ 就相当于给 $a_l$ 到数列末尾元素的值都加上 $val$ ,那么给 $b_{r + 1}$ 减去 $val$ 就可以抵消其对于 $a_{r + 1}$ 到数列末尾的影响了。
示范代码如下:
cin >> n >> q;
for (int i = 1; i <= n; i++){
cin >> a[i];
b[i] = a[i] - a[i - 1];
}
while(q--){
cin >> l >> r >> val;
b[l] += val;
b[r + 1] -= val;
}
for (int i = 1; i <= n; i++){
sum[i] = sum[i - 1] + b[i];
cout << sum[i] << ' ';
}