【笔记】曼哈顿距离与切比雪夫距离的互化

图源：https://www.cnblogs.com/SGCollin/p/9636955.html

曼哈顿距离：\(|x_a - x_b| + |y_a - y_b|\)

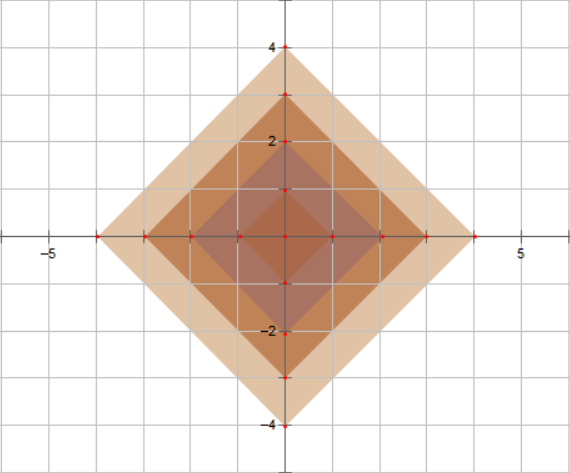
切比雪夫距离：\(\max(|x_a - x_b|,|y_a - y_b|)\)

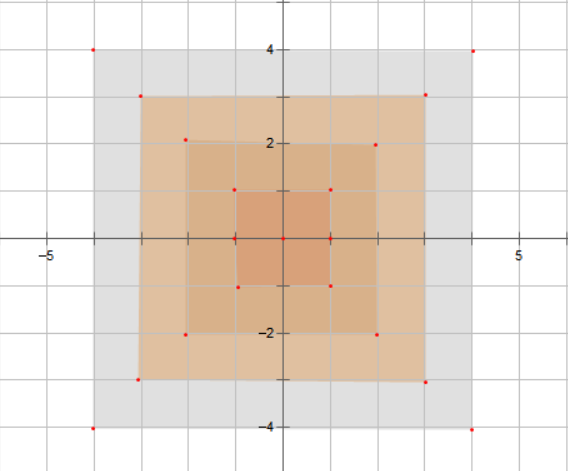
在有的题目中，要求是一种距离，但使用另一种距离更加方便。比如曼哈顿距离就可以将两维拆开来考虑，所以很多情况会有切比雪夫距离转曼哈顿距离的 trick。

观察图片，设 \(A(x_a, y_a), B(x_b, y_b)\)，则：

• \(A,B\) 的曼哈顿距离等于 \((x_a + y_a, x_a - y_a), (x_b + y_b, x_b - y_b)\) 两点的切比雪夫距离。

\((x,y)\to(x+y, x-y)\)。

• \(A,B\) 的切比雪夫距离等于 \((\frac{x_a + y_a}2, \frac{x_a - y_a}2), (\frac{x_b + y_b}2, \frac{x_b - y_b}2)\) 两点的切比雪夫距离。

\((x,y)\to(\dfrac{x+y}2, \dfrac{x-y}2)\)。

例题：

POI2006 - MAG-Warehouse : https://www.luogu.com.cn/problem/P3439。
TJOI2013 - 松鼠聚会 : https://www.luogu.com.cn/problem/P3964。
ABC221G - Jumping sequence : https://www.luogu.com.cn/problem/AT_abc221_g