定义
顾名思义,就是说在 DP 取最值的过程中选的转移点 \(j\) 是单调的。只要有这个性质,就可以优化枚举转移的复杂度。
充要条件
\[f_i=\text{最值}(g_j+w(j+1,i)) \]\(w\) 满足四边形不等式。
这里以取 \(\min\) 为例。假设有决策点 \(j_1<j_2\),\(w\) 满足四边形不等式等价于 \(\Delta w(j_1)\ge \Delta w(j_2)\),这样才能让它一直是单调的。只要把 \(\Delta w\) 转换成两个 \(w\) 相减就可以得到式子 \(w(j_1,i_2)-w(j_1,i_1)\ge w(j_2,i_2)-w(j_2,i_1),j_1<j_2<i_1<i_2\),再移项就是 \(w(j_1,i_1)+w(j_2,i_2)\le w(j_1,i_2)+w(j_2,i_1)\)。即 \(\text{交叉}\le\text{包含}\)。
以上三种形式,只要可以验证(指暴力)某一个,即可认为 \(w\) 满足四边形不等式。
推导决策单调性
反证法,设 \(f_{i1}\leftarrow f_{j2},f_{i2}\leftarrow f_{j1}\),可以得到:
\[\begin{cases} f_{j2}+w(j2,i1)\le f_{j1}+w(j1,i1)\hspace{2.5cm}1\\ f_{j2}+w(j2,i2)\ge f_{j1}+w(j1,i2)\\ w(j_1,i_1)+w(j_2,i_2)\le w(j_1,i_2)+w(j_2,i_1)\hspace{1cm}2 \end{cases} \]1 式加 2 式得:
\[\begin{cases} f_{j2}+w(j2,i2)\le f_{j1}+w(j1,i2)\\ f_{j2}+w(j2,i2)\ge f_{j1}+w(j1,i2) \end{cases} \]矛盾。
应用
当 \(g_j\) 与 \(f_j\) 无关时,直接整体二分。
否则,转化一下。决策点单调等价于每个决策点被转移到的集合是连续区间且单调。
当 \(\text{交叉}\le\text{包含}\) 时,有这样的图像(y 轴应为 \(f_j+w(j,i)\)):
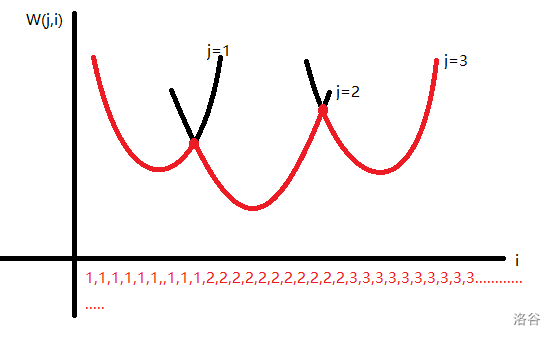
求 \(\min\) 维护红色,用单调队列加二分;求 \(\max\) 维护黑色,单调栈+二分。
\(\text{交叉}\ge\text{包含}\) 时反之。
推广
满足四边形不等式和 \(w(j1,i2)\le w(j2,i1)\) 后,同样可以优化区间 DP、前 \(i\) 分 \(j\) 段的 DP。
标签:le,text,i2,决策,j2,j1,单调 From: https://www.cnblogs.com/mRXxy0o0/p/17827011.html