格路径计数
基础格路径计数
问题:格路径上从 \((0,0)\) 走到 \((n,m)\) 只能向上或向右走,方案数。
显然一共走 \(n+m\) 次,选出任意 \(n\) 次向上走方案数就是 \(\binom {n+m} n\)。
有限制格路径计数
下面说的限制都是不接触到某条线的限制,若题目要求不超过,可以依次 \(+1/-1\)。
单条直线限制
还是从 \((0,0)\) 走到 \((n,m)\),但在格路径上你不能经过 \(y=x+k\) 这条直线,求方案数。
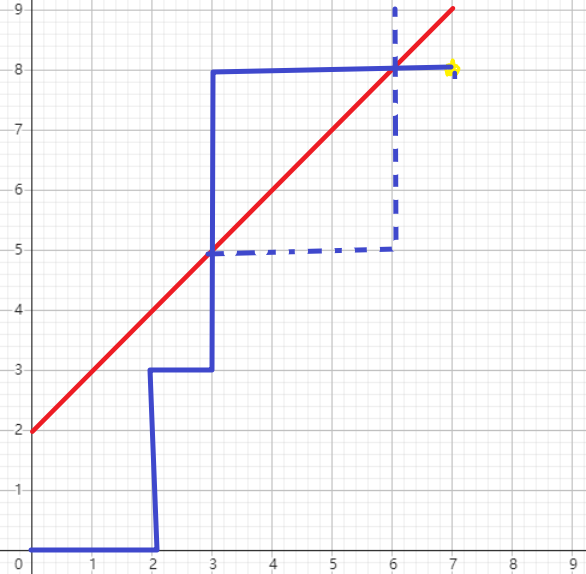
这是卡特兰数经典问题,考虑把最后一次进入直线之后的路径后半部分翻折一下,最终终点也会翻折变成 \((m-k, n+k)\),总方案 \(\binom {n+m} n\) 减去不合法的部分 \(\binom {n+m} {n+k}\) 就是
\[\binom {n+m} n - \binom {n+m} {n+k} \]两条直线限制
还是从 \((0,0)\) 走到 \((n,m)\),但在格路径上你不能经过 \(y=x+k_1,y=x+k_2,(k_1>0,k_2<0)\) 这两条直线,求方案数。
有人说直接对两条直线分别做然后减去就行了。
但遇到一个路径同时经过两条直线的情况就会算重复。

我们设两条直线分别为 A,B,我们定义一个 AB 字符串例如 BABA 表示依次进入直线 BABA ,若多次进入 A 或 B,只考虑第一次,也就是 ABBBAAAABBB = ABAB。
我们设 \(f_{\texttt{ABAB}}\) 表示终点 \((n,m)\) 依次对 BABA 直线进行对称得到的新终点 \((n',m')\) ,然后\((0,0)\) 到新终点 \((n',m')\) 的无限制方案数。
对于一个路径序列代表的字符串 ABABA,我们把字符串每一个本质不同的子段在最后一次出现的位置倒着依次翻折,这样和 \(f\) 中的方案数一一对应。
例如 ABABA 的子段 ABA,我们在最后一次进入 A 时翻折一下,最后一次进入 B 时翻折一下,倒数第二次进入 A 时再翻折一下。(如下图,三种颜色代表三次不同翻折)
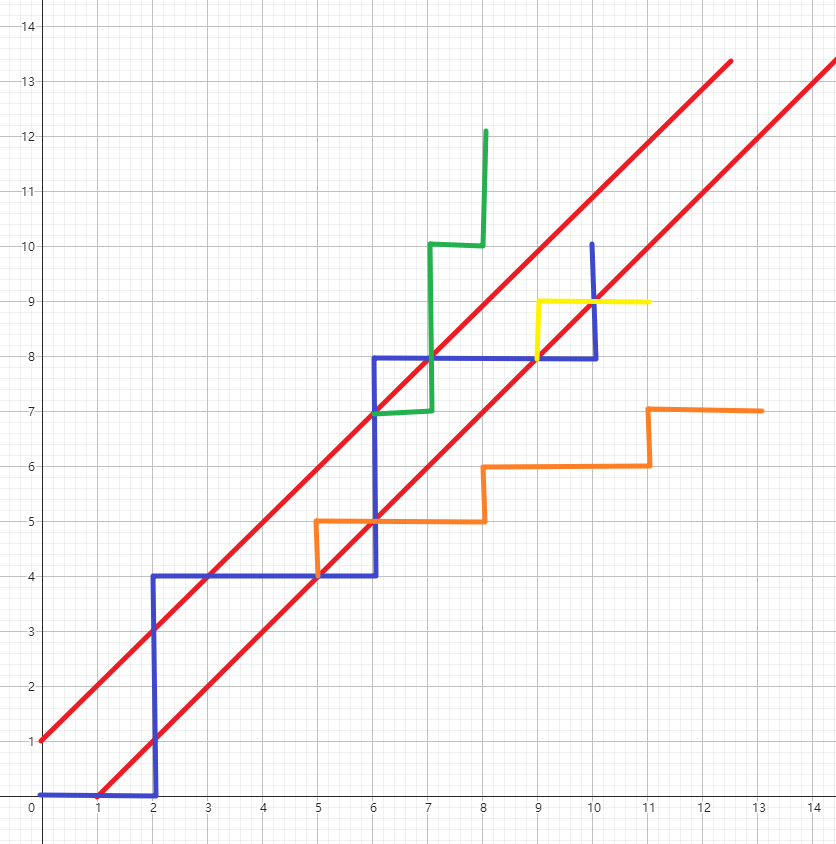
我们发现序列 \(ABABA\) 会贡献到 \(f_{\text{A}},f_{\text{B}},f_{\text{AB}},f_{\text{BA}},f_{\text{ABA}},f_{\text{BAB}},f_{\text{ABAB}},f_{\text{BABA}},f_{\text{ABABA}}\),并且贡献都是 1 。
贡献都是 1 是因为我们只翻折最后一次出现的位置,大家可以手模一下发现若翻折前面出现的位置得出的路径和原来的不一样。
于是不合法的方案数就变成了:
\[f_{\text{A}} + f_{\text{B}} - f_{\text{AB}} - f_{\text{BA}} + f_{\text{ABA}} + f_{\text{BAB}} - ... \]会发现这样每条直线只会被计算一次。
总方案 \(\binom{n+m}{n}\) - 不合法方案数就可以了。
多条直线限制
可以找出限制最紧的两条变成两条直线限制。
k-Dyck路(k阶卡特兰数)
问题:还是格路径,但是现在只能向上走 \(k\) 格或向右走 \(1\) 格,不超过 \(y=x\) (不接触 \(y=x+1\))求 \((0,0)\) 到 \((nk, nk)\) 方案数。
这是 \(k = 2\) 时的某种合法方案。

我们我们转化为一个新问题:
只能向上走 \(k\) 格或向右走 \(1\) 格, 从 \((0,0)\) 到 \((nk+1, nk)\) 的方案数,没有限制。
向上走的数量为 \(n\),向右走的数量为 \(nk+1\),一共 \(n(k+1) + 1\) 次,方案数显然是:
\[\binom {n(k+1)+1} n \]我们将新问题中的接触到 \(y=x\) 的路径进行一个转变,转变方式如下:
首先找出在直线 \(y=x\) 上方的所有点(包括在 \(y=x\) 上的点),选择一个距离 \(y=x\) 最远的点(若有多个点距离相同,选择距离终点最近的点),称之最高点。
将最高点后边的路径平移到 \((0,0)\),将之前从 \((0,0)\) 开始的路径接到后面。
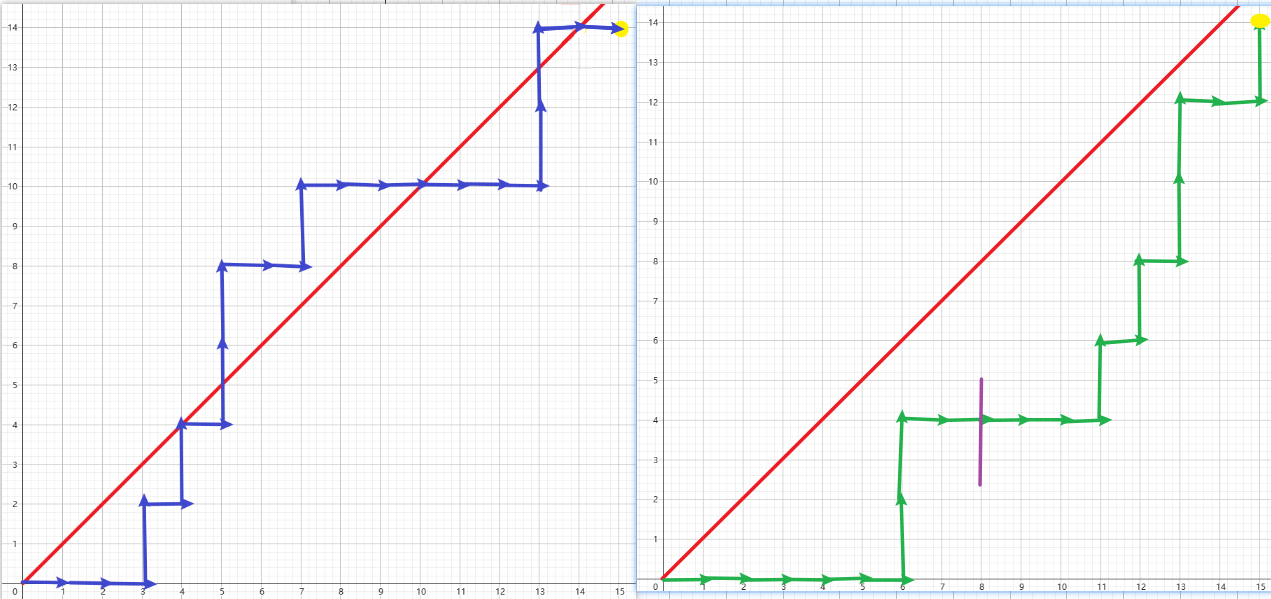
可以证明,转变之后的新路径满足一下几个性质:
-
一定不会接触到 \(y=x\)。
- 这里很显然。
-
最开始一定有两次向右操作。
-
当找出的最高点不在 \(y=x\) 上,设向右和向上分别为 \(R,U\),若这个点之后的操作为 \(U\) 或者 \(RU\),那么在操作后的点一定距离 \(y=x\) 更远,最高点会选择他。
-
当最高点在 \(y=x\) 上时,他只有两种可能:
-
第一种和上面那种一样。
-
第二种是下一步只需要一次 \(R\) 就可以到终点,若是这种情况,那么旧路径的第一次操作一定是 \(R\),否则就会出现一个点在 \(y=x\) 上方,最高点不会选到它。
-
-
我们删去新路径的第一次 \(R\) 操作,终点变成了 \((nk,nk)\),限制变成了不超过 \(y=x\) (不接触 \(y=x+1\)),会发现和旧问题中的路径一一对应。
新问题的新路径和旧问题路径一一对应,但新问题的旧路径和新问题的新路径并不是一一对应的。
我们发现在新路径中将任意一断点截断,交换两个部分(上述转变的逆过程),本身的终点会在操作后变成最高点,且均在 \(y=x\) 上及其上方。
这样每一种旧路径对应一个新路径,每一个新路径对应 \(n(k+1)+1\) 旧路径,答案就是:
\[\frac{1}{n(k+1)+1}\binom {n(k+1)+1} n \] 标签:直线,翻折,text,路径,计数,nk,binom From: https://www.cnblogs.com/hfjh/p/17823806.html