RE:从零开始的计算几何生活
爱来自 yyc。
定义一些坏文明:
#define db double
const db eps = 1e-10;
误差计算:
int sign (double x) {
return x > eps ? 1 : (x < -eps ? -1 : 0);
}
向量:
struct vec {
double x, y;
void debug () { printf("%.3lf %.3lf\n", x, y); }
vec operator + (const vec & t) const { return vec{x + t.x, y + t.y}; }
vec operator - (const vec & t) const { return vec{x - t.x, y - t.y}; }
vec operator * (const double & t) const { return vec{x * t, y * t}; }
vec operator / (const double & t) const { return vec{x / t, y / t};}
double len () { return sqrt(x * x + y * y); }
double operator | (const vec & t) const {
return x * t.x + y * t.y;
}
double operator ^ (const vec & t) const {
return x * t.y - y * t.x;
}
} ;
数量积:
double operator | (const vec & t) const {
return x * t.x + y * t.y;
}
叉积:
double operator ^ (const vec & t) const {
return x * t.y - y * t.x;
}
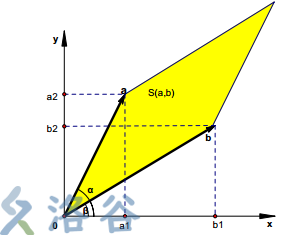
几何意义是两个向量围成的平行四边形的有向面积。如果是正的那么 \(\vec{b}\) 是 \(\vec{a}\) 逆时针转过来的,那么 \(\vec{a} \times \vec{b} = a.x * b.y - a.y * b.x\) 。
乐。
凸包
按照水平顺序排序。
考虑增量构造法。
怎样一个点才会被加入凸包。那么如果加入一个点的时候,可以包住以前的点显然才会加入凸包。
所以使用单调栈维护栈顶和栈顶底下的点就可以维护一个凸包乐。
如果成乐顺时针夹角,那么就弹掉栈顶加点。这样必然可以求得下凸壳。
乐。
通过!
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; i ++)
#define per(i, r, l) for (int i = r; i >= l; i --)
#define db double
using namespace std;
typedef long long ll;
const int _ = 1e5 + 5, mod = 998244353;
const db eps = 1e-10;
int n, stk[_], top;
int sign (double x) {
return x > eps ? 1 : (x < -eps ? -1 : 0);
}
struct vec {
double x, y;
void debug () { printf("%.3lf %.3lf\n", x, y); }
vec operator + (const vec & t) const { return vec{x + t.x, y + t.y}; }
vec operator - (const vec & t) const { return vec{x - t.x, y - t.y}; }
vec operator * (const double & t) const { return vec{x * t, y * t}; }
vec operator / (const double & t) const { return vec{x / t, y / t};}
double len () { return sqrt(x * x + y * y); }
double operator | (const vec & t) const {
return x * t.x + y * t.y;
}
double operator ^ (const vec & t) const {
return x * t.y - y * t.x;
}
bool operator == (const vec & t) { return !sign(x - t.x) && !sign(y - t.y); }
} p[_];
bool cmp (vec a, vec b) { return sign(a.x - b.x) == 0 ? a.y < b.y : a.x < b.x; }
double dis (vec x, vec y) {
vec z = x - y;
return z.len();
}
bool antilock (vec x, vec y, vec z) { return sign((x - z) ^ (y - z)) >= 0; }
int main() {
/*
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
黛拉可玛莉·岗德森布莱德,一亿年一遇美少女。
*/
cin >> n;
rep(i, 1, n) scanf("%lf%lf", & p[i].x, & p[i].y);
sort(p + 1, p + 1 + n, cmp);
n = unique(p + 1, p + 1 + n) - (p + 1);
stk[1] = 1, stk[top = 2] = 2;
rep(i, 3, n) {
while(top >= 2 && !antilock(p[i], p[stk[top]], p[stk[top - 1]]))
top --;
stk[++ top] = i;
}
double ret = 0;
rep(i, 1, top - 1) ret += dis(p[stk[i]], p[stk[i + 1]]);
stk[1] = n, stk[top = 2] = n - 1;
per(i, n - 2, 1) {
while(top >= 2 && !antilock(p[i], p[stk[top]], p[stk[top - 1]]))
top --;
stk[++ top] = i;
}
rep(i, 1, top - 1) ret += dis(p[stk[i]], p[stk[i + 1]]);
printf("%.2lf", ret);
return 0;
}
旋转卡壳
凸包内最远点对 \(\to\) 直径
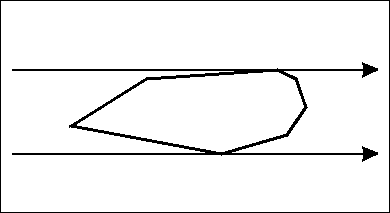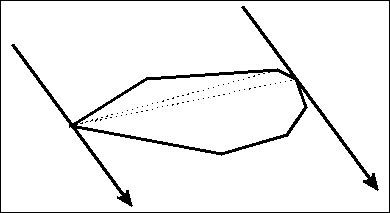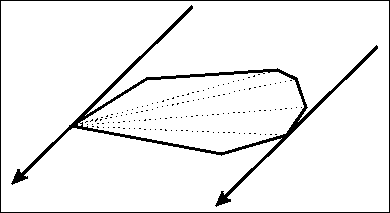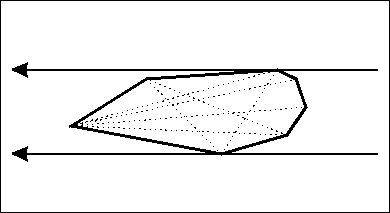
定义凸包上的对踵点对 : 用两条平行直线卡着凸包转,着两条直线一定会卡住至少两个点,这两个点称为对踵点对。
旋 转 卡 壳。
引理(重要) : 只用考虑斜率恰好与凸包某条边相同的直线。
证明:感觉证明法。
考虑最远点也是随着边旋转的,所以边走边跑双指针即可。
注意维护点到直线的距离,可以使用叉积加面积法解决,但是这里固定乐一个边。
注意不能保留共线点即可。
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; i ++)
#define per(i, r, l) for (int i = r; i >= l; i --)
#define db double
using namespace std;
typedef long long ll;
const int _ = 1e5 + 5, mod = 998244353;
const db eps = 1e-7;
int n, stk[_], top;
int sign (double x) {
return x > eps ? 1 : (x < -eps ? -1 : 0);
}
struct vec {
double x, y;
void debug () { printf("%.3lf %.3lf\n", x, y); }
vec operator + (const vec & t) const { return vec{x + t.x, y + t.y}; }
vec operator - (const vec & t) const { return vec{x - t.x, y - t.y}; }
vec operator * (const double & t) const { return vec{x * t, y * t}; }
vec operator / (const double & t) const { return vec{x / t, y / t};}
double len () { return sqrt(x * x + y * y); }
double operator | (const vec & t) const {
return x * t.x + y * t.y;
}
double operator ^ (const vec & t) const {
return x * t.y - y * t.x;
}
bool operator == (const vec & t) { return !sign(x - t.x) && !sign(y - t.y); }
} p[_];
bool cmp (vec a, vec b) { return sign(a.x - b.x) == 0 ? a.y < b.y : a.x < b.x; }
double dis (vec x, vec y) {
vec z = x - y;
return z.len();
}
bool antilock (vec x, vec y, vec z) { return sign((x - z) ^ (y - z)) > 0; }
double su (vec x, vec y, vec z) { return abs((x - y) ^ (x - z)); }
int tot;
vec v[_];
void hull () {
rep(i, 1, n) scanf("%lf%lf", & p[i].x, & p[i].y);
sort(p + 1, p + 1 + n, cmp);
stk[1] = 1, stk[top = 2] = 2;
rep(i, 3, n) {
while(top >= 2 && !antilock(p[i], p[stk[top]], p[stk[top - 1]]))
top --;
stk[++ top] = i;
}
rep(i, 1, top) v[++ tot] = p[stk[i]];
stk[1] = n, stk[top = 2] = n - 1;
per(i, n - 2, 1) {
while(top >= 2 && !antilock(p[i], p[stk[top]], p[stk[top - 1]]))
top --;
stk[++ top] = i;
}
rep(i, 2, top - 1) v[++ tot] = p[stk[i]];
}
double RotateHull () {
double ans = 0;
if (tot == 2) { ans = dis(v[1], v[2]); return ans; }
v[0] = v[tot];
int cur = 2;
rep(i, 1, tot) {
while(su(v[cur % tot + 1], v[i], v[i - 1]) > eps + su(v[cur], v[i], v[i - 1]))
cur = cur % tot + 1;
ans = max(ans, dis(v[cur], v[i]));
ans = max(ans, dis(v[cur], v[i - 1]));
}
return ans;
}
int main() {
/*
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
黛拉可玛莉·岗德森布莱德,一亿年一遇美少女。
*/
cin >> n;
hull();
double diameter = RotateHull();
printf("%.0lf", diameter);
return 0;
}
闵可夫斯基和
\(\{a + b | a \in A, b \in B \}\)
具体来说就是把 \(B\) 中的每个点当成向量,沿着这个走所到达的所有点集。
乐。
凸壳的话,两个凸壳的闵可夫斯基和是凸壳。
结论 : 将两个凸包上的边按照极角序顺次连接即可得到答案。
「JSOI2018战争」
题面略去。
考虑求 \(B\) 和 \(-A\) 的闵可夫斯基和,判定是不是在 \(x\) 上即可。
半平面交
乐。
标签:return,double,top,stk,RE,从零开始,vec,几何,const From: https://www.cnblogs.com/Custlo/p/17822995.html