P3217 [HNOI2011] 数矩形题解

前言

提交记录

本题其实并不是非常难想，那么为什么本蒟蒻还交了那么多发呢？

cal 函数求平方的时候传值未开 long long ，我谔谔。

正文

题面省流：给定 $n$ 个点求最大举行的面积，矩形的边可以不与坐标系垂直。

如果每次枚举矩形的四个点的话，$O\left(n^4\right)$ 可以得到 $20%$ 的美妙暴力分。

看看正解？

要求矩形我们可以利用一些优美的数学性质：

矩形的对角线相等且互相平分。

也就是说我们可以枚举对角线，判断它们的中点是否重合，长度是否相等。

在 n<=1500 的情况下可O(n^4)枚举所有对角线，然后排序，排序主要关键字为坐标，次要关键字为权值。

对角线数量有n*(n-1)/2条，相当于O(n^2)遍历对角线，任意两条中点相同并且长度相同的对角线均计算其组成矩形面积并更新最大值。

一张图解决如何求面积：

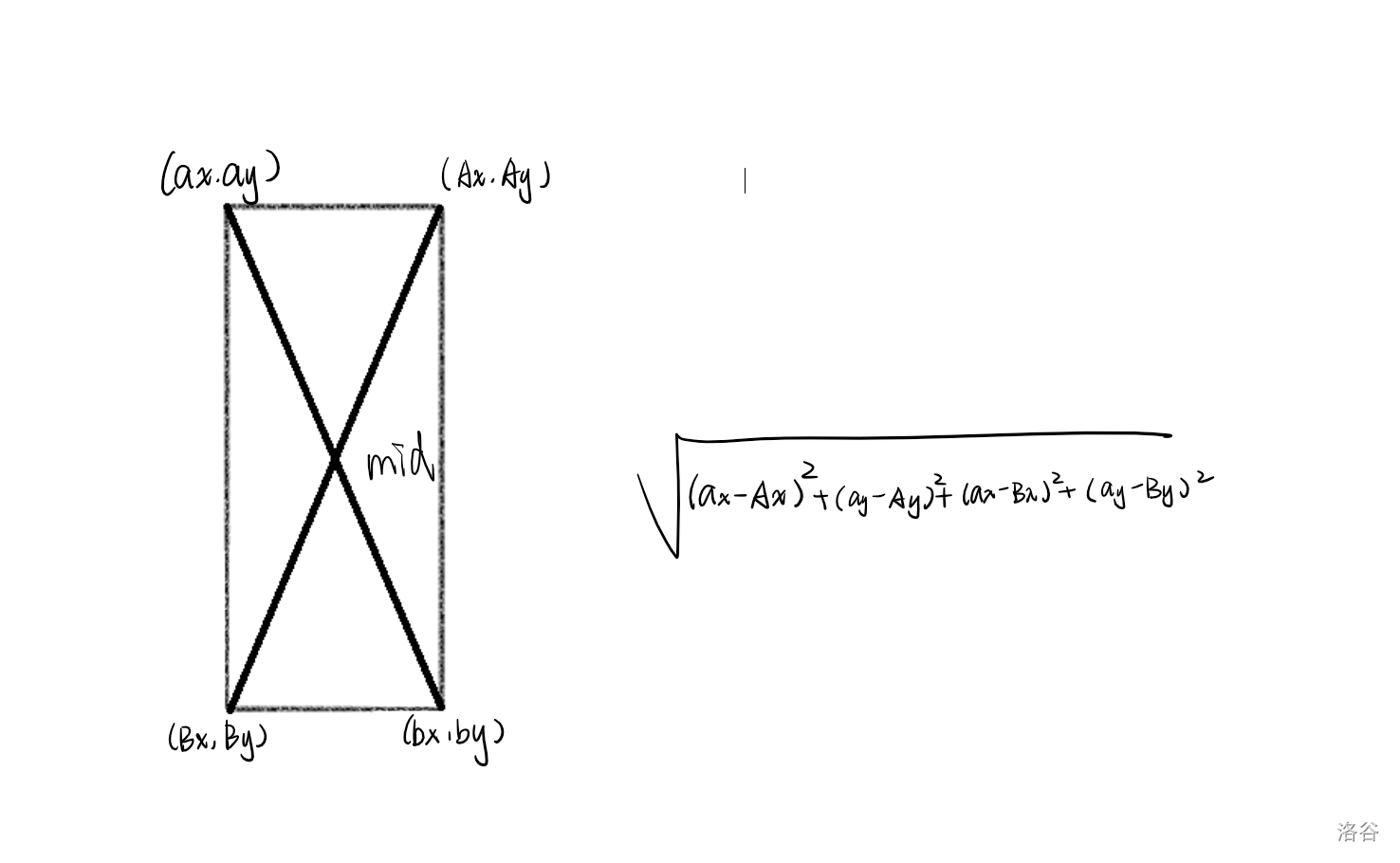
贴码

#include<bits/stdc++.h>
#define MAXN 1510
using namespace std;
//ifstream is("num.in",ios::in);
//ofstream os("num.out",ios::out);
//#define cin is
//#define cout os
long long n,x[MAXN],y[MAXN],tote;
long long ans=0;
struct Edge{
	long long onex,oney,twox,twoy;
	long long midx,midy;
	long long dist;
}e[MAXN*MAXN];
bool cmp(Edge x,Edge y){
	if(x.midx==y.midx){
		if(x.midy==y.midy) return x.dist<y.dist;
		return x.midy<y.midy;
	}
	return x.midx<y.midx;
}
inline long long cal(long long x){
	return x*x;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>x[i]>>y[i];
	for(int i=1;i<=n;i++){
		for(int j=1+i;j<=n;j++){
			e[++tote].onex=x[i]; e[tote].oney=y[i];
			e[tote].twox=x[j]; e[tote].twoy=y[j];
			e[tote].midx=x[i]+x[j];
			e[tote].midy=y[i]+y[j];
			e[tote].dist=cal(x[i]-x[j])+cal(y[i]-y[j]);
		}
	}
	sort(e+1,e+tote+1,cmp);
	int st=0;
	for(int i=1;i<=tote;i++){
		if(e[i].midx==e[st].midx&&e[i].midy==e[st].midy){
			for(int j=st;j<=i;j++){
				if(e[i].dist==e[j].dist)
				ans=max(ans,(long long)(sqrt( cal(abs(e[i].onex-e[j].onex))+cal(abs(e[i].oney-e[j].oney)) )*sqrt( cal(abs(e[i].onex-e[j].twox) ) + cal(abs(e[i].oney-e[j].twoy) ) )));
			}
		}
		else if(e[i].midx!=e[st].midx||e[i].midy!=e[st].midy)st=i;
	} 
	cout<<ans;
	return 0;
}
/*
点个赞吧谢谢喵~
8
-2 3
-2 -1
0 3
0 -1
1 -1
2 1 
-3 1 
-2 1
*/