可持久化线段树
前置知识:
- 动态开点线段树
基本介绍
可持久化线段树可以维护多个版本信息。
举个例子:
你需要维护这样的一个长度为 \(N\ (1\le n\le 10^6)\) 的数组,支持如下几种操作
- 在某个历史版本上修改某一个位置上的值
- 访问某个历史版本上的某一位置的值
每次操作后生成一个新的版本。
(就是板子1)
考虑使用线段树,开多个线段树,每次操作复制一遍,但是这样会爆。
我们发现,线段树上每次操作最多只有 \(log(n)\) 个节点被改变,所以我们每次修改时,对于未被改变的节点,直接指向先前版本的节点。
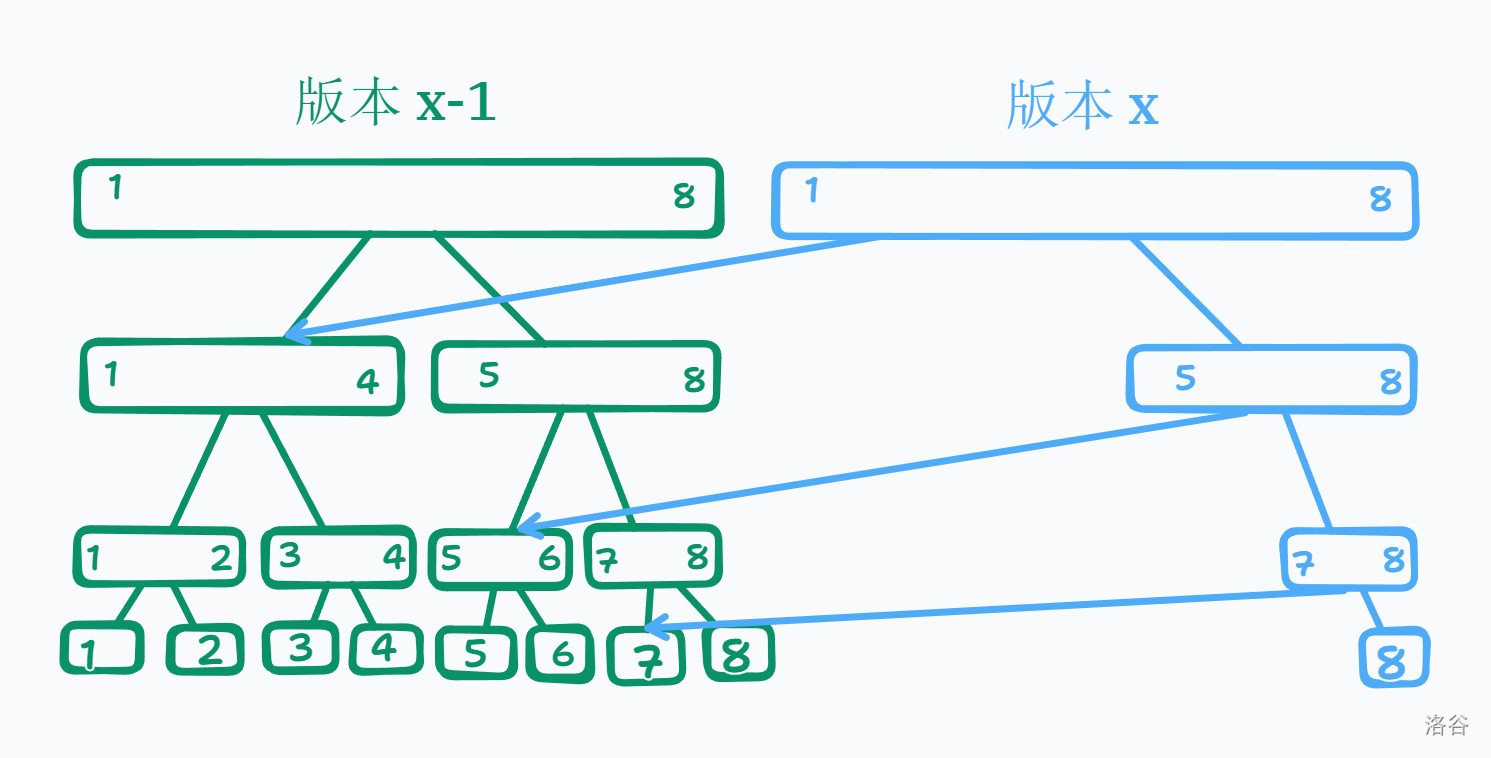
如上图,我们以 版本 \(x-1\) 为基础,将第 \(8\) 个元素修改,并创建一个新的版本 \(x\) 。对于未被修改的节点 \([1,4],[5,6],[7,7]\) 我们直接指向 版本 \(x-1\) 的对应节点,被修改的节点 \([1,8],[5,8],[7,8],[8,8]\) 需要创建。
可持久化线段树一般为单点修改,区间修改可以用标记永久化(但是我不会)。数组要开到 Max<<5 左右
板子1代码
点击查看代码
#include <iostream>
#define int long long
const int M = 1e6+10;
int n,m,a[M],root[M],cnt,tot;
struct Tree
{
int ls,rs,num;
}t[M<<5];
void build(int x,int l,int r)
{
if(l==r){
t[x].num=a[l];
return ;
}
int mid=(l+r)>>1;
build(t[x].ls=++cnt,l,mid);
build(t[x].rs=++cnt,mid+1,r);
return ;
}
void change(int p,int q,int l,int r,int x,int y,int num)
{
if(l>=x&&r<=y){
t[q].num=num;
return ;
}
t[q].ls=t[p].ls,t[q].rs=t[p].rs;
int mid=(l+r)>>1;
if(mid >= x) change(t[p].ls,t[q].ls=++cnt,l,mid,x,y,num);
if(mid < y) change(t[p].rs,t[q].rs=++cnt,mid+1,r,x,y,num);
return ;
}
int getNum(int q,int l,int r,int x,int y)
{
if(l>=x&&r<=y)
return t[q].num;
int mid=(l+r)>>1;
if(mid >= x) return getNum(t[q].ls,l,mid,x,y);
if(mid < y) return getNum(t[q].rs,mid+1,r,x,y);
}
inline int read(){
int num=0,fl=1;char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') fl=-1;
c=getchar();
}
while(c >='0'&&c <='9'){
num=(num<<3)+(num<<1)+(c^48);
c=getchar();
}
return num*fl;
}
signed main(){
n=read(),m=read();
for(int i = 1;i<=n;i++)a[i]=read();
build(root[0]=++cnt,1,n);
while(m--){
int v=read(),mod=read();
if(mod==1){
int x=read(),num=read();
change(root[v],root[++tot]=++cnt,1,n,x,x,num);
}
if(mod==2){
int x=read();
printf("%lld\n",getNum(root[v],1,n,x,x));
root[++tot]=root[v];
}
}
return 0;
}
静态区间 \(k\) 小值
可持久化线段树的第二种经典用法:查询区间的第 \(k\) 小个数。(板子2)
这里似乎就是主席树了(可持久化权值线段树)。
序列中的每个位置作为一个版本,维护当前位置前面(包括当前位置)所有元素的出现次数。(即节点 \([x,y]\) 表示 \(x\le a_i\le y\) 的数量) 。然后就可以通过差分得出 \([l,r]\) 区间内的元素的出现数量。最后考虑在线段树里二分,若左节点的值大于 \(k\) 则向左节点递归,否则将 \(k\) 减去左节点的值向右节点递归。
板子2代码
点击查看代码
#include <iostream>
#include <queue>
#include <vector>
#define int long long
const int M = 2e5+10;
const int inf = 1e9;
int n,m;
int a[M];
int root[M],cnt,tot;
struct Tree
{
int ls,rs,cnt;
}t[M<<5];
inline void pushUp(int x){t[x].cnt=t[t[x].ls].cnt+t[t[x].rs].cnt;}
void change(int p,int q,int x,int y,int l,int r)
{
if(l >= x&&r <= y){
t[q].cnt=t[p].cnt+1;
return ;
}
t[q].ls=t[p].ls,t[q].rs=t[p].rs;
int mid=(l+r)>>1;
if(mid >= x) change(t[p].ls,t[q].ls=++cnt,x,y,l,mid);
if(mid < y) change(t[p].rs,t[q].rs=++cnt,x,y,mid+1,r);
pushUp(q);
return ;
}
void Ans(int l,int r,int p,int q,int k)
{
if(l==r){
printf("%lld\n",l);
return;
}
int mid=(l+r)>>1;
if(k<=t[t[q].ls].cnt-t[t[p].ls].cnt) Ans(l,mid,t[p].ls,t[q].ls,k);
else Ans(mid+1,r,t[p].rs,t[q].rs,k-(t[t[q].ls].cnt-t[t[p].ls].cnt));
}
inline int read(){
int num=0,fl=1;char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') fl=-1;
c=getchar();
}
while(c >='0'&&c <='9'){
num=(num<<3)+(num<<1)+(c^48);
c=getchar();
}
return num*fl;
}
signed main(){
n=read(),m=read();
root[0]=++cnt;
for(int i = 1;i <= n;i++){
a[i]=read();
change(root[i-1],root[i]=++cnt,a[i],a[i],-inf,inf);
}
while(m--){
int l=read(),r=read(),k=read();
Ans(-inf,inf,root[l-1],root[r],k);
}
return 0;
}
一些其他题
跟区间第 \(k\) 小差不多。二分查 \(k\) 小值改成查 \(\dfrac{l+r}{2}\) 就行了。
标签:cnt,持久,int,线段,mid,笔记,ls,节点 From: https://www.cnblogs.com/cnm2k3h/p/17796199.html