卷积实现
\[y(n) = x(n) * h(n) \\ y(n) = \sum_{m = -\infin}^{\infin}x(m)h(n-m) \]%确定第一个序列的x轴和y轴坐标
nx = [0:1]; x = [1 2];
%确定第二个序列的x轴和y轴坐标
nh = [0:2]; h = [3 2 1];
%conv 是matlab自带的对两个序列进行卷积的函数
y = conv(x,h);
%注意配好完成卷积后结果的x轴坐标
ny = [0:3];
%画图
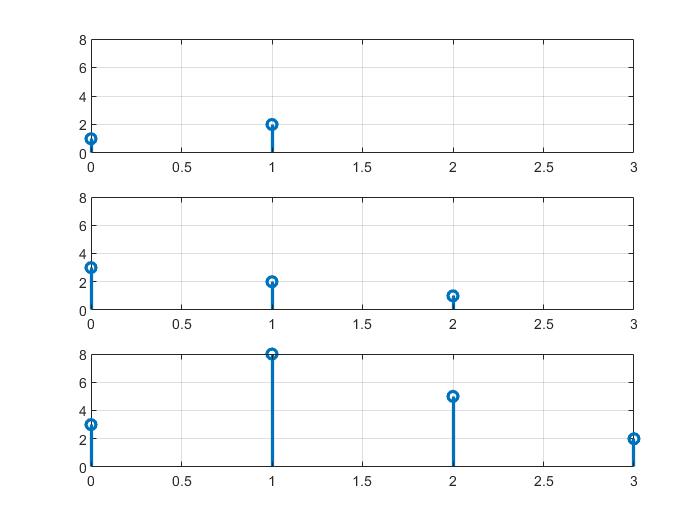
subplot(3,1,1); stem(nx,x,'linewidth',2);
%选择图像要显示的区域
axis([min(ny) max(ny) 0 max(y)] ); grid on;
subplot(3,1,2);stem(nh,h,'linewidth',2);
axis([min(ny) max(ny) 0 max(y)] ); grid on;
subplot(3,1,3); stem(ny,y,'linewidth',2);
axis([min(ny) max(ny) 0 max(y)] ); grid on;
互相关
\[r_{yx}(n)=y(n)*x(-n) \\ r_{yx}(n)=\sum_{m=-\infin}^{\infin}y(m)x(m-n) \]nx = [0:6]; x = [3,5,-7,2,-1,-3,2];
ny = [2:8]; y0 = x;
w = randn(1,length((y0))); %给y加上高斯噪声
y = y0+w;
ryx = xcorr(y,x); %互相关函数 xcorr
nryx = [-4:8]; %基本操作:运算后然后确定值得x轴范围
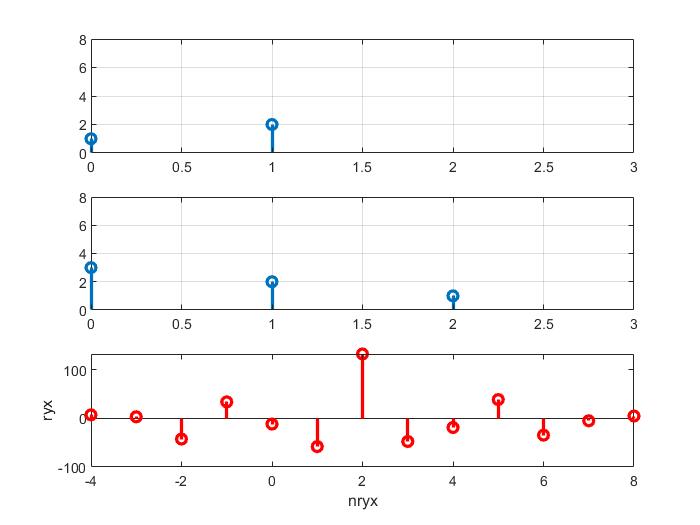
stem(nryx,ryx,'r','linewidth',2);%绘制图像
xlabel('nryx');ylabel('ryx');
差分方程的实现
\[\sum_{k=0}^N a_k y(n-k) = \sum_{m=0}^M b_mx(n-m) \]%函数形式:
y = filter(b,a,x)
%b为x序列系数,a为y序列系数,x为输入序列,y为输出序列
b = 0.5;a = [1 -0.5];
x = ones(1,100); %生成1x100个1
y = filter(b,a,x);%进行差分运算
plot(y);
