概率太尼玛有意思了, 啊哈哈哈.
\(Alex\_Wei\) 唱歌好听!
\(\text{【LOJ\#2834】「JOISC 2018 Day 2」修行}\)
\(\color{red}{\text{[HARD]}}\)
概率真好van, 这个世界真奇妙, 其实网上的题解大多写的不太对, 或者说没写明白, 当然也有写清楚了的, 所以 ljy orz , 让我弄清楚了这题.
首先还是一个经典的变换, 我们取 \(n\) 个随机变量 \(a_i\in [0,1)\) , 我们所求即为恰好有 \(k-1\) 个 \(a_i > a_{i+1}\) 的概率, 这等于满足要求的排列概率.
这里正确是因为我们只关注那 \(n-1\) 个是否为 \(0\) 或 \(1\) 并不关注具体取值, 并且相邻两个取等的概率为 \(\frac{1}{\infty}\) , 即为 \(0\) .
考虑构造一个序列 \(b_i=[a_i<a_{i-1}]+a_i-a_{i-1}\) , 那么值域为 \(b_i\in[0,1)\) , 所以问题转化为 \(k-1\leqslant \sum{b_i}<k\) 的概率.
问题再次转化为在 \((0,0,\dots,0)\) 到 \((1,1,\dots,1)\) 的超立方体中等概率的取一个点, 记为 \((c_1,c_2,\dots,c_n)\) , 设 \(f_{k}\) 为满足这个点 \(\sum{c_i}<k\) 的概率, 此时的 \(c_i\) 仍小于 \(1\) , 答案则为 \((f_{k}-f_{k-1})n!\) .
而 \(f_{k}\) 则是超立方体被超平面 \(\theta:\sum{c_i}=k\) 切割后的体积与原体积之比 (原体积就是 \(1\) ) .
事实上概率的本质也是如此, 符合条件的样本与样本空间之比, 即一个超立方体被一个或多个超平面切割后的体积.
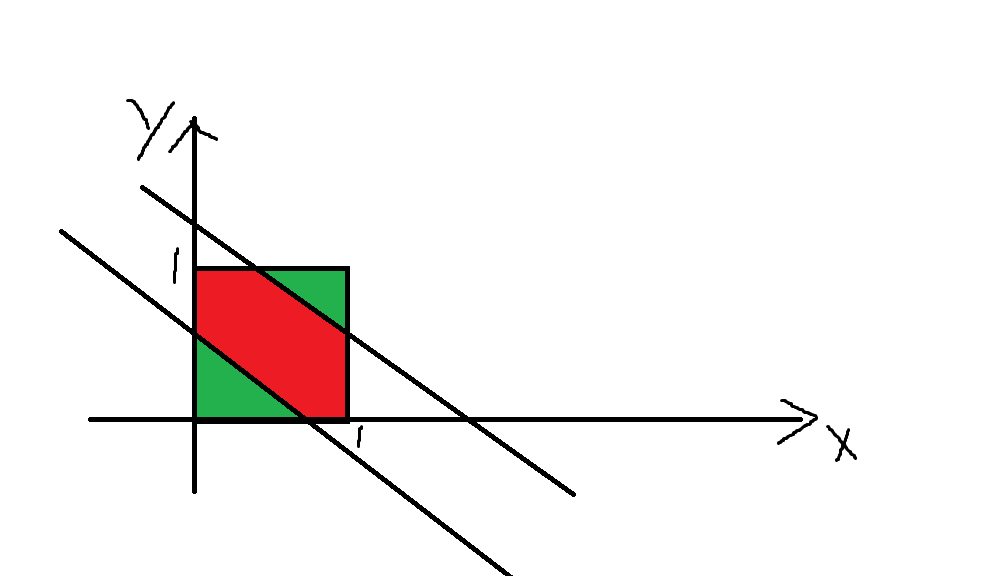
这里给出二维平面的演示, 在 \(x,y\in[0,1]\) 的情况下有 \(x+y\) 在某个区间上的概率.
红色即为符合要求的概率, 红色加绿色即为超立方体.
在此问题中, 超平面与坐标轴形成的体积即为 \(\frac{k^n}{n!}\) .
那符合条件的体积呢, 并不好算, 考虑容斥, 设 \(g_{x}\) 表示在超平面与坐标轴形成的 \(n\) 为图形中取一点, 点的坐标至少有 \(x\) 个维度大于等于 \(1\) (即不在超立方体上) 的概率.
这 \(x\) 维的取值在 \([1,k)\) 上, 钦定其减一变成 \([0,k-1)\) 对体积不造成影响 (这里不是指超立方体的体积, 而是超平面与坐标轴所构成的超立方体减去之前的超立方体所构成的体积) , 则总限制变成了 \(\sum{c_i}<k-x\) , 所以 \(g_{x}=\binom{n}{x}\frac{(k-x)^n}{n!}\) .
容斥之后即为 \(f_{k}=\sum\limits_{i=0}^{k-1}{(-1)^ig_i}\) . 时间复杂度 \(\mathcal{O}(n\log{n})\) .
标签:dots,概率,LOJ,sum,pjudge,体积,超平面,立方体,UOJ From: https://www.cnblogs.com/Lonely923/p/16758794.html