Description
给定一棵 \(n\) 个节点的树,每次询问编号为 \([l, r]\) 的点中有多少个是祖先关系。
\(n, q \le 10^5\)。
Solution
直接做的话树上的祖先关系不好统计,那么转化到 \(\texttt{dfs}\) 序上,如果 \(u\) 是 \(v\) 的祖先那么 \(dfn_u \le dfn_v < dfn_u + siz_u\)。
把 \([dfn_u, dfn_u + siz_u - 1]\) 看成一条线段,把树上的点拆成一条线段和一个点,那么问题就变成了用 \([l, r]\) 的线段覆盖 \([l, r]\) 的点,能够覆盖多少次。
首先对点分块,\(f_{i, j}\) 表示前 \(i\) 条线段在第 \(j\) 个块中能覆盖多少次,可以对每一个块中的点建一棵树状数组,加入一条线段就在对应的树状数组查询。
接下来考虑散点怎么处理,每次我们要处理一个散点在编号为 \([l, r]\) 的线段中被覆盖的次数,现在对于线段建主席树,把 \([l, r]\) 拆成主席树上的两个点,相减计算贡献。
那么在树状数组和主席树上要做 \(O(n \sqrt n)\) 次操作,时间复杂度 \(O(n \sqrt n \log n)\),把树状数组部分改成在树上 \(\texttt{dfs}\),然后调整块长可以做到 \(O(n \sqrt{n \log n})\),这是官方题解做法。
现在开始优化主席树部分,我们发现修改有只有 \(n\) 次,而查询有 \(n \sqrt n\) 次,使用主席树做修改是非常浪费的,考虑用可持久化值域分块平衡两部分复杂度。
分块本质上是一个树形结构,由于要可持久化,所以把分块树建出来,每一个块用一个关键点表示,每一个散点用一个叶子表示。
那么每次修改只会影响 \(O(\sqrt n)\) 个关键点,以及散块的 \(O(\sqrt n)\) 个叶子,对于散块我们暴力复制所有点重构一遍,所有代表整块的关键点我们也复制一份,但是只在这些点上打标记,不递归到它下面的叶子。
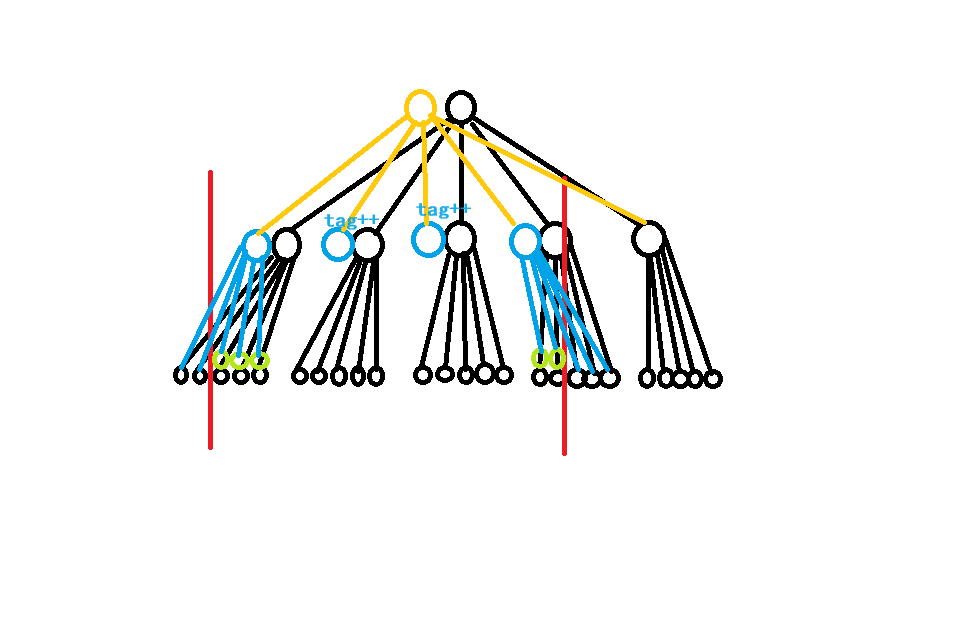
容易发现单词修改只会影响 \(O(\sqrt n)\) 个点,从而时空复杂度为 \(O(n \sqrt n)\)。
Code
这里放上卡常前的代码。
点击查看代码
#include <iostream>
#include <vector>
#pragma GCC optimize("Ofast")
using namespace std;
using LL = long long;
const int N = 1e5 + 5;
const int kL = 318, M = N / kL + 2;
const int tL = N * kL;
int n, q, now;
int fa[N], dfn[N], siz[N];
int rt[N * 2];
int bl[N], cnt;
int L[M], R[M], f[N][M];
vector<int> e[N];
void dfs (int u) {
dfn[u] = ++now;
siz[u] = 1;
for (auto v : e[u]) {
if (v != fa[u]) {
dfs(v);
siz[u] += siz[v];
}
}
}
struct tree {
int totr, tots, totl, toti;
int son[N * 3][kL + 2];
int lson[N * 4 + kL][kL + 2];
int val[tL * 2], tag[tL], id[tL];
void builds (int &k, int l, int r) {
k = ++tots, id[k] = ++toti;
for (int i = l; i <= r; ++i) {
lson[id[k]][i - l + 1] = ++totl;
}
}
void build (int &k) {
k = ++totr;
for (int i = 1; i <= cnt; ++i) {
builds(son[k][i], L[i], R[i]);
}
}
void adds (int t, int &k, int l, int r, int L, int R) {
id[k = ++tots] = ++toti, tag[k] = tag[t];
copy(lson[id[t]] + 1, lson[id[t]] + R - L + 2, lson[id[k]] + 1);
for (int i = l; i <= r; ++i) {
int p = ++totl;
val[p] = val[lson[id[t]][i - L + 1]] + 1;
lson[id[k]][i - L + 1] = p;
}
}
void addall (int t, int &k) {
id[k = ++tots] = id[t], tag[k] = tag[t] + 1;
}
void add (int t, int &k, int l, int r) {
k = ++totr;
int bl = ::bl[l], br = ::bl[r];
copy(son[t] + 1, son[t] + cnt + 1, son[k] + 1);
if (bl == br) {
adds(son[t][bl], son[k][bl], l, r, L[bl], R[bl]);
}
else {
adds(son[t][bl], son[k][bl], l, R[bl], L[bl], R[bl]);
adds(son[t][br], son[k][br], L[br], r, L[br], R[br]);
for (int i = bl + 1; i < br; ++i) {
addall(son[t][i], son[k][i]);
}
}
}
int count (int k, int x) {
int s = son[k][bl[x]];
return val[lson[id[s]][x - L[bl[x]] + 1]] + tag[s];
}
} t;
LL query (int x, int l, int r) {
int bl = ::bl[l], br = ::bl[r];
auto qry = [&](int i) -> int {
return t.count(rt[x], dfn[i]);
};
LL res = 0;
if (bl == br) {
for (int i = l; i <= r; ++i) {
res += qry(i);
}
}
else {
for (int i = l; i <= R[bl]; ++i) {
res += qry(i);
}
for (int i = bl + 1; i < br; ++i) {
res += f[x][i];
}
for (int i = L[br]; i <= r; ++i) {
res += qry(i);
}
}
return res;
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 2; i <= n; ++i) {
cin >> fa[i];
e[fa[i]].push_back(i);
}
dfs(1);
for (int i = 1; i <= n; ++i) {
bl[i] = (i - 1) / kL + 1;
}
cnt = bl[n];
for (int i = 1; i <= cnt; ++i) {
L[i] = R[i - 1] + 1;
R[i] = min(L[i] + kL - 1, n);
}
t.build(rt[0]);
for (int i = 1; i <= cnt; ++i) {
for (int j = L[i]; j <= R[i]; ++j) {
t.add(rt[(j != L[i]) * (j - 1 + n)], rt[j + n], dfn[j], n);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= cnt; ++j) {
f[i][j] = f[i - 1][j] + t.count(rt[R[j] + n], dfn[i] + siz[i] - 1) - t.count(rt[R[j] + n], dfn[i] - 1);
}
}
for (int i = 1; i <= n; ++i) {
t.add(rt[i - 1], rt[i], dfn[i], dfn[i] + siz[i] - 1);
}
cin >> q;
for (LL la = 0, l, r; q--; ) {
cin >> l >> r;
l ^= la, r ^= la;
l = l % n + 1, r = r % n + 1;
if (l > r) swap(l, r);
cout << (la = (query(r, l, r) - query(l - 1, l, r))) << '\n';
}
return 0;
}