算法题解——买卖股票的最佳时机

解题思路

先考虑最简单的「暴力遍历」，即枚举出所有情况，并从中选择最大利润。设数组 prices 的长度为n，由于只能先买入后卖出，因此第 1 天买可在未来n−1天卖出，第 2 天买可在未来n - 2天卖出……以此类推，共有

种情况，时间复杂度为O(N^2)。考虑到题目给定的长度范围 1≤prices.length≤10^5 ，需要思考更优解法。

然而，暴力法会产生许多冗余计算。例如，若第 1 天价格低于第 2 天价格，即第 1 天成本更低，那么我们一定不会选择在第 2 天买入。进一步的，若在前i天选择买入，若想达到最高利润，则一定选择价格最低的交易日买入。考虑根据此贪心思想，遍历价格列表 prices 并执行两步：

由于初始值i=0，为了序号对应，本文设从第 0 天开始；

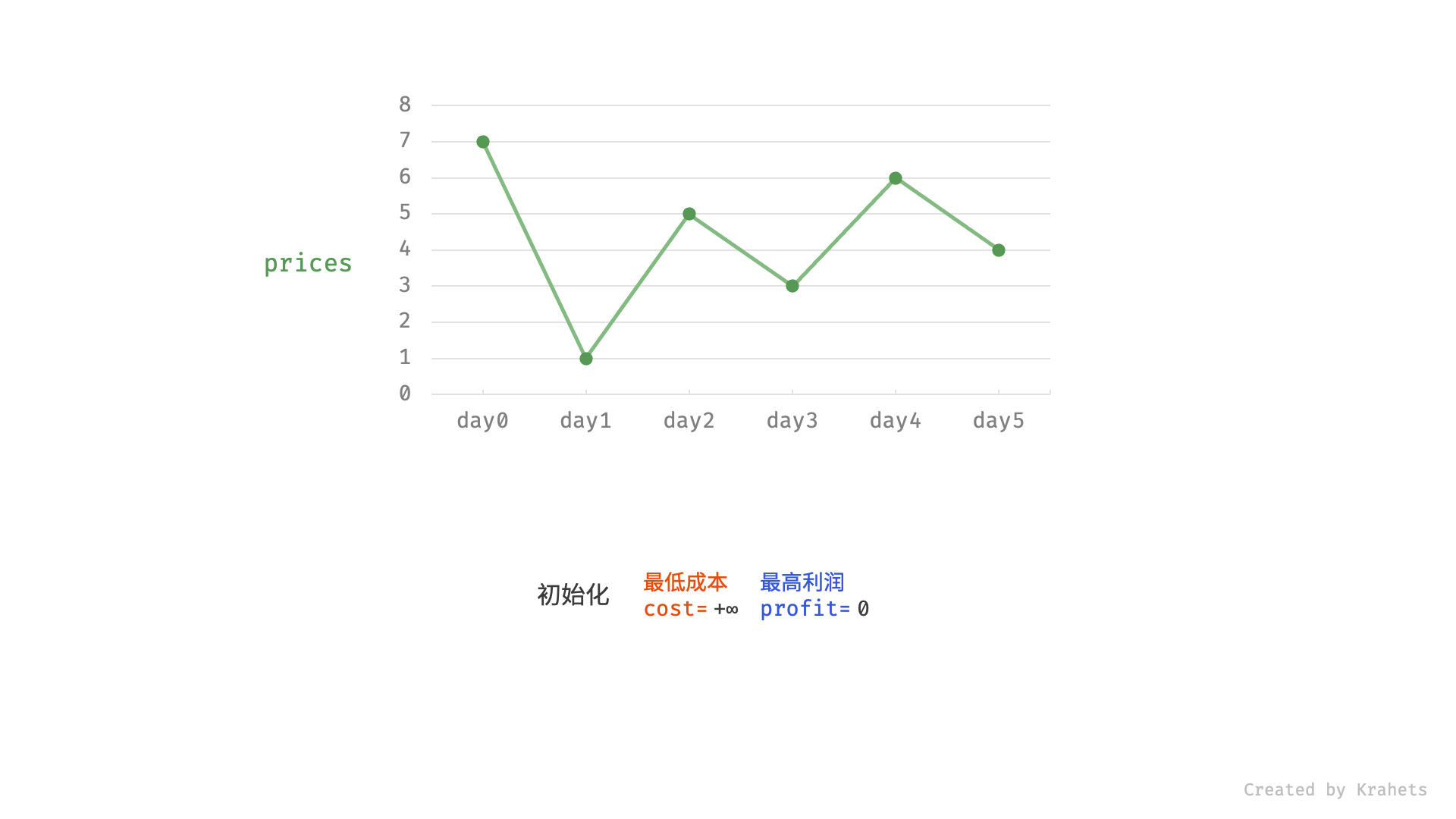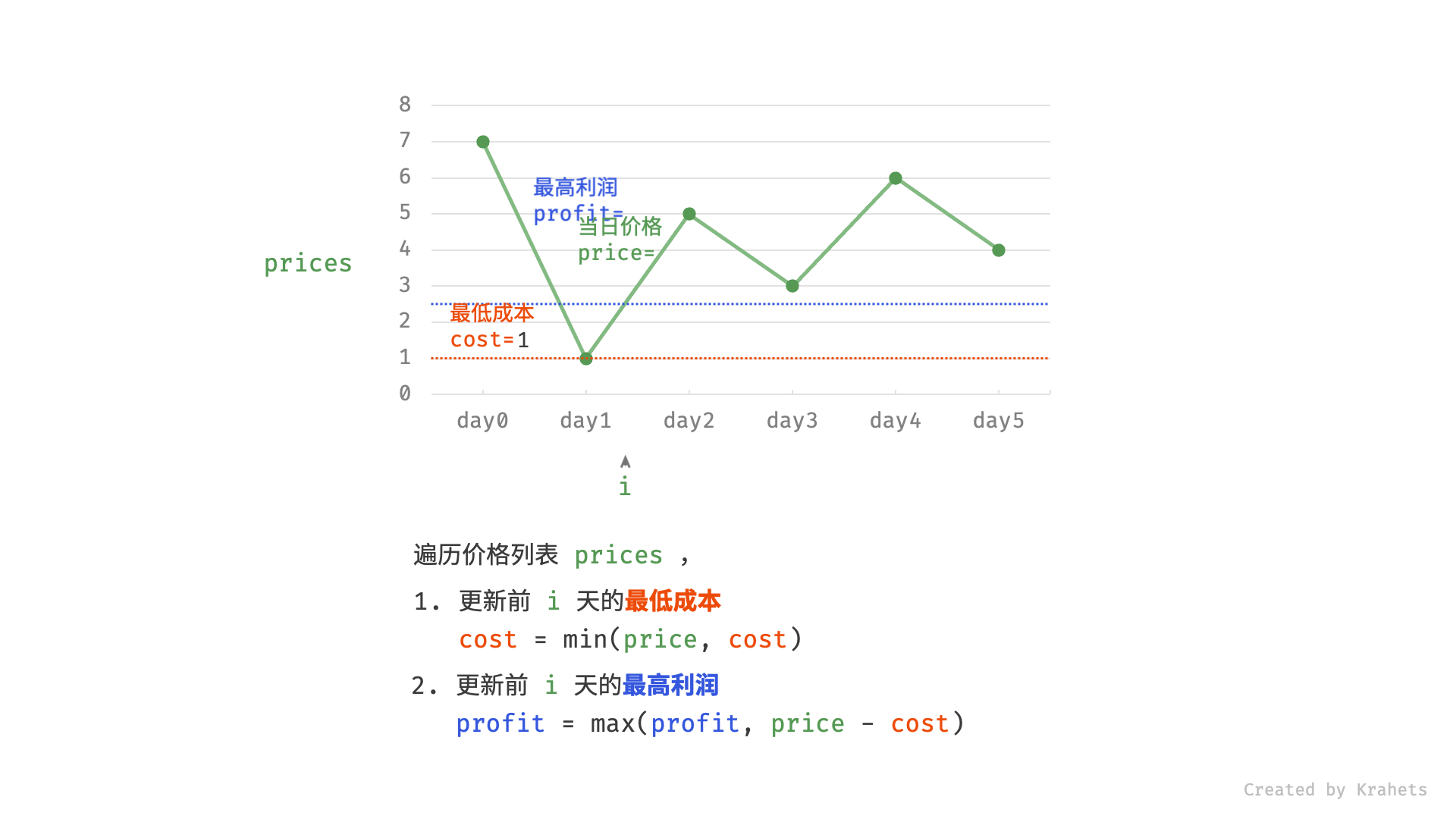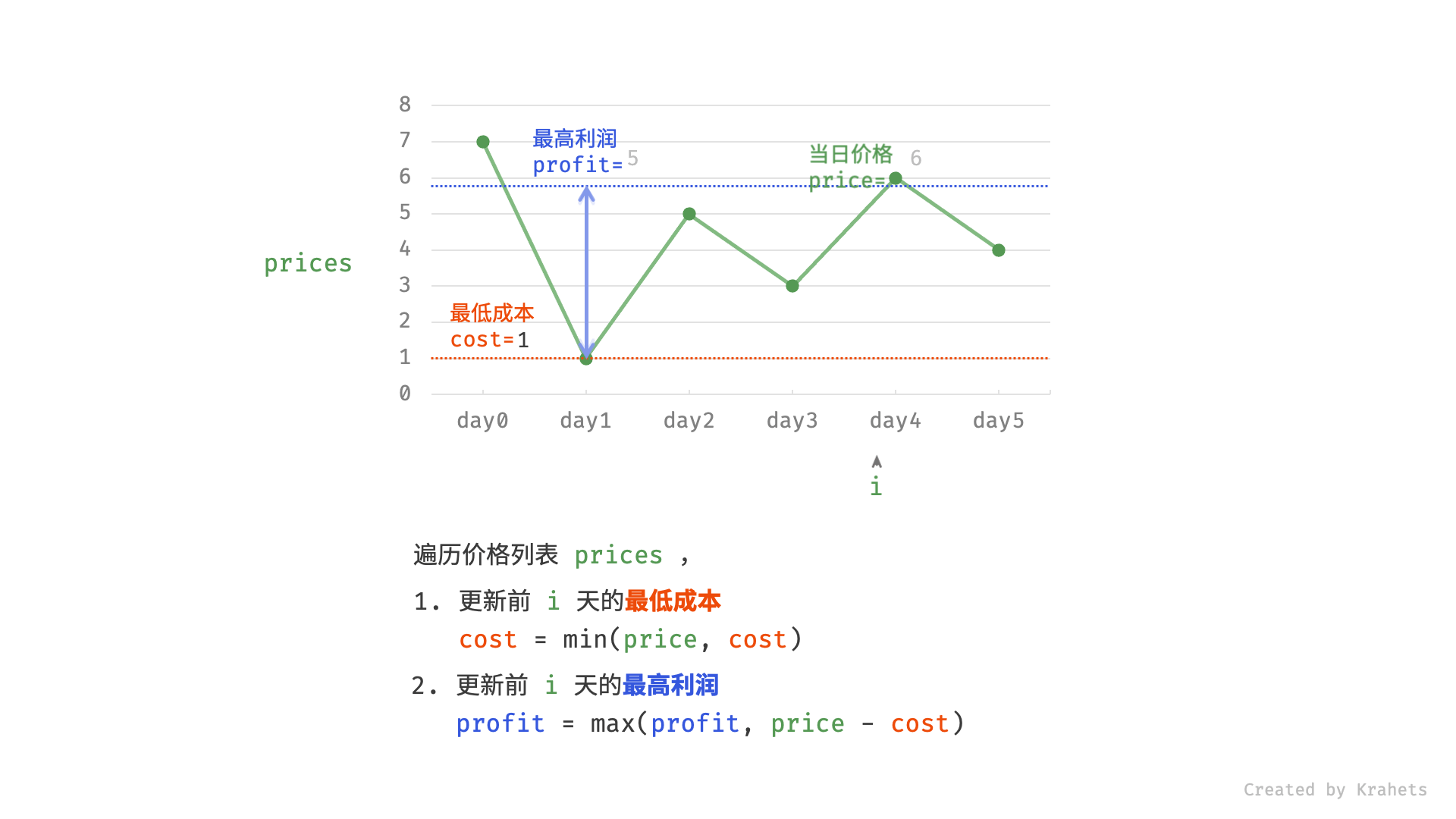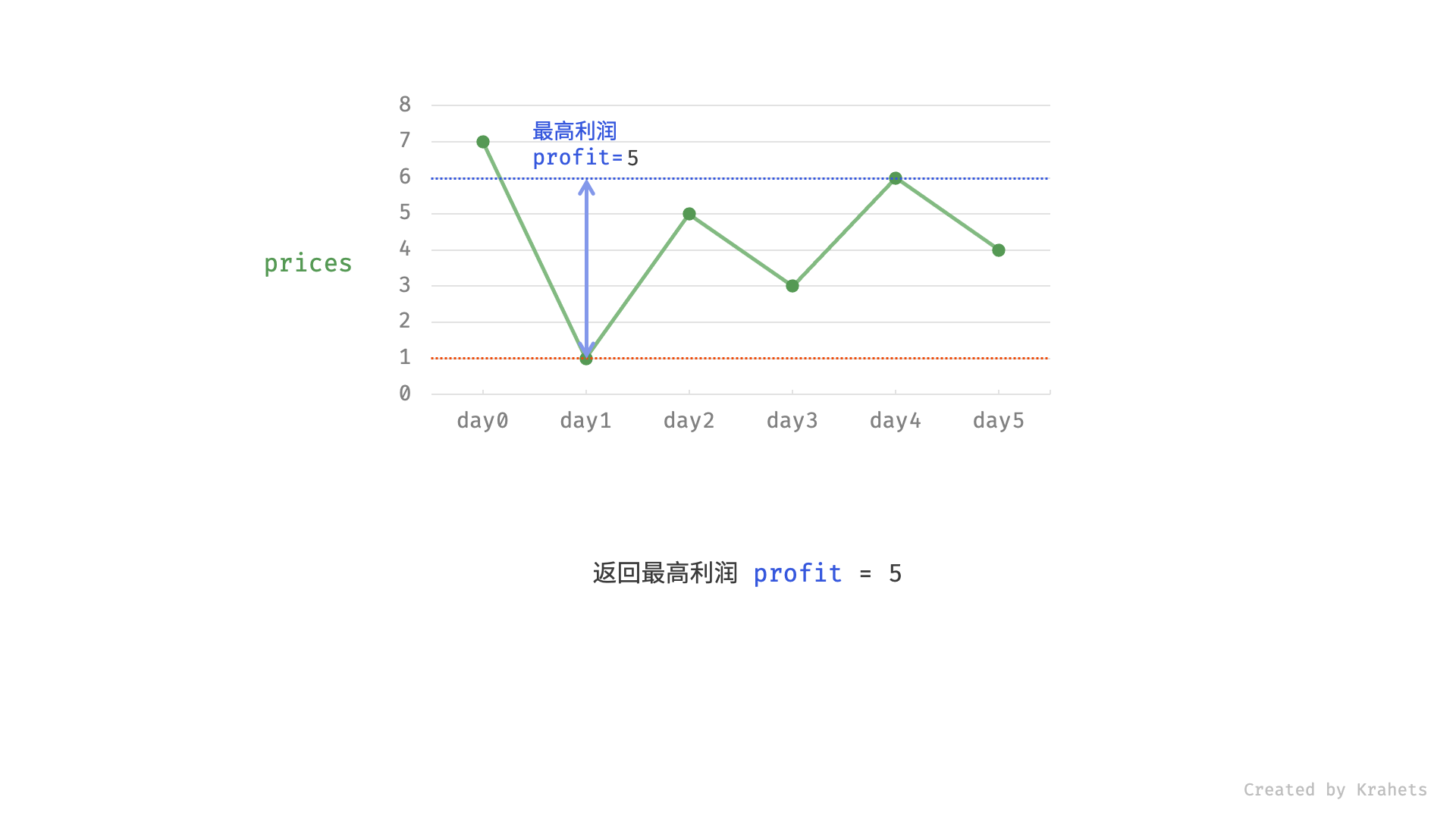
1. 更新前i天的最低价格，即最低买入成本 cost；
2. 更新前i天的最高利润 profit ，即选择「前i-1天最高利润 profit 」和「第i天卖出的最高利润 price - cost 」中的最大值 ；

代码

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE, profit = 0;
        for (int price : prices) {
            cost = Math.min(cost, price);
            profit = Math.max(profit, price - cost);
        }
        return profit;
    }
}

复杂度分析

• 时间复杂度为O(N)：其中N为数组 prices 长度。遍历 prices 使用线性时间。
• 空间复杂度 为O(1)：变量 cost , profit 使用 O(1)空间。
  
  
  

参考资料：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/solutions/1692872/by-jyd-cu90/?envType=study-plan-v2&envId=top-interview-150