题解：CF118E

Tarjan

思路

先来看一下题目给出的无解的这个样例。

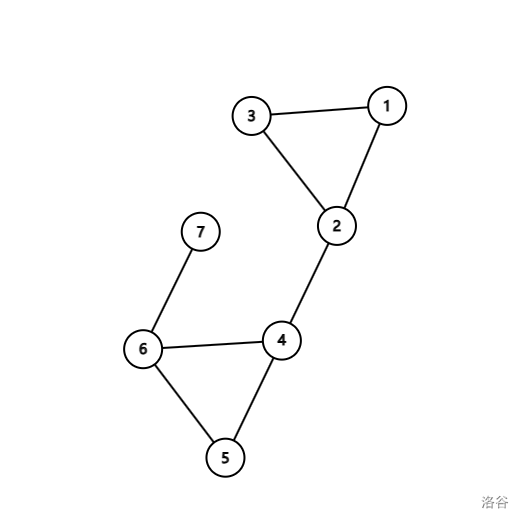
不难发现，导致无解的两条边就是 \(6 - 7\) 和 \(2 - 4\) 这两个桥。所以这个题就转换成了求桥，如果存在桥就是无解。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=3e5+5;
inline int read();
int n,m,cnt=1,head[N],idx,dfn[N],low[N],anscnt;
bool flag,vis[M<<1];
struct E{
	int to,nex,u;
}edge[M<<1];
struct A{
	int x,y;
}ans[M<<1];
void add(int u,int v)
{
	edge[++cnt].to=v;
	edge[cnt].u=u;
	edge[cnt].nex=head[u];
	head[u]=cnt;
}
void tarjan(int x,int fa)
{
	dfn[x]=low[x]=++idx;
	for(int i=head[x];i;i=edge[i].nex)
	{
		int to=edge[i].to;
		if(!dfn[to])
		{
			tarjan(to,x);
			low[x]=min(low[to],low[x]);
			ans[++anscnt]=(A({x,to}));
			if(low[to]>dfn[x])
			{
				flag=1;
				return ;
			}
		}
		else if(to!=fa&&dfn[to]<dfn[x])
		{
			low[x]=min(low[x],dfn[to]);
			ans[++anscnt]=(A({x,to}));//记录一下答案
		}
	}
}
int main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		int x,y;
		x=read();y=read();
		ans[i].x=x;ans[i].y=y;
		add(x,y);
		add(y,x);
	}
	tarjan(1,0);
	if(flag)
	{
		puts("0");
		return 0;
	}
	for(int i=1;i<=anscnt;i++)
	{
		printf("%d %d\n",ans[i].x,ans[i].y);
	}
	return 0;
}

inline int read()
{
	int x=0,f=1;
	char ch;
	ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-') f=-f;ch=getchar();}
	while(ch<='9'&&ch>='0')
	{
		x=(x<<1)+(x<<3)+(ch&15);
		ch=getchar();
	}
    return x*f;
}