前言
莫队可以解决许多其他数据结构无法完成的问题,正在很多其他问题上也可以拿部分分甚至满分,只因其复杂度为小常数 \(O(n\sqrt n \times k)\)
其中 \(k\) 是单次扩张以及收缩的复杂度,而二离莫队可以在答案可差分的情况下达到 \(O(n\sqrt n + n \times k)\)
起源
lxl把二次离线莫队这个科技在洛谷的一场月赛里首次亮相
\(-->\)
例题 P4887 【模板】莫队二次离线(第十四分块(前体))
珂朵莉给了你一个序列 \(a\),每次查询给一个区间 \([l,r]\),查询 \(l \leq i< j \leq r\),且 \(a_i \oplus a_j\) 的二进制表示下有 \(k\) 个 \(1\) 的二元组 \((i,j)\) 的个数。\(\oplus\) 是指按位异或。
对于100%的数据,\(1 \leq n, m \leq 100000\),\(0 \leq a_i, k < 16384\)。
思路
首先 \(k>14\) 肯定无解
考虑 \(k \leq 14\) 的情况
因为值域 \(V\) 很小,所以可以把二进制下有 \(k\) 个 \(1\) 数用桶装起来
而 \(a \bigotimes b = c\) 时有 \(a \bigotimes c = b\)
然后加入一个数 \(x\) 时直接把所有桶里的数与 \(x\) 的异或值出现次数 \(+1\)
但是暴力加的话复杂度会到 \(n \sqrt n \times C_{14}^{k}\)
考虑使用二离优化
设当前莫队指针为 \(l\) , \(r\)
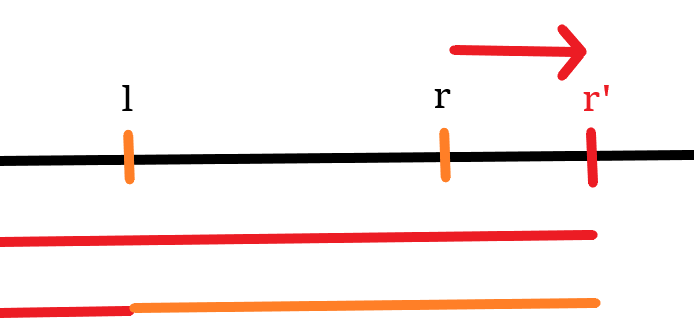
\(r\) 要移动到 \(r'\) ,则答案变化量为 \([r+1,r']\) 对 \([l,r']\) 的贡献
差分转化成 \([r+1,r']\) 对 \([1,r']\) 减去 \([r+1,r']\) 对 \([1,l-1]\)
第一部分可以转化成区间 \([1,r']\) 的答案减去 \([1,r]\) 的答案
提前预处理 \([1,i]\) 区间的答案即可
第二部分我们离线扫描 \(l\) 即可
再看移动 \(l\)
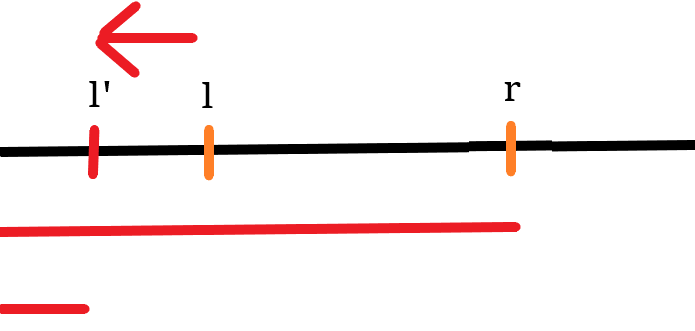
考虑 \(l\) 移动到 \(l'\)
变化量是 \([l',l-1]\) 对 \([l',r]\) 的贡献
拆分成 \([l',l-1]\) 对 \([1,r]\) 的贡献减去 \([l',l-1]\) 对 \([1,l'-1]\) 的贡献
第二部分可以转化成 \([1,l]\) 答案减 \([1,l'-1]\) 的答案
另外的一起扫描即可
代码:
#include<bits/stdc++.h>
#define ll long long
#define SF scanf
#define PF printf
#define PB push_back
#define ull unsigned long long
#define R register
#define rep(i,x,y) for(R int i=x;i<=y;i++)
using namespace std;
int n,m,k,sq,a[100010],pos[100010];
ll sum[100010],ans[100010],t[20010],f[100010];
vector<int> d;
int Get(int x){
int ret=0;
for(;x>0;x-=(x&-x)) ret++;
return ret;
}
struct node{
int l,r,id;
}p[100010];
inline bool cmp(node x,node y){
if(pos[x.l]!=pos[y.l]) return x.l<y.l;
if(pos[x.l]&1) return x.r<y.r;
return x.r>y.r;
}
struct qry{
int l,r,p,i;
friend bool operator <(qry x,qry y){
return x.p<y.p;
}
}q[200010];
int main(){
SF("%d%d%d",&n,&m,&k);
sq=sqrt(n);
if(k>14){
rep(i,1,m) puts("0");
return 0;
}
rep(i,1,n) SF("%d",&a[i]),pos[i]=(i-1)/sq+1;
rep(i,0,16383) if(Get(i)==k) d.PB(i);
rep(i,1,m) SF("%d%d",&p[i].l,&p[i].r),p[i].id=i;
rep(i,1,n){
f[i]=t[a[i]]; f[i]+=f[i-1];
for(int j:d) ++t[j^a[i]];
}
sort(p+1,p+1+m,cmp);
int l=1,r=0,s=0;
rep(i,1,m){
if(l<p[i].l) q[++s]={l,p[i].l-1,r,-i},sum[i]+=f[p[i].l-1]-f[l-1],l=p[i].l;
if(r<p[i].r) q[++s]={r+1,p[i].r,l-1,-i},sum[i]+=f[p[i].r]-f[r],r=p[i].r;
if(r>p[i].r) q[++s]={p[i].r+1,r,l-1,i},sum[i]-=f[r]-f[p[i].r],r=p[i].r;
if(l>p[i].l) q[++s]={p[i].l,l-1,r,i},sum[i]-=f[l-1]-f[p[i].l-1],l=p[i].l;
}
sort(q+1,q+1+s);
int np=0;
rep(i,0,16383) t[i]=0;
rep(i,1,s){
while(np<q[i].p){
++np;
for(int j:d) ++t[j^a[np]];
}
rep(j,q[i].l,q[i].r) q[i].i>0?sum[q[i].i]+=(t[a[j]]-(j<=np&&!k)):sum[-q[i].i]-=(t[a[j]]-(j<=np&&!k));
}
rep(i,1,m) sum[i]+=sum[i-1],ans[p[i].id]=sum[i];
rep(i,1,m) PF("%lld\n",ans[i]);
return 0;
}
练习 P5398 [Ynoi2018] GOSICK
题意:
维多利加给了你一个序列 \(a\),每次询问给一个区间 \([l,r]\)。
查询 \(l \leq i,j\leq r\),且 \(a_i\) 是 \(a_j\) 倍数的二元组 \((i,j)\) 的个数。
记录一个 \(cnt\) 数组,其中 \(cnt[i]\) 代表 \(i\) 的倍数个数
不过单次修改时,一个数因数个数是 \(\sqrt V\) 的
先根号分治,前缀和 \(\leq \sqrt V\) 数的倍数个数
大于 \(\sqrt V\) 的跑二离莫队即可
时间复杂度 \(O(n \sqrt n +n\sqrt V)\)
具体细节看代码吧
#include<stdio.h>
#include<algorithm>
#include<vector>
#include<math.h>
#include<iostream>
#define ll long long
#define PB push_back
#define ull unsigned long long
#define R register
#define rep(i,x,y) for(R int i=x;i<=y;i++)
using namespace std;
const int MAXN=500000,V=500000,W=120;
int n,m,sq,a[MAXN+10],num1[MAXN+10],num2[MAXN+10],bl[MAXN+10],cnt[V+10],cnt1[V+10],cnt2[V+10];
ll f[MAXN+10],sum[MAXN+10],ans[MAXN+10];
vector<int> F[V+10];
inline int read(){
int x=0;
char ch=getchar();
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch-'0'),ch=getchar();
return x;
}
struct node{
int l,r,id;
}q[MAXN+10];
inline bool tmp1(node x,node y){
if(bl[x.l]!=bl[y.l]) return x.l<y.l;
if(bl[x.l]&1) return x.r<y.r;
return x.r>y.r;
}
struct qry{
int l,r,p,id;
}Q[MAXN*2+10];
inline bool tmp2(qry x,qry y){
return x.p<y.p;
}
int main(){
// freopen("P5398.in","r",stdin);
// freopen("P5398_1.out","w",stdout);
n=read(),m=read(); sq=m/sqrt(n);
rep(i,1,n) a[i]=read(),bl[i]=(i-1)/sq+1;
rep(i,1,m) q[i]={read(),read(),i};
sort(q+1,q+1+m,tmp1);
rep(i,1,n){
if(!F[a[i]].size()){
for(R int j=1;j*j<=a[i];j++){
if(a[i]%j==0){
num1[j]++;
f[i]+=cnt[j]; F[a[i]].PB(j);
if(j*j!=a[i]) num1[a[i]/j]++,f[i]+=cnt[a[i]/j];
}
}
}else{
for(R int j:F[a[i]]){
num1[j]++;
f[i]+=cnt[j];
if(j*j!=a[i]) num1[a[i]/j]++,f[i]+=cnt[a[i]/j];
}
}
f[i]+=f[i-1]+num1[a[i]];
// cout<<f[i]<<'\n';
cnt[a[i]]++;
}
int l=1,r=0,s=0;
rep(i,1,m){
if(r<q[i].r){
Q[++s]={r+1,q[i].r,l-1,-i};
sum[i]+=f[q[i].r]-f[r];
r=q[i].r;
}
if(r>q[i].r){
Q[++s]={q[i].r+1,r,l-1,i};
sum[i]-=f[r]-f[q[i].r];
r=q[i].r;
}
if(l>q[i].l){
Q[++s]={q[i].l,l-1,r,i};
sum[i]-=f[l-1]-f[q[i].l-1];
l=q[i].l;
}
if(l<q[i].l){
Q[++s]={l,q[i].l-1,r,-i};
sum[i]+=f[q[i].l-1]-f[l-1];
l=q[i].l;
}
// sum[i]+=q[i].r-q[i].l+1;
}
int nowp=0;
sort(Q+1,Q+1+s,tmp2);
rep(i,1,s){
while(nowp<Q[i].p){
++nowp;
for(R int j:F[a[nowp]]) num2[j]++,num2[a[nowp]/j]+=(j*j!=a[nowp]);
if(a[nowp]>W) for(R int j=1;j*a[nowp]<=V;j++) num2[j*a[nowp]]++;
}
rep(j,Q[i].l,Q[i].r) Q[i].id<0?sum[-Q[i].id]-=num2[a[j]]:sum[Q[i].id]+=num2[a[j]];
}
// rep(i,1,m) cout<<l<<' '<<r<<' '<<sum[i]<<endl;
rep(i,1,W){
rep(j,1,n){
cnt1[j]=cnt1[j-1]+(a[j]==i);
cnt2[j]=cnt2[j-1]+(a[j]%i==0);
}
rep(j,1,s){
ll w=1ll*cnt1[Q[j].p]*(cnt2[Q[j].r]-cnt2[Q[j].l-1]);
Q[j].id<0?sum[-Q[j].id]-=w:sum[Q[j].id]+=w;
}
}
rep(i,1,m) sum[i]+=sum[i-1],ans[q[i].id]=sum[i];
rep(i,1,m) printf("%lld",ans[i]),putchar('\n');
return 0;
}
常数?挺小的
\[\large End \] 标签:int,rep,离线,笔记,leq,long,莫队,define From: https://www.cnblogs.com/yzq-yzq/p/17759827.html