平衡树真的恶心死了!!!!!!好烦啊,又臭又长。
有很多种平衡树,替罪羊, treap,fhq, slpay。这里就说 splay, 和 bst 和 替罪羊 了,因为其他我都不会(悲
先说二叉排序树(二叉搜索树), 他的关系就是 左子树所有节点 < 根节点 < 右子树所有节点。也就是说,按照中序遍历可以找到有序序列。

这个时候我们就可以增删改(删了再加入)查了!
查找 通过搜索,发现如果这个节点等于自己,cnt++, 小于自己往左搜索,大于自己往右边搜索
比如说我们要增加,搜索,如果发现没有,就新增节点。
删除, 找到位置(同上)cnt--。
这个时候就发现一个很严重的问题,它的复杂度是树高,就有可能变成一条链,复杂度瞬间变成 \(O(n)\) (泰裤辣)。
平衡树要来了!
平衡树还有几个功能
- 要求排名
- 按照排名查数
- 前驱后继
替罪羊的思路就此诞生。 如果发现不平衡,就重构。
平衡的定义是非0节点占全部的 M% 以内,且左节点的个数在 右节点的 M% 一内。
发现不平衡后就把它变成线性的,再按照贪心思路,每次折半重构。
M 在 70 ~ 75 为最佳
代码就不贴了,因为很丑。
接下来就是 splay 了
splay的主要思路就是操作的数都要旋转到树顶端
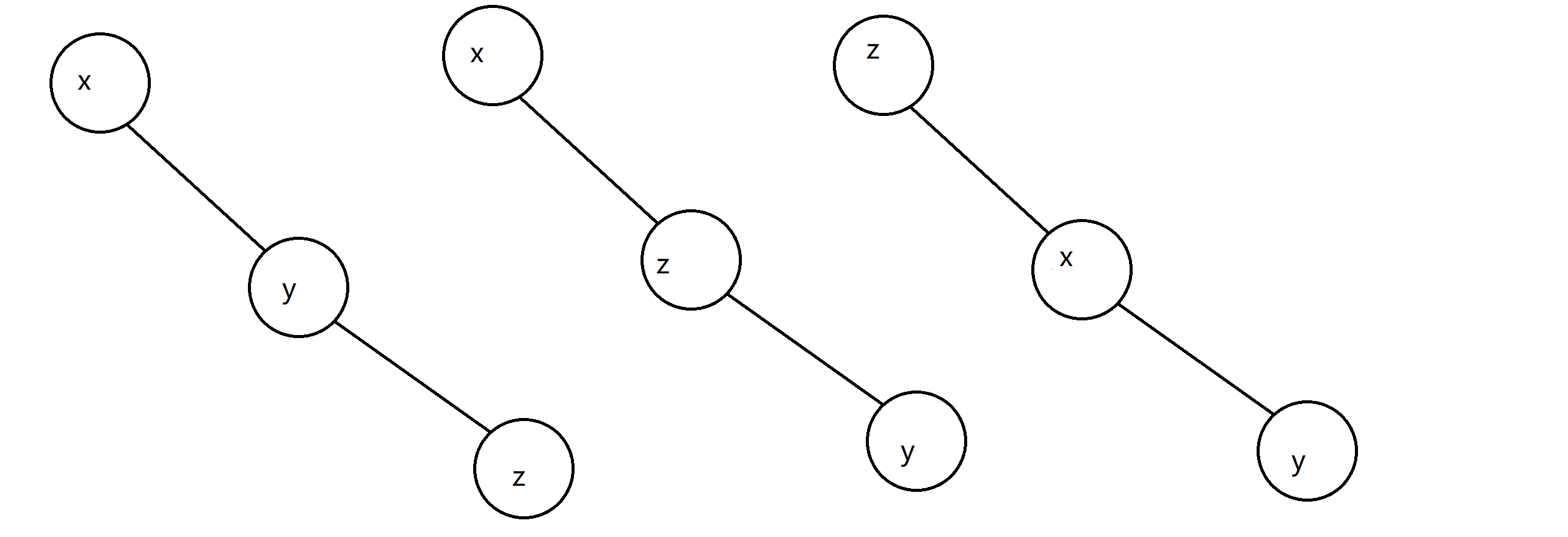
这个时候就要提到左旋和右旋了。其实就是传统的左旋和右旋,还是讲一下吧。

如图是左旋,右旋就是反过来,将x往上面旋,只需要看x是左儿子,还是右儿子就可以了。
然而,无脑的旋转会被善良的出题人卡掉。
所以,我们就要牵扯到祖宗——爸爸的爸爸叫什么(
两种情况,第一种,如下图
先旋转自己,再旋转自己。
第二种,如下图
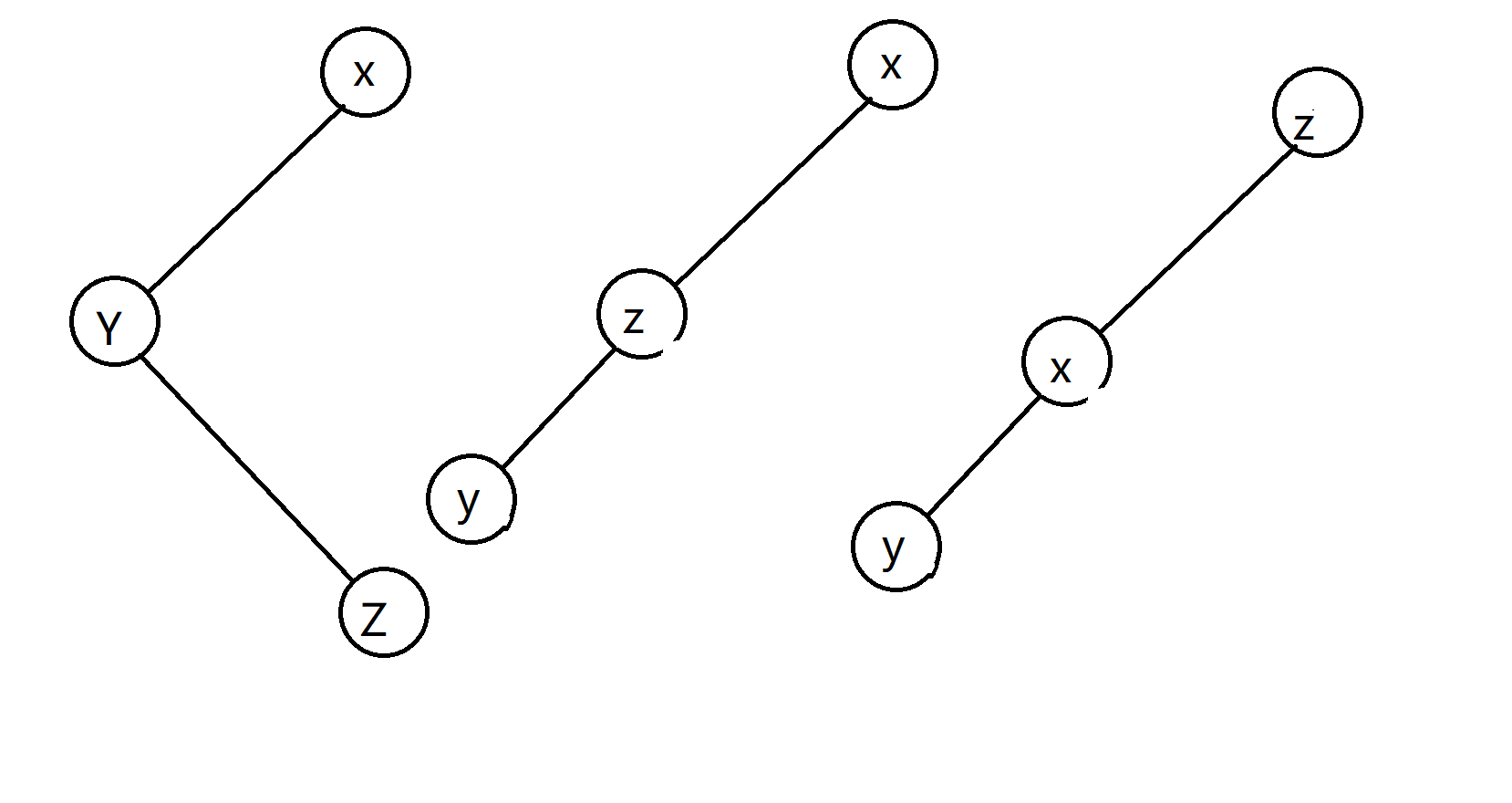
先转父亲,再转自己。
然后就是紧张刺激的写代码环节了!
bool check(int x) {
return a[a[x].fa].ch[0] != x;
}
写一个函数判断是做儿子(0)还是右儿子(1)。
void push_up(int rt) {
a[rt].size = a[a[rt].ch[0]].size + a[a[rt].ch[1]].size + a[rt].cnt;
}
更新自己,记得加上自己的个数。
void Add(int x, int y, bool f) {
a[y].ch[f] = x;
a[x].fa = y;
}
x接在y的(f ? "右儿子" : "左儿子")上。
正片,开始。
如果x是左儿子,就左旋,否则就是右旋,这样就可以简单轻松的完成自动的完成旋转了(dig, zig害人啊)
void rotate(int x) {
int y = a[x].fa, z = a[y].fa, d = check(x), w = a[x].ch[d ^ 1];
Add(w, y, d);
Add(x, z, check(y));
Add(y, x, d ^ 1);
push_up(y), push_up(x);
}
单次旋转函数,将x向上旋转。
void splay(int x, int p = 0) {
for (int f = a[x].fa; f = a[x].fa, f != p; rotate(x)) {
if (a[f].fa != p) {
if (check(f) == check(x)) {
rotate(f);
} else {
rotate(x);
}
}
}
if (p == 0) Rt = x;
}
多次旋转函数,将 x 旋顶。
void find(int x) {
int p = Rt;
while (a[p].ch[x > a[p].v] && x != a[p].v) {
p = a[p].ch[x > a[p].v];
}
splay(p);
}
查找并旋转到顶。
void insert(int x) {
int p = Rt, fa = 0;
while (p && x != a[p].v) {
fa = p;
p = a[p].ch[x > a[p].v];
}
if (p)
a[p].cnt++;
else {
p = ++cnt;
if (fa) a[fa].ch[x > a[fa].v] = p;
a[p] = MakeSplay(x, fa);
}
splay(p);
}
找到,如果已经有了就cnt++,否则添加。
int pre_suc(int x, int f) {
find(x);
if (!f && a[Rt].v < x || f && a[Rt].v > x) return Rt;
int p = a[Rt].ch[f];
while (a[p].ch[f ^ 1]) {
p = a[p].ch[f ^ 1];
}
return p;
}
前驱0, 后驱1。先旋转到顶,然后查找。
注意了,删除不一样
void remove(int x) {
int last = pre_suc(x, 0), next = pre_suc(x, 1);
splay(last), splay(next, last);
int p = a[next].ch[0];
if (a[p].cnt > 1) {
a[p].cnt--;
splay(p);
} else {
a[next].ch[0] = 0;
push_up(next), push_up(last);
}
}
先把x的前驱旋转到顶,再将后继旋到前驱的后面。那么后继的左儿子就是 x,而且 x 没有儿子。
int rank1(int x) {
int p = Rt;
while (1) {
if (a[p].ch[0] && a[a[p].ch[0]].size >= x) {
p = a[p].ch[0];
} else if (x > a[a[p].ch[0]].size + a[p].cnt) {
x -= a[a[p].ch[0]].size + a[p].cnt;
p = a[p].ch[1];
} else {
return p;
}
}
}
查排名为x的数,不多解释。
总代码来咯。
等等等等,还要加入最大值和最小值哦,不然有可能会没有前驱和后继哦(亲身
#include <iostream>
using namespace std;
const int kMaxN = 1e5 + 5;
int Rt, cnt;
struct Splay {
int v, fa, cnt, size, ch[2];
} a[kMaxN];
Splay MakeSplay(int v, int fa) {
Splay P;
P.v = v, P.fa = fa, P.cnt = P.size = 1, P.ch[0] = P.ch[1] = 0;
return P;
}
bool check(int x) {
return a[a[x].fa].ch[0] != x;
}
void push_up(int rt) {
a[rt].size = a[a[rt].ch[0]].size + a[a[rt].ch[1]].size + a[rt].cnt;
}
void Add(int x, int y, bool f) {
a[y].ch[f] = x;
a[x].fa = y;
}
void rotate(int x) {
int y = a[x].fa, z = a[y].fa, d = check(x), w = a[x].ch[d ^ 1];
Add(w, y, d);
Add(x, z, check(y));
Add(y, x, d ^ 1);
push_up(y), push_up(x);
}
void splay(int x, int p = 0) {
for (int f = a[x].fa; f = a[x].fa, f != p; rotate(x)) {
if (a[f].fa != p) {
if (check(f) == check(x)) {
rotate(f);
} else {
rotate(x);
}
}
}
if (p == 0) Rt = x;
}
void find(int x) {
int p = Rt;
while (a[p].ch[x > a[p].v] && x != a[p].v) {
p = a[p].ch[x > a[p].v];
}
splay(p);
}
void insert(int x) {
int p = Rt, fa = 0;
while (p && x != a[p].v) {
fa = p;
p = a[p].ch[x > a[p].v];
}
if (p)
a[p].cnt++;
else {
p = ++cnt;
if (fa) a[fa].ch[x > a[fa].v] = p;
a[p] = MakeSplay(x, fa);
}
splay(p);
}
int pre_suc(int x, int f) {
find(x);
if (!f && a[Rt].v < x || f && a[Rt].v > x) return Rt;
int p = a[Rt].ch[f];
while (a[p].ch[f ^ 1]) {
p = a[p].ch[f ^ 1];
}
return p;
}
void remove(int x) {
int last = pre_suc(x, 0), next = pre_suc(x, 1);
splay(last), splay(next, last);
int p = a[next].ch[0];
if (a[p].cnt > 1) {
a[p].cnt--;
splay(p);
} else {
a[next].ch[0] = 0;
push_up(next), push_up(last);
}
}
int rank1(int x) {
int p = Rt;
while (1) {
if (a[p].ch[0] && a[a[p].ch[0]].size >= x) {
p = a[p].ch[0];
} else if (x > a[a[p].ch[0]].size + a[p].cnt) {
x -= a[a[p].ch[0]].size + a[p].cnt;
p = a[p].ch[1];
} else {
return p;
}
}
}
int main() {
insert(0x3f3f3f3f);
insert(-0x3f3f3f3f);
int n, op, x;
for (cin >> n; n; n--) {
cin >> op >> x;
switch (op) {
case 1:
insert(x);
break;
case 2:
remove(x);
break;
case 3:
find(x), cout << a[a[Rt].ch[0]].size << '\n';
break;
case 4:
cout << a[rank1(x + 1)].v << '\n';
break;
case 5:
cout << a[pre_suc(x, 0)].v << '\n';
break;
case 6:
cout << a[pre_suc(x, 1)].v << '\n';
break;
}
}
return 0;
}