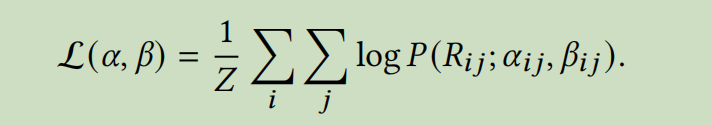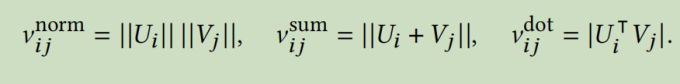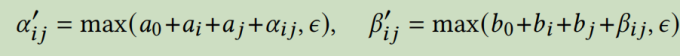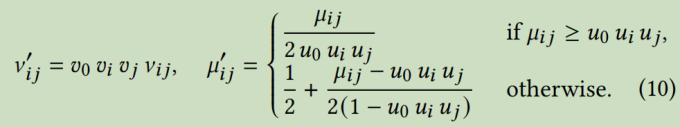A Lightweight Method for Modeling Confidence in Recommendations with Learned Beta Distributions论文阅读笔记

摘要

​ 大多数推荐系统并不提供对其决策信心的指示。因此，他们不区分确定的建议和不确定的建议。现有的RecSys置信方法要么是不准确的启发式，要么是在概念上复杂，因此现实世界的RecSys应用程序很少采用这些方法因为对他们的行为没有自信的见解

​ 在这项工作中，我们提出习得性beta分布作为一种简单和实用的推荐方法，具有明确的可信度测度。主要的观点是，beta分布作为概率分布来预测用户的偏好，它可以自然的在一个封闭区间上建模置信度，并且以最小的模型复杂性来实现。我们的结果表明，LBD保持了与现有方法有竞争力的准确性，同时在其准确性和置信度之间也有显著更强的相关性。此外，LBD在应用于高精度的目标推荐任务时具有更高的性能。

​ 我们的工作表明，在不牺牲简单性或准确性的情况下，建立推荐系统的可信度是可能的，也不引入沉重的计算复杂度。因此，我们希望它能更好地了解现实世界的系统，并为未来的新应用打开大门。

介绍

​ 用户偏好的建模仍然是一个非常困难的任务。部分原因是由于用户偏好中固有的不确定性：人类的行为是复杂的和随机的，不可能有完美的准确性预测。但是最常用的推荐系统模型在其预测中没有给出任何不确定性。也就是模型不能区分高度确定的预测和低不确定性的预测。因此目前的推荐系统没有什么时候提出可信的或者是怀疑的猜测的见解。

​ 一个好的可信度度量可以洞察系统的行为，并给出特定预测的误差程度。不确定性建模可以使推荐系统更可解释并对用户偏好进行更深入的研究。

​ 之前的工作通过应用生成概率模型来提出推荐系统。所有的现有工作都假设用户评级是来自高斯分布的样本。但是它们的计算很复杂。然后介绍了一些前人的改进工作以及缺点。提出目前的推荐系统领域似乎没有一种方法可以以一种优雅和可解释的方式有效的建模不确定性同时也要兼顾实际的计算要求

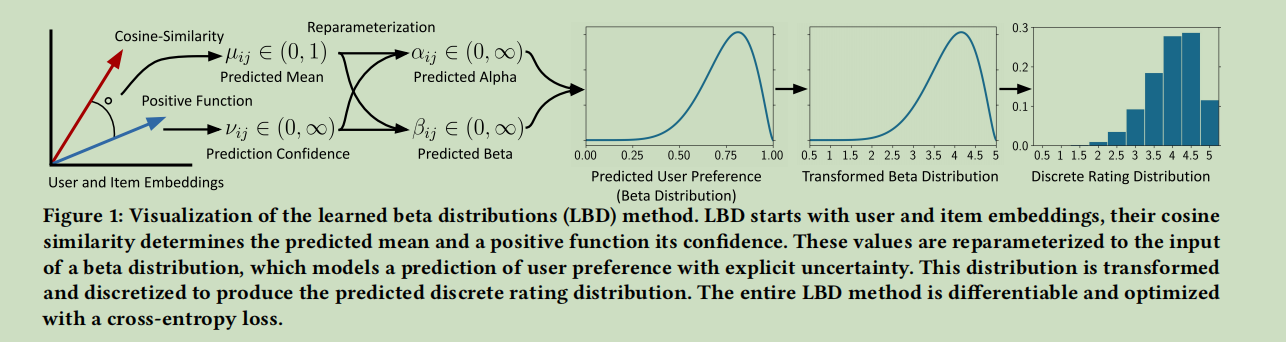
​ 在这项工作中，我们引入learned beta分布作为一种简单和轻量的推荐系统方法，用于一个自然的和显式的置信度模型度量。我们的方法将一个标准的beta分布转换为一个离散的评级分布。LBD可以在不同的用户-项目组合上改变它们的置信度，具有足够的模型表达性来捕获不确定性中的复杂模式。

​ 通过在RecSys中引入LBD，我们证明了在RecSys中的置信度建模是可能的，而不牺牲精度或增加计算复杂度。LBD的方法也很容易适用或扩展到更复杂的RecSys模型。

方法

​ 首先介绍了如何将beta分布转化为离散评级上的可优化分布。

​ 其次，提出了几种方法来建模每个用户-项目组合的唯一评级分布的参数

​ 第三，介绍了将用户偏差和项目偏差建模为模型参数的两种替代方案

​ 第四，提出了离散化的静态和自适应装箱策略

​ 第五，对完整的方法进行了总结

1.从一个beta分布到一个可优化的离散评级分布

​ 我们将传统的beta分布进行扩展，然后将这个分布进行离散化，将间隔分割成一个bin来实现，每个bin代表了一个评估值的概率质量

​ \(W_{i,j,r}\)参数表示评级为r的bin宽度，所以\(\sum_{r=1}^nW_{i,j,r}=1\)

\(R_r\)的底部边缘可以被定义为\(E_r=E_{r-1}+(R^{max}-R^{min})W_{i,j,r-1}\)

并且\(E_1=R^{min}\)是第一个边缘。评级的概率就是PDF下和相应bin内的概率

​ 总之，后面是一串离散化的方法，离散过程的示意图为：

​ 然后，通过一系列分析，得到离散评级是完全可微的输入参数。因为可以很容易的使用它来优化交叉熵损失

2.建模的平均值和置信度

​ 之前的方法是从参数\(\alpha_{i,j}\)和\(\beta_{i,j}\)中生成评级的\(R_{i,j}\)的离散评级分布。这部分是提出基于用户和项目嵌入之间的交互来生成\(\alpha_{i,j}\)和\(\beta_{i,j}\)的方法

​ 我们引入平均值\(\mu_{ij}\in(0,1)\)和置信度\(v_{ij}\)，使其作为beta分布的平均值和样本量，前面对beta分布进行了参数化，\(\mu=\alpha/(\alpha+\beta)\)，\(v=\alpha+\beta\)。所以通过平均值和置信度就可以求出\(\alpha_{ij}\)和\(\beta_{ij}\)。然后受MF的简单性的启发，我们为每个项目V和每个用户U引入一个非0学习嵌入，平均值\(\mu\)可以用余弦相似度进行建模

​ 嵌入方向之间的相似度越高，预测的评级分布的平均值就越高。然后一个想法就是，从嵌入到正标量的任何可微转换都可以用于置信度。以下是三种转换方式：

​ 第一种方式下更大嵌入量的用户或项目会导致更自信的预测。虽然它简单容易理解，但是它缺乏表达能力，并且不能捕获因为特定用户-项目之间更复杂的交互

​ 第二种方式下，嵌入的方向和距离都决定了结果的置信度，因此这个模型可以捕捉到用户和项目之间更复杂的交互，但是也更难理解

​ 第三种方式下，由于使用了绝对值，高相似性和不相似性都会导致高置信度的预测。有明显缺点，个人感觉最好不采取

​ 我们的新方法只使用用户嵌入和项目嵌入，与MF具有相同的模型复杂性，但是LBD将预测建模为概率分布

3.建模用户和项目偏差

​ 因为MF包括用户和项目的偏差权重，并且这些权重对MF很有效，所以我们将其添加到LBD模型中

​ 我们引入可优化的标量a,b。其中\(a_0\)表示全局权重，\(a_1\)表示用户权重，\(a_j\)表示项目权重。b也类似。然后我们将这些偏差权重添加到通过嵌入预测的权重中

​

​ 其中\(\epsilon\)是一个非常小的正量，确保\(\alpha\)和\(\beta\)都大于0

​ 但是该优化只考虑了最终的分布。因此它并没有直接优化鲜先验分解和似然分解的准确性。

​ 然后提出了在替代参数化方面的偏差权重

​ 显然，\(v\)越大，置信度越大，\(u\)越大，平均值越小

建模静态和自适应离散化策略

​ 提出了一种静态的分箱策略来建模W：LBD-S，以及自适应的装箱策略：LBD-A

​ LBD-S的静态策略直接使每个箱子均衡。对于\(\forall i,j,r:W_{i,j,r}=\frac{1}{n}\)。该策略假设偏好和评级之间存在线性关系。但是这个假设是不正确的，比如在评分方面，用户更倾向于选择整数评分而不是小数评分，不能反映潜在偏好的实际聚类

​ 而自适应分箱策略可以改变每个评级、用户和项目的分箱宽度，从而可以更好的捕捉某些评级值的频率差异。

​ 我们引入非归一化分箱宽度\(w_{i,j,r}=exp(\theta_i^r+\theta_j^r)\)。然后对其进行归一化\(W_{i,j,r}=w_{i,j,r}\sum_{r'=1}^nw_{i,j,r'}\)。通过增加某些评级值相对于其他评级值的箱子宽度，这些评级值可以变得更有可能，而不改变潜在的beta分布。

​ 因此，LBD-A可以捕获LBD-S无法捕获的非平滑模式。

LBD方法的概述

​ LBD对每个用户和项目都有一个可优化的嵌入向量。这些向量之间的余弦相似度决定了平均预测，并且通过一个正函数得到一个表示预测的置信度。然后将平均值和置信度映射到\(\alpha\)和\(\beta\)项，并且添加偏差项。所得到的值可作为beta分布的输入参数。这个beta分布是对具有明确不确定性的用户偏好的预测；偏好被建模为区间[0,1]中的比率，而beta PDF\(f_B\)表示每个可能值的预测有多可能。然后将这个分布进行转换以匹配可能的评级值的范围，并离散以给出每个评级的精确概率。离散化既可以使用相同大小的箱子来完成，也可以通过根据用户和项目的项（